A posteriori error estimation for the non-self-consistent Kohn–Sham equations
Abstract
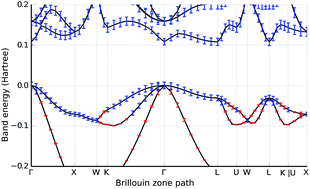
We address the problem of rigorously bounding the errors in the numerical solution of the Kohn–Sham equations due to (i) the finiteness of the basis set, (ii) the convergence thresholds in iterative procedures, and (iii) the propagation of rounding errors in floating-point arithmetic. In this contribution, we compute fully-guaranteed bounds on the solution of the non-self-consistent equations in the pseudopotential approximation in a plane-wave basis set. We demonstrate our methodology by providing band structure diagrams of silicon annotated with error bars indicating the combined error.
- This article is part of the themed collection: New horizons in density functional theory


 Please wait while we load your content...
Please wait while we load your content...