Exchange couplings and quantum phases in two dissimilar arrays of similar copper dinuclear units

Abstract

To investigate the magnetic properties and the spin entanglement of dinuclear arrays, we prepared compounds [{Cu(pAB)(phen)H₂O}₂·NO₃·pABH·2H₂O], 1, and [Cu₂(pAB)₂(phen)₂pz]_n, 2 (pABH = p-aminobenzoic acid, phen = 1,10-phenanthroline and pz = pyrazine). The structure of 1 is known and we report here that of 2. They contain similar dinuclear units of Cu^II ions with 1/2-spins S₁ and S₂ bridged by pairs of pAB molecules, with similar intradinuclear exchange 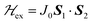and fine interactions 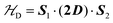, but different 3D crystal arrays with weak interdinuclear exchange J′, stronger in 2 than in 1. To investigate the magnetic properties and the spin entanglement produced by J′, we collected the powder spectra of 1 and 2 at 9.4 GHz and T between 5 and 298 K, and at 34.4 GHz and T = 298 K and single-crystal spectra at room T and 34.4 GHz as a function of magnetic field (B₀) orientation in three crystal planes, calculating intradinuclear magnetic parameters J⁽¹⁾₀ = (−75 ± 1) cm⁻¹, J⁽²⁾₀ = (−78 ± 2) cm⁻¹, |D⁽¹⁾| = (0.142 ± 0.006) cm⁻¹, |D⁽²⁾| = (0.141 ± 0.006) cm⁻¹ and E⁽¹⁾ ∼ E⁽²⁾ ∼ 0. Single crystal data indicate a quantum entangled phase in 2 around the crossing between two fine structure EPR absorption peaks within the spin triplet. This phase also shows up in powder samples of 2 as a U-peak collecting the signals of the entangled microcrystals, a feature that allows estimating |J′|. Transitions between the two quantum phases are observed in single crystals of 2 changing the orientation of B₀. We estimate interdinuclear exchange couplings |J′⁽¹⁾| < 0.003 cm⁻¹ and |J′⁽²⁾| = (0.013 ± 0.005) cm⁻¹, in 1 and 2, respectively. Our analysis indicates that the standard approximation of a spin Hamiltonian with S = 1 for the dinuclear spectra is valid only when the interdinuclear coupling is large enough, as for compound 2 (|J′⁽²⁾/J⁽²⁾₀| ∼ 1.7 × 10⁻⁴). When J′ is negligible as in 1, the real spin Hamiltonian with two spins 1/2 has to be used. Broken-symmetry DFT predicts correctly the nature and magnitude of the antiferromagnetic exchange coupling in 1 and 2 and ferromagnetic interdinuclear coupling for compound 2.