Criticality in elastoplastic models of amorphous solids with stress-dependent yielding rates
Abstract
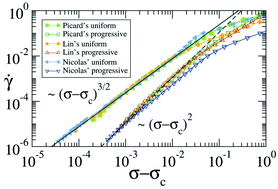
We analyze the behavior of different elastoplastic models approaching the yielding transition. We propose two kinds of rules for the local yielding events: yielding occurs above the local threshold either at a constant rate or with a rate that increases as the square root of the stress excess. We establish a family of “static” universal critical exponents which do not depend on this dynamic detail of the model rules: in particular, the exponents for the avalanche size distribution P(S) ∼ S−τSf(S/Ldf) and the exponents describing the density of sites at the verge of yielding, which we find to be of the form P(x) ≃ P(0) + xθ with P(0) ∼ L−a controlling the extremal statistics. On the other hand, we discuss “dynamical” exponents that are sensitive to the local yielding rule. We find that, apart form the dynamical exponent z controlling the duration of avalanches, also the flowcurve's (inverse) Herschel–Bulkley exponent β (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ (σ − σc)β) enters in this category, and is seen to differ in ½ between the two yielding rate cases. We give analytical support to this numerical observation by calculating the exponent variation in the Hébraud–Lequeux model and finding an identical shift. We further discuss an alternative mean-field approximation to yielding only based on the so-called Hurst exponent of the accumulated mechanical noise signal, which gives good predictions for the exponents extracted from simulations of fully spatial models.
∼ (σ − σc)β) enters in this category, and is seen to differ in ½ between the two yielding rate cases. We give analytical support to this numerical observation by calculating the exponent variation in the Hébraud–Lequeux model and finding an identical shift. We further discuss an alternative mean-field approximation to yielding only based on the so-called Hurst exponent of the accumulated mechanical noise signal, which gives good predictions for the exponents extracted from simulations of fully spatial models.


 Please wait while we load your content...
Please wait while we load your content...