Arrested dynamics of the dipolar hard sphere model
Abstract
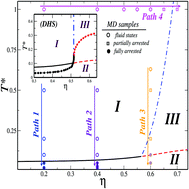
We report the combined results of molecular dynamics simulations and theoretical calculations concerning various dynamical arrest transitions in a model system representing a dipolar fluid, namely, N (soft core) rigid spheres interacting through a truncated dipole–dipole potential. By exploring different regimes of concentration and temperature, we find three distinct scenarios for the slowing down of the dynamics of the translational and orientational degrees of freedom: at low (η = 0.2) and intermediate (η = 0.4) volume fractions, both dynamics are strongly coupled and become simultaneously arrested upon cooling. At high concentrations (η ≥ 0.6), the translational dynamics shows the features of an ordinary glass transition, either by compressing or cooling down the system, but with the orientations remaining ergodic, thus indicating the existence of partially arrested states. In this density regime, but at lower temperatures, the relaxation of the orientational dynamics also freezes. The physical scenario provided by the simulations is discussed and compared against results obtained with the self-consistent generalized Langevin equation theory, and both provide a consistent description of the dynamical arrest transitions in the system. Our results are summarized in an arrested states diagram which qualitatively organizes the simulation data and provides a generic picture of the glass transitions of a dipolar fluid.


 Please wait while we load your content...
Please wait while we load your content...