Three-dimensional yielding in anisotropic materials: validation of Hill's criterion

Abstract

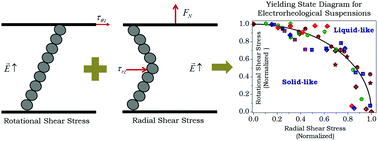
Yielding transition in isotropic soft materials under the superposition of orthogonal deformation fields is known to follow von Mises’ criterion. However, in anisotropic soft materials, von Mises’ criterion fails owing to the preferred directions associated with the system. In this work we study a model anisotropic yield stress system: electrorheological (ER) fluids which show structural formation in the direction of an electric field. We subject the ER fluids to the superposition of orthogonal stress fields which leads to different yield stress values. We obtain a yielding state diagram by plotting the normalized rotational shear stress against the normalized radial shear stress corresponding to a yield point for a given electric field. Remarkably, the state diagram validates the Hill yielding criterion, which is a general yielding criterion for materials with anisotropy along three orthogonal directions, originally developed for metallic systems. Validation of Hill's criterion suggests the universality of its application in anisotropic systems including conventional anisotropic soft materials having yield stress.