Effects of local rearrangement of magnetic particles on deformation in magneto-sensitive elastomers

Abstract

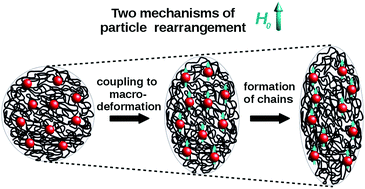
Based on the dipole–dipole approach for magnetic interactions we present a comprehensive analysis of spatial rearrangement of magnetic particles under a magnetic field and its effect on the magneto-induced deformation of magneto-sensitive elastomers. The presented formalism allows analyzing non-affine displacements of magnetic particles in a general way and reveals how the local rearrangement of particles under a magnetic field affects the magneto-induced deformation. The formalism includes two contributions: (1) displacements due to elastic coupling with a deformed matrix and (2) rearrangements on the background of the deformed matrix due to magnetic interactions between the particles. We show that in the linear response regime the sign of deformation is defined by the first contribution and the second one amplifies the magnitude of deformation. The sign and magnitude of deformation depend on the factors 〈cos² θ〉 and 〈cos⁴ θ〉, where averaging is over mutual pairs of particles and θ is the angle between the vector connecting the particles and the direction of the magnetic field. We test the new formalism on isotropic-like lattice distributions with 〈cos² θ〉 = 1/3 and show that the difference in the sign of their deformation is defined by the difference in the factor 〈cos⁴ θ〉. The results are compared for 3-dimensional and 2-dimensional systems, which are shown to have a similar behavior as a function of the aspect ratio of a sample.