Local loop opening in untangled ring polymer melts: a detailed “Feynman test” of models for the large scale structure

Abstract

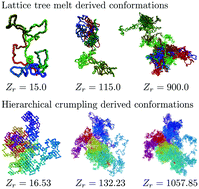
The conformational statistics of ring polymers in melts or dense solutions is strongly affected by their quenched microscopic topological state. The effect is particularly strong for untangled (i.e. non-concatenated and unknotted) rings, which are known to crumple and segregate. Here we study these systems using a computationally efficient multi-scale approach, where we combine massive simulations on the fiber level with the explicit construction of untangled ring melt configurations based on theoretical ideas for their large scale structure. We find (i) that topological constraints may be neglected on scales below the standard entanglement length, L_e, (ii) that rings with a size 1 ≤ L_r/L_e ≤ 30 exhibit nearly ideal lattice tree behavior characterized by primitive paths which are randomly branched on the entanglement scale, and (iii) that larger rings are compact with gyration radii 〈R_g²(L_r)〉 ∝ L_r^2/3. The detailed comparison between equilibrated and constructed ensembles allows us to perform a “Feynman test” of our understanding of untangled rings: can we convert ideas for the large scale ring structure into algorithms for constructing (nearly) equilibrated ring melt samples? We show that most structural observables are quantitatively reproduced by two different construction schemes: hierarchical crumpling and ring melts derived from the analogy to interacting branched polymers. However, the latter fail the “Feynman test” with respect to the magnetic radius, R_m, which we have defined based on an analogy to magnetostatics. While R_m is expected to vanish for double-folded structures, the observed values of 〈R_m²(L_r)〉 ∝ 〈R_g²(L_r)〉 provide a simple and computationally convenient measure of the presence of a non-negligible amount of local loop opening in crumpled rings.