Pattern selection when a layer buckles on a soft substrate†
Abstract
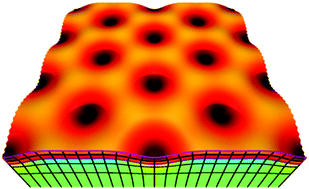
If a neo-Hookean elastic layer adhered to a neo-Hookean substrate grows equibiaxially, it will buckle into a topographic pattern. Here, we combine higher order perturbation theory and finite element numerics to predict the pattern formed just beyond the buckling threshold. More precisely, we construct a series of solutions corresponding to hexagonal, square and stripe patterns, and expand the elastic energy for each pattern as a Landau-like energy series in the topography amplitude. We see that, for square and stripe patterns, the elastic energy is invariant under topography inversion, making the instabilities supercritical. However, since patterns of hexagonal dents are physically different to patterns of hexagonal bumps, the hexagonal energy lacks this invariance. This lack introduces a cubic term which causes hexagonal patterns to be formed subcritically and are hence energetically favoured. Our analytic calculation of the cubic term allows us to determine that dents are favoured in incompressible systems, but bumps are favored in sufficiently compressible systems. Finally, we consider a stiff layer sandwiched between an identical substrate and superstrate pair. This system has topography inversion symmetry, so hexagons form supercritically, and square patterns are favoured. We use finite element calculations to verify our theoretical predictions for each pattern, and confirm which pattern is selected. Previous work has used a simplified elastic model (a plate & a linear elastic substrate) that possesses invariance under topography inversion, and hence incorrectly predicted square patterns. Our work demonstrates that large strain geometry is sufficient to break this symmetry and explain the hexagonal dent patterns observed in buckling experiments.


 Please wait while we load your content...
Please wait while we load your content...