Identification of optimally stable nanocluster geometries via mathematical optimization and density-functional theory†
Abstract
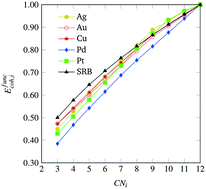
Small nanoparticles, a.k.a. nanoclusters, of transition metals have been studied extensively for a wide range of applications due to their highly tunable properties dependent on size, structure, and composition. For these small particles, there has been considerable effort towards theoretically predicting what is the most energetically favorable arrangement of atoms when forming a nanocluster. In this work, we develop a computational framework that couples density-functional theory calculations with mathematical optimization modeling to identify highly stable, mono-metallic transition metal nanoclusters of various sizes. This is accomplished by devising and solving a rigorous mathematical optimization model that maximizes a general cohesive energy function to obtain nanocluster structures of provably maximal cohesiveness. We then utilize density-functional theory calculations and error term regression to identify model corrections that are necessary to account with better accuracy for different transition metals. This allows us to encode metal-specific, analytical functions for cohesive energy into a mathematical optimization-based framework that can accurately predict which nanocluster geometries will be most cohesive according to density-functional theory calculations. We employ our framework in the context of Ag, Au, Cu, Pd and Pt, and we present sequences of highly cohesive nanoclusters for sizes up to 100 atoms, yielding insights into structures that might be experimentally accessible and/or structures that could be used as model nanoclusters for further study.
- This article is part of the themed collection: MSDE Emerging Investigators 2020


 Please wait while we load your content...
Please wait while we load your content...
