Kinetic energy densities based on the fourth order gradient expansion: performance in different classes of materials and improvement via machine learning
Abstract
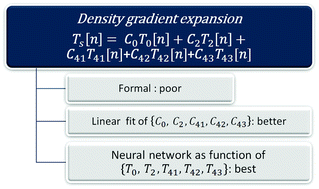
We study the performance of fourth-order gradient expansions of the kinetic energy density (KED) in semi-local kinetic energy functionals depending on the density-dependent variables. The formal fourth-order expansion is convergent for periodic systems and small molecules but does not improve over the second-order expansion (the Thomas–Fermi term plus one-ninth of the von Weizsäcker term). Linear fitting of the expansion coefficients somewhat improves on the formal expansion. The tuning of the fourth order expansion coefficients allows for better reproducibility of the Kohn–Sham kinetic energy density than the tuning of the second-order expansion coefficients alone. The possibility of a much more accurate match with the Kohn–Sham kinetic energy density by using neural networks (NN) trained using the terms of the 4th order expansion as density-dependent variables is demonstrated. We obtain ultra-low fitting errors without overfitting of NN parameters. Small single hidden layer neural networks can provide good accuracy in separate KED fits of each compound, while for joint fitting of KEDs of multiple compounds multiple hidden layers were required to achieve good fit quality. The critical issue of data distribution is highlighted. We also show the critical role of pseudopotentials in the performance of the expansion, where in the case of a too rapid decay of the valence density at the nucleus with some pseudopotentials, numeric instabilities can arise.


 Please wait while we load your content...
Please wait while we load your content...