Twist renormalization in molecular crystals driven by geometric frustration

Abstract

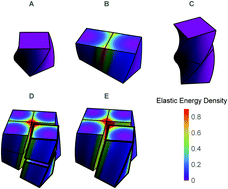
Symmetry considerations preclude the possibility of twist or continuous helical symmetry in bulk crystalline structures. However, as has been shown nearly a century ago, twisted molecular crystals are ubiquitous and can be formed by about 1/4 of organic substances. Despite its ubiquity, this phenomenon has so far not been satisfactorily explained. In this work we study twisted molecular crystals as geometrically frustrated assemblies. We model the molecular constituents as uniaxially twisted cubes and examine their crystalline assembly. We exploit a renormalization group (RG) approach to follow the growth of the rod-like twisted crystals these constituents produce, inquiring in every step into the evolution of their morphology, response functions and residual energy. The gradual untwisting of the rod-like frustrated crystals predicted by the RG approach is verified experimentally using silicone rubber models of similar geometry. Our theory provides a mechanism for the conveyance of twist across length-scales observed experimentally and reconciles the apparent paradox of a twisted single crystal as a finite size effect.