Cage dynamics leads to double relaxation of the intermediate scattering function in a binary colloidal system

Abstract

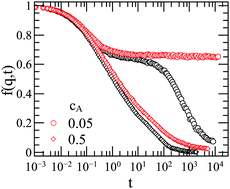
A system of binary colloids where one fraction of particles is aggregating by forming irreversible bonds and the other fraction of particles only interacts as hard spheres, is simulated using Brownian cluster dynamics. These aggregating species always formed percolating clusters for the case of diffusing hard spheres while for the static case, formation of percolating clusters depended on the fraction of static hard spheres in the system. The dynamics of the hard spheres inside the percolating clusters was studied by restarting the simulation after the kinetics of aggregation was arrested. Two cases were studied, one where the percolated particles moved within the bonds or cage dynamics was allowed and another where the movement within the bonds was not allowed or the cages were static. The hard spheres showed anomalous diffusion in both cases. The mean square displacement showed that for the case of dynamic cages we always had diffusive hard spheres irrespective of the fraction of hard spheres for volume fractions below 0.49. Static cages, depending on the fraction of hard spheres, showed either diffusive or arrested behavior of hard spheres. The intermediate scattering function of only the hard sphere particles showed double relaxation similar to the colloidal glass system for low volume fraction, where the fraction of hard sphere particles was small. For higher fractions we observed only a single stretched exponential. We could differentiate between slow and fast particles for both static and dynamic cages. For the case of static cages the hard spheres were permanently stuck inside the cages while for the case of dynamic cages almost all the hard spheres were moving in and out of the cages.