Complex crystalline structures in a two-dimensional core-softened system
Abstract
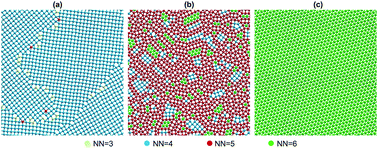
A transition from a square to a hexagonal lattice is studied in a 2D system of particles interacting via a core-softened potential. Due to the presence of two length scales of repulsion, different local configurations with four, five, and six neighbors are possible, leading to the formation of complex crystals. The previously proposed interpolation method is generalized to calculate pair correlations in crystals whose unit cell consists of more than one particle. The high efficiency of the method is illustrated using a snub square lattice as a representative example. Molecular dynamics simulations show that the snub square lattice is broken upon heating, generating a high-density quasicrystalline phase with 12-fold symmetry (HD12 phase). A simple theoretical model is proposed to explain the physical mechanism responsible for this phenomenon: with an increase in the density (from square to hexagonal phases), the concentrations of different local configurations randomly realized through a plane tiling change, which minimizes the energy of the system. The calculated phase diagram in the intermediate density range justifies the existence of the HD12 phase and demonstrates a cascade of first-order transitions “square – HD12 – hexagonal” solid phases with increasing density. The results allow us to better understand the physical mechanisms responsible for the formation of quasicrystals, and, therefore, should be of interest for broad community in materials science and soft matter.


 Please wait while we load your content...
Please wait while we load your content...