Nontrivial topology and topological phase transition in two-dimensional monolayer Tl†
Abstract
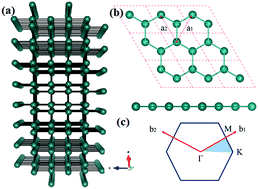
Topological insulating material with dissipationless edge states is a rising star in spintronics. While most two-dimensional (2D) topological insulators belong to group-IV or -V elements in a honeycomb lattice, herein, we propose a new topological phase in the 2D hexagonal group-III crystal, h-Tl, based on a tight-binding model and density-functional theory calculation. Analysis of band dispersion reveals a Dirac nodal-ring near the Fermi level, which is attributed to px,y/pz band crossing. Upon inclusion of spin–orbit coupling (SOC), h-Tl turns into a quantum spin Hall insulator under 21% biaxial strain, confirmed by integrating spin Berry curvature in the Brillouin zone and spin-polarized edge states. A prominent feature of its electronic properties is that the effect of SOC plays two essential roles of both topological gap opening and band inversion between px,y/pz orbitals, which is the first observed phenomenon in 2D materials. This study extends the scope of 2D elemental topological insulators and presents a platform to design new 2D topotronics materials.


 Please wait while we load your content...
Please wait while we load your content...