The curved kinetic boundary layer of active matter
Abstract
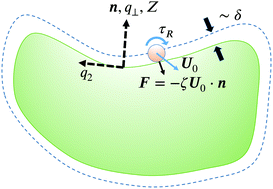
A body submerged in active matter feels the swim pressure through a kinetic accumulation boundary layer on its surface. The boundary layer results from a balance between translational diffusion and advective swimming and occurs on the microscopic length scale 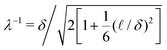 . Here
. Here 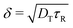 , DT is the Brownian translational diffusivity, τR is the reorientation time and
, DT is the Brownian translational diffusivity, τR is the reorientation time and 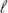 = U0τR is the swimmer's run length, with U0 the swim speed [Yan and Brady, J. Fluid. Mech., 2015, 785, R1]. In this work we analyze the swim pressure on arbitrary shaped bodies by including the effect of local shape curvature in the kinetic boundary layer. When δ ≪ L and
= U0τR is the swimmer's run length, with U0 the swim speed [Yan and Brady, J. Fluid. Mech., 2015, 785, R1]. In this work we analyze the swim pressure on arbitrary shaped bodies by including the effect of local shape curvature in the kinetic boundary layer. When δ ≪ L and 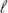 ≪ L, where L is the body size, the leading order effects of curvature on the swim pressure are found analytically to scale as JSλδ2/L, where JS is twice the (non-dimensional) mean curvature. Particle-tracking simulations and direct solutions to the Smoluchowski equation governing the probability distribution of the active particles show that λδ2/L is a universal scaling parameter not limited to the regime δ,
≪ L, where L is the body size, the leading order effects of curvature on the swim pressure are found analytically to scale as JSλδ2/L, where JS is twice the (non-dimensional) mean curvature. Particle-tracking simulations and direct solutions to the Smoluchowski equation governing the probability distribution of the active particles show that λδ2/L is a universal scaling parameter not limited to the regime δ,  ≪ L. The net force exerted on the body by the swimmers is found to scale as Fnet/(n∞ksTsL2) = f(λδ2/L), where f(x) is a dimensionless function that is quadratic when x ≪ 1 and linear when x ∼ 1. Here, ksTs= ζU02τR/6 defines the ‘activity’ of the swimmers, with ζ the drag coefficient, and n∞ is the uniform number density of swimmers far from the body. We discuss the connection of this boundary layer to continuum mechanical descriptions of active matter and briefly present how to include hydrodynamics into this purely kinetic study.
≪ L. The net force exerted on the body by the swimmers is found to scale as Fnet/(n∞ksTsL2) = f(λδ2/L), where f(x) is a dimensionless function that is quadratic when x ≪ 1 and linear when x ∼ 1. Here, ksTs= ζU02τR/6 defines the ‘activity’ of the swimmers, with ζ the drag coefficient, and n∞ is the uniform number density of swimmers far from the body. We discuss the connection of this boundary layer to continuum mechanical descriptions of active matter and briefly present how to include hydrodynamics into this purely kinetic study.


 Please wait while we load your content...
Please wait while we load your content...