Charged interfaces: electrochemical and mechanical effects†
Abstract
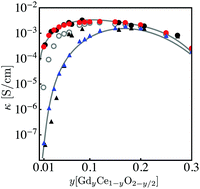
We establish a comprehensive space-charge treatment that includes electrochemomechanical effects to physically describe the equilibrium and transport properties of charged interfaces in ion-conducting solids. The theory is consistent with the laws of thermodynamics and Maxwell's equations and naturally includes the free energy contributions of the chemical, electrical, and mechanical fields at and in the vicinity of homo- and heterointerfaces. In the dilute limit, and in the absence of chemomechanical stresses, the theory reduces to the classic, well-established Gouy–Chapman description. In the strong substitution limit, the model naturally predicts the appearance of a Mott–Schottky-type layer and reproduces the well known experimentally observed behavior, including grain boundary solute segregation. We demonstrate the validity of this theory for polycrystalline GdyCe1−yO2−y/2, GCO. In the low substitution limit, electrochemical and chemomechanically-induced stresses favor the segregation of 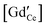 which locally expands the crystalline lattice, and thus promotes the formation of a wide depletion zone of oxygen vacancies in front of the interface, negatively impacting the macroscopic ionic conductivity. For high gadolinia substitution, interface segregation induces compressive stresses of 45 to 700 MPa and a weakly tensile region in the vicinity of the GCO homointerface, as a result of coupled, long range, electrochemomechanical interactions. The accumulation of gadolinium defects at the grain boundary locks-in oxygen vacancies, which in turn suppresses the depletion zone from the extended immediate neighborhood and decreases its macroscopic ionic conductivity. This is the first model where the grain boundary core explicitly includes chemomechanical effects.
which locally expands the crystalline lattice, and thus promotes the formation of a wide depletion zone of oxygen vacancies in front of the interface, negatively impacting the macroscopic ionic conductivity. For high gadolinia substitution, interface segregation induces compressive stresses of 45 to 700 MPa and a weakly tensile region in the vicinity of the GCO homointerface, as a result of coupled, long range, electrochemomechanical interactions. The accumulation of gadolinium defects at the grain boundary locks-in oxygen vacancies, which in turn suppresses the depletion zone from the extended immediate neighborhood and decreases its macroscopic ionic conductivity. This is the first model where the grain boundary core explicitly includes chemomechanical effects.


 Please wait while we load your content...
Please wait while we load your content...