The construction and application of Markov state models for colloidal self-assembly process control
Abstract
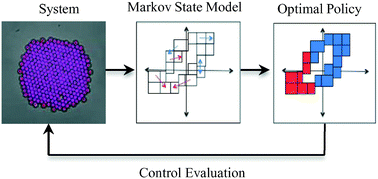
Markov state models have been widely applied to study time sequential events in a variety of disciplines. Due to their versatility for representing system stochasticity, Markov state models hold the promise to simplify simulation and design control policies for colloidal self-assembly systems. In this manuscript, we investigate the effects of state discretization, transition time, sampling approach, and the number of samples on the accuracy of a Markov state model for a colloidal self-assembly process. The model accuracy is evaluated based on the performance of the optimal control policy, calculated with a Markov decision process-based optimization framework, for controlling a Brownian dynamics simulation to produce perfect crystals. The results suggest using a dynamic sampling, a transition time similar to the system characteristic time, a clustering-based state discretization, and an average of at least five samples per state, to efficiently build an accurate Markov state model.


 Please wait while we load your content...
Please wait while we load your content...