Integer, fractional, and anomalous quantum Hall effects explained with Eyring's rate process theory and free volume concept

Abstract

The Hall effects, especially the integer, fractional and anomalous quantum Hall effects, have been addressed using Eyring's rate process theory and free volume concept. The basic assumptions are that the conduction process is a common rate controlled “reaction” process that can be described with Eyring's absolute rate process theory; the mobility of electrons should be dependent on the free volume available for conduction electrons. The obtained Hall conductivity is clearly quantized as 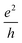with prefactors related to both the magnetic flux quantum number and the magnetic quantum number via the azimuthal quantum number, with and without an externally applied magnetic field. This article focuses on two dimensional (2D) systems, but the approaches developed in this article can be extended to 3D systems.