Hydrodynamics of bilayer membranes with diffusing transmembrane proteins

Abstract

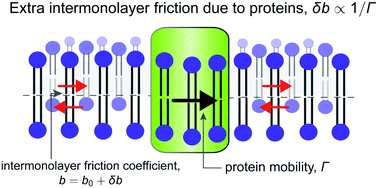
We consider the hydrodynamics of lipid bilayers containing transmembrane proteins of arbitrary shape. This biologically-motivated problem is relevant to the cell membrane, whose fluctuating dynamics play a key role in phenomena ranging from cell migration, intercellular transport, and cell communication. Using Onsager's variational principle, we derive the equations that govern the relaxation dynamics of the membrane shape, of the mass densities of the bilayer leaflets, and of the diffusing proteins' concentration. With our generic formalism, we obtain several results on membrane dynamics. We find that proteins that span the bilayer increase the intermonolayer friction coefficient. The renormalization, which can be significant, is in inverse proportion to the protein's mobility. Second, we find that asymmetric proteins couple to the membrane curvature and to the difference in monolayer densities. For practically all accessible membrane tensions (σ > 10⁻⁸ N m⁻¹) we show that the protein density is the slowest relaxing variable. Furthermore, its relaxation rate decreases at small wavelengths due to the coupling to curvature. We apply our formalism to the large-scale diffusion of a concentrated protein patch. We find that the diffusion profile is not self-similar, owing to the wavevector dependence of the effective diffusion coefficient.