Numerical density-to-potential inversions in time-dependent density functional theory

Abstract

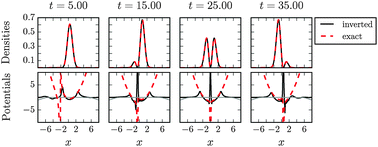
We treat the density-to-potential inverse problem of time-dependent density functional theory as an optimization problem with a partial differential equation constraint. The unknown potential is recovered from a target density by applying a multilevel optimization method controlled by error estimates. We employ a classical optimization routine using gradients efficiently computed by the discrete adjoint method. The inverted potential has both a real and imaginary part to reduce reflections at the boundaries and other numerical artifacts. We demonstrate this method on model one-dimensional systems. The method can be straightforwardly extended to a variety of numerical solvers of the time-dependent Kohn–Sham equations and to systems in higher dimensions.