Nano-scale surface wrinkling in chiral liquid crystals and plant-based plywoods

Abstract

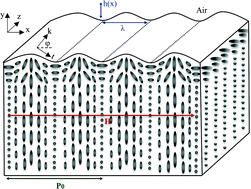
We present theoretical scaling and computational analysis of nanostructured free surfaces formed in chiral liquid crystals (LC) and plant-based twisted plywoods. A nemato-capillary model is used to derive a generalized equation that governs the shape of cholesteric free surfaces. It is shown that the shape equation includes three distinct contributions to the capillary pressure: area dilation, area rotation, and director curvature. To analyse the origin of periodic reliefs in plywood surfaces, these three pressure contributions and corresponding surface energies are systematically investigated. It is found that for weak homeotropic surface anchoring, the nano-wrinkling is driven by the director curvature pressure mechanism. Consequently, the model predicts that for a planar surface with a uniform tangential helix vector, no surface nano-scale wrinkling can be observed because the director curvature pressure is zero. Scaling is used to derive the explicit relation between the wrinkling's amplitude to the wavelength ratio as a function of the anisotropic surface tension, which is then validated with experimental values. These new findings can be used to characterize plant-based twisted plywoods, as well as to inspire the design of biomimetic chiro-optical devices.