The ICPMS signal as a Poisson process: a review of basic concepts†
Abstract
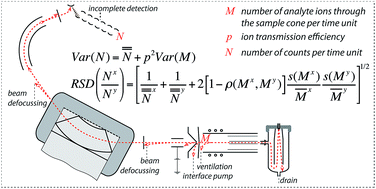
Understanding the structure of noise associated with a measurement process is interesting theoretically and has practical applications related to the quantification of detection capability, signal uncertainty and dead time. Here, we present and analyse arguments explaining the appearance of the Poisson process in the distribution of count numbers in inductively coupled plasma mass spectrometry (ICPMS) signals. We consider the Poisson distribution as a special case of the binomial distribution constrained by inefficient ion transmission from the ICP ion source to the detector. The universal form of the relevant Poisson process is doubly stochastic: the random nature of count numbers acquired per time unit is defined not only by the probabilistic selection of ions during their transport through the interface and ion channel, but also by fluctuations of the ion contents sampled by the spectrometer from the plasma and, more generally, by fluctuations of the rate of the Poisson process itself. Compared to an ordinary Poisson process, the doubly stochastic Poisson process has an excess variance that increases at higher analyte contents. The excess variance in the uncertainty of ICPMS signals is also known as flicker noise; it is an integral part of the doubly stochastic Poisson process and not a fully individual noise component. We review processes pertinent to its origin and formalisms used to describe it.

 Please wait while we load your content...
Please wait while we load your content...