Ligand field influence on the electronic and magnetic properties of quasi-linear two-coordinate iron(ii) complexes

Abstract

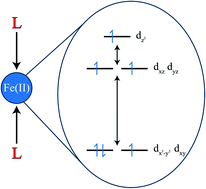
The 2 to 300 K magnetic susceptibilities of Fe{N(SiMe₂Ph)₂}₂, 1, Fe{N(SiMePh₂)₂}₂, 2, and the diaryl complex Fe(Ar^Pri₄)₂, 3, where Ar^Pri₄ is C₆H₃-2,6(C₆H₃-2,6-Prⁱ₂)₂ have been measured. Initial fits of these properties in the absence of an independent knowledge of their ligand field splitting have proven problematic. Ab initio calculations of the CASSCF/RASSI/SINGLE-ANISO type have indicated that the orbital energies of the complexes, as well as those of Fe(Ar^Me₆)₂, 4, where Ar^Me₆ is C₆H₃-2,6(C₆H₂-2,4,6-Me₃)₂), are in the order d_xy ≈ d_x²−y² < d_xz ≈ d_yz < d_z², and the iron(II) complexes in this ligand field have the (d_xy, d_x²−y²)³(d_xz, d_yz)²(d_z²)¹ ground electronic configuration with a substantial orbital contribution to their effective magnetic moments. An ab initio-derived ligand field and spin–orbit model is found to yield an excellent simulation of the observed magnetic properties of 1–3. The calculated ligand field strengths of these ligands are placed in the broader context of common coordination ligands in hypothetical two-coordinate linear iron(II) complexes. This yields the ordering I⁻ < H⁻ < Br⁻ ≈ PMe₃ < CH₃⁻ < Cl⁻ ≈ C(SiMe₃)₃⁻ < CN⁻ ≈ SAr^Pri₆− < Ar^Pri₄− < Ar^Me₆− ≈ N₃⁻ < NCS⁻ ≈ NCSe⁻ ≈ NCBH₃⁻ ≈ MeCN ≈ H₂O ≈ NH₃ < NO₃⁻ ≈ THF ≈ CO ≈ N(SiMe₂Ph)₂⁻ ≈ N(SiMePh₂)₂⁻ < F⁻ ≈ N(H)Ar^Pri₆− ≈ N(SiMe₃)Dipp⁻ < OAr^Pri₄−. The magnetic susceptibility of the bridged dimer, [Fe{N(SiMe₃)₂}₂]₂, 5, has also been measured between 2 and 300 K and a fit of χ_MT with the isotropic Heisenberg Hamiltonian, Ĥ = −2JŜ₁·Ŝ₂ yields an antiferromagnetic exchange coupling constant, J, of −131(2) cm⁻¹.