Trajectories of probe spheres in generalized linear viscoelastic complex fluids
Abstract
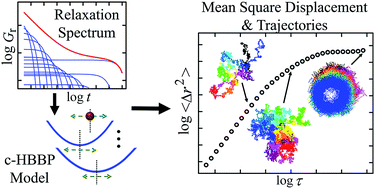
We have developed a fast simulation that generates a random walk of an isolated probe sphere in a generalized linear viscoelastic complex fluid over a highly extended dynamic range. We introduce a coupled harmonically bound Brownian particle (c-HBBP) model, in which the relaxation modes of the viscoelastic medium are treated as harmonic wells. These wells are coupled to the probe sphere and perform Brownian motion in bound harmonic potentials corresponding to the next-longer relaxation mode, according to the relaxation spectrum of the viscoelastic material. We implement this c-HBBP model by generating variable temporal step sizes that have a uniform distribution in logarithmic time. We create and analyze trajectories for several different viscoelastic complex fluids: a polymer system at its gel point, a dense emulsion system, a blend of two monodisperse polystyrene polymers for which the relaxation spectrum has been measured, and a model anisotropic soft system that shows dense emulsion-like and gel-point behaviors along two orthogonal directions. Except for unusual viscoelastic materials, such as the polymer system at its gel point, the generated trajectories are neither self-similar nor self-affine. The resulting mean square displacements predicted by the c-HBBP model are consistent with the single-particle generalized Stokes–Einstein relation of linear passive microrheology.

 Please wait while we load your content...
Please wait while we load your content...