Driving knots on DNA with AC/DC electric fields: topological friction and memory effects†
Abstract
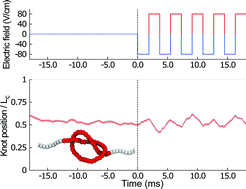
The dynamical properties of entangled polyelectrolytes are investigated theoretically and computationally for a proposed novel micromanipulation setup. Specifically, we investigate the effects of DC and AC electric fields acting longitudinally on knotted DNA chains, modelled as semiflexible chains of charged beads, under mechanical tension. We consider various experimentally accessible values of the field amplitude and frequency as well as several of the simplest knot types. In particular, we consider both torus and twist knots because they are respectively known to be able or unable to slide along macroscopic threads and ropes. Strikingly, this qualitative distinction disappears in this microscopic context because all the considered knot types acquire a systematic drift in the direction of the electric force. Notably, the knot drift velocity and diffusion coefficient in zero field (both measurable also experimentally) can be used to define a characteristic “frictional” lengthscale for the various knot types. This previously unexplored length provides valuable information on the extent of self-interactions in the nominal knotted region. It is finally observed that the motion of a knot can effectively follow the AC field only if the driving period is larger than the knot relaxation time (for which the self-diffusion time provides an upper bound). These results suggest that salient aspects of the intrinsic dynamics of knots in DNA chains could be probed experimentally by means of external, time-dependent electric fields.

 Please wait while we load your content...
Please wait while we load your content...