Optimal shapes and stresses of adherent cells on patterned substrates

Abstract

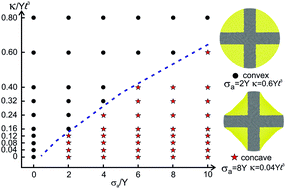
We investigate a continuum mechanical model for an adherent cell on two dimensional adhesive micropatterned substrates. The cell is modeled as an isotropic and homogeneous elastic material subject to uniform internal contractile stresses. The build-up of tension from cortical actin bundles at the cell periphery is incorporated by introducing an energy cost for bending the cell boundary, resulting in a resistance to changes in the local curvature. Integrin-based adhesions are modeled as harmonic springs that pin the cell to adhesive patches of a predefined geometry. Using Monte Carlo simulations and analytical techniques we investigate the competing effects of bulk contractility and cortical bending rigidity in regulating cell shapes on non-adherent regions. We show that the crossover from convex to concave cell edges is controlled by the interplay between contractile stresses and boundary bending rigidity. In particular, the cell boundary becomes concave beyond a critical value of the contractile stress that is proportional to the cortical bending rigidity. Furthermore, the intracellular stresses are found to be largely concentrated at the concave edge of the cell. The model can be used to generate a cell-shape phase diagram for each specific adhesion geometry.