A novel variable selection approach that iteratively optimizes variable space using weighted binary matrix sampling

Abstract

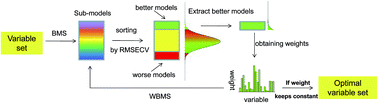
In this study, a new optimization algorithm called the Variable Iterative Space Shrinkage Approach (VISSA) that is based on the idea of model population analysis (MPA) is proposed for variable selection. Unlike most of the existing optimization methods for variable selection, VISSA statistically evaluates the performance of variable space in each step of optimization. Weighted binary matrix sampling (WBMS) is proposed to generate sub-models that span the variable subspace. Two rules are highlighted during the optimization procedure. First, the variable space shrinks in each step. Second, the new variable space outperforms the previous one. The second rule, which is rarely satisfied in most of the existing methods, is the core of the VISSA strategy. Compared with some promising variable selection methods such as competitive adaptive reweighted sampling (CARS), Monte Carlo uninformative variable elimination (MCUVE) and iteratively retaining informative variables (IRIV), VISSA showed better prediction ability for the calibration of NIR data. In addition, VISSA is user-friendly; only a few insensitive parameters are needed, and the program terminates automatically without any additional conditions. The Matlab codes for implementing VISSA are freely available on the website: https://sourceforge.net/projects/multivariate-analysis/files/VISSA/.