Low-energy non-linear excitations in sphere packings

Abstract

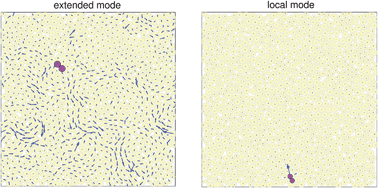
We study theoretically and numerically how hard frictionless particles in random packings can rearrange. We demonstrate the existence of two distinct unstable non-linear modes of rearrangement, both associated with the opening and the closing of contacts. The first mode, whose density is characterized by some exponent θ′, corresponds to motions of particles extending throughout the entire system. The second mode, whose density is characterized by an exponent θ ≠ θ′, corresponds to the local buckling of a few particles. Extended modes are shown to yield at a much higher rate than local modes when a stress is applied. 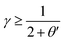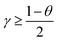We show that the distribution of contact forces follows P(f) ∼ f^{min(θ′,θ)}, and that imposing the restriction that the packing cannot be densified further leads to the bounds and , where γ characterizes the singularity of the pair distribution function g(r) at contact. These results extend the theoretical analysis of [Wyart, Phys. Rev. Lett., 2012, 109, 125502] where the existence of local modes was not considered. We perform numerics that support that these bounds are saturated with γ ≈ 0.38, θ ≈ 0.17 and θ′ ≈ 0.44. We measure systematically the stability of all such modes in packings, and confirm their marginal stability. The principle of marginal stability thus allows us to make clearcut predictions on the ensemble of configurations visited in these out-of-equilibrium systems, and on the contact forces and pair distribution functions. It also reveals the excitations that need to be included in a description of plasticity or flow near jamming, and suggests a new path to study two-level systems and soft spots in simple amorphous solids of repulsive particles.