Passive breakups of isolated drops and one-dimensional assemblies of drops in microfluidic geometries: experiments and models
Abstract
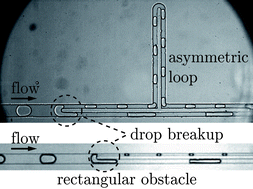
Using two different geometries, rectangular obstacles and asymmetric loops, we investigate the breakup dynamics of deformable objects, such as drops and bubbles, confined in microfluidic devices. We thoroughly study two distinct flow configurations that depend on whether object-to-object hydrodynamic interactions are allowed. When such interactions are introduced, we find that the volumes of the daughter objects created after breakup solely depend on the geometrical features of the devices and are not affected by the hydrodynamic and physicochemical variables; these results are in sharp contrast with those obtained for non-interacting objects. For both configurations, we provide simple phenomenological models that capture well the experimental findings and predict the evolution of the volumes of the daughter objects with the controlling dimensionless quantities that are identified. We introduce a mean-field approximation, which permits accounting for the interactions between objects during breakup and we discuss its conditions of validity.

 Please wait while we load your content...
Please wait while we load your content...