High accuracy geometric analysis of crystalline porous materials†
Abstract
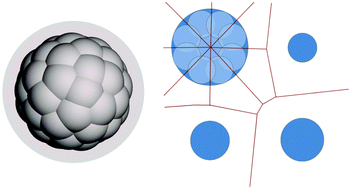
A number of algorithms to analyze crystalline porous materials and their porosities employ the Voronoi tessellation, whereby the space in the material is divided into irregular polyhedral cells that can be analyzed to determine the pore topology and structure. However, the Voronoi tessellation is only appropriate when atoms all have equal radii, and the natural generalization to structures with unequal radii leads to cells with curved boundaries, which are computationally expensive to compute. Therefore, high-throughput structure analysis codes utilize the radical Voronoi tessellation, which approximates the curved cells by polyhedra. In this study, we investigate the errors arising from this approximation reflected in the predicted values of two important porosity descriptors, the largest included and free sphere diameters. The maximum observed errors amount to ca. 0.6 Å for a test set comprised of

 Please wait while we load your content...
Please wait while we load your content...