Pore-size entropy of random hard-sphere packings
Abstract
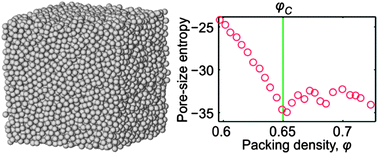
We introduce a method for calculating the entropy of random hard-sphere packings, also referred to as pore-size entropy. The method is applicable to packings of monodisperse or polydisperse spheres as well as non-spherical particles. Pore-size entropy allows us to analyze the packing microstructure and provides deep insight into the traditional concept of pore-size distribution. Specifically, the logarithm of the pore-size distribution's tail area is equal to the packing entropy. We reveal a local minimum in the plot of pore-size entropy vs. packing density (φ) for monodisperse frictionless sphere packings at a critical density of φC ≈ 0.65, independent of the employed packing generation protocol (Lubachevsky–Stillinger, Jodrey–Tory, and force-biased algorithms), which is a density with minimal number of available packing configurations. This entropy minimum is followed by an entropy increase as φ increases up to ∼0.68, corresponding to the emergence of crystalline structures in the coexistence region; beyond this packing density the entropy decreases again. In a complementary study we modify the Lubachevsky–Stillinger protocol and reproduce the random-close packing limit at φRCP ≈ 0.64. We conclude that φRCP ≈ 0.64 is the jamming point of the glassy states with the lowest density, whereas φC ≈ 0.65 is the jamming point of the densest glassy state (the ideal glass state).
 Please wait while we load your content...
Please wait while we load your content...