Baseline correction using adaptive iteratively reweighted penalized least squares
Abstract
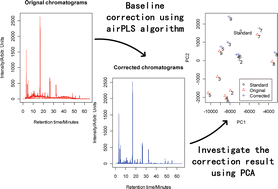
Baseline drift always blurs or even swamps signals and deteriorates analytical results, particularly in multivariate analysis. It is necessary to correct baseline drift to perform further data analysis. Simple or modified polynomial fitting has been found to be effective to some extent. However, this method requires user intervention and is prone to variability especially in low signal-to-noise ratio environments. A novel algorithm named adaptive iteratively reweighted Penalized Least Squares (airPLS) that does not require any user intervention and prior information, such as peak detection etc., is proposed in this work. The method works by iteratively changing weights of sum squares errors (SSE) between the fitted baseline and original signals, and the weights of the
- This article is part of the themed collection: 150th Anniversary Collection: Highly Cited Articles

 Please wait while we load your content...
Please wait while we load your content...