Diffusion of particles on a dice lattice with two nonequivalent sites
Abstract
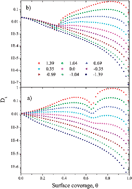
We investigated the diffusion of particles on a dice lattice with two kinds of nonequivalent sites. It is shown that the character of the particle migration depends crucially on the relative rates of the jumps from deep and shallow sites. The site inhomogeneity imposes specific pair correlation between the successive jumps. A general analytical expression for the chemical diffusion coefficient has been derived in the case of strong inhomogeneity. We have calculated coverage dependencies of the diffusion coefficients and some thermodynamic quantities for the different values of the lateral pairwise interaction between the particles. The analytical data have been compared with the numerical data obtained by the kinetic Monte Carlo simulations. Almost perfect agreement between the respective results has been found.

 Please wait while we load your content...
Please wait while we load your content...