Transient forces in flowing soft matter

Abstract

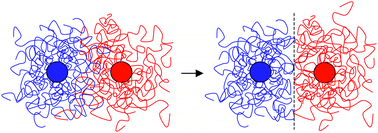
The dynamics of complex fluids often comprises motions of various components of the system on a broad range of time and length scales. Yet the low frequency linear and stationary non-linear rheology of such systems is basically concerned with displacements of centres of mass only. It is therefore just natural to try to develop simulation models that only keep track of the dynamics of the centres of mass of all diffusing constituents. All simulation models developed so far, however, have not been very successful mainly because they implicitly assume that a huge gap of time scales exists between the eliminated and simulated coordinates.

In this paper we propose a model, which keeps track of slow perturbations of the thermodynamic state of the eliminated coordinates induced with every displacement of the simulated coordinates. These perturbations give rise to non-equilibrium forces in addition to the usual thermodynamic forces deriving from the potential of mean force. Because these forces slowly fade away when the perturbations of the eliminated coordinates relax towards equilibrium, they are called transient forces. In the first part of the paper the model is presented in a most general way in order to provide a framework that can be applied to a broad range of soft matter systems. In the second part the general framework is further detailed in several applications to derive special models that have been applied with great success in recent years. One example is given of the elimination of external coordinates.