On the nature of liquid junction and membrane potentials
Abstract
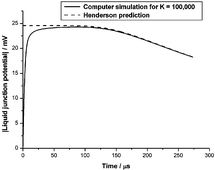
Whenever a spatially inhomogeneous electrolyte, composed of ions with different mobilities, is allowed to diffuse, charge separation and an electric potential difference is created. Such potential differences across very thin membranes (e.g. biomembranes) are often interpreted using the steady state Goldman equation, which is usually derived by assuming a spatially constant electric field. Through the fundamental Poisson equation of electrostatics, this implies the absence of free charge density that must provide the source of any such field. A similarly paradoxical situation is encountered for thick membranes (e.g. in ion-selective electrodes) for which the diffusion potential is normally interpreted using the Henderson equation. Standard derivations of the Henderson equation appeal to local electroneutrality, which is also incompatible with sources of electric fields, as these require separated charges. We analyse self-consistent solutions of the Nernst–Planck–Poisson equations for a 1 : 1-univalent electrolyte to show that the Goldman and Henderson steady-state membrane potentials are artefacts of extraneous charges created in the reservoirs of electrolyte solution on either side of the membrane, due to the unphysical nature of the usual (Dirichlet) boundary conditions assumed to apply at the membrane–electrolyte interfaces. We also show, with the aid of numerical simulations, that a transient electric potential difference develops in any confined, but initially non-uniform, electrolyte solution. This potential difference ultimately decays to zero in the real steady state of the electrolyte, which corresponds to thermodynamic equilibrium. We explain the surprising fact that such transient potential differences are well described by the Henderson equation by using a computer algebra system to extend previous steady-state singular perturbation theories to the time-dependent case. Our work therefore accounts for the success of the Henderson equation in analysing experimental liquid-junction potentials.

 Please wait while we load your content...
Please wait while we load your content...