Jumping solitary waves in an autonomous reaction–diffusion system with subcritical wave instability
Abstract
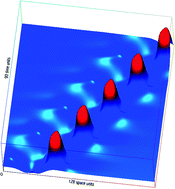
We describe a new type of solitary waves, which propagate in such a manner that the pulse periodically disappears from its original position and reemerges at a fixed distance. We find such jumping waves as solutions to a reaction–diffusion system with a subcritical short-wavelength instability. We demonstrate closely related solitary wave solutions in the quintic complex Ginzburg–Landau equation. We study the characteristics of and interactions between these solitary waves and the dynamics of related wave trains and standing waves.

 Please wait while we load your content...
Please wait while we load your content...