Open Access Article
Open Access ArticleHeterogeneous aging in a multi-cell lithium-ion battery system driven by manufacturing-induced variability in electrode microstructure: a physics-based simulation study
Parisa Akhtari
Zavareh
a,
Aditya Naveen
Matam
b and
Krishna
Shah
 *a
*a
aDepartment of Mechanical Engineering, The University of Alabama, Tuscasloosa, USA. E-mail: krishna.shah@ua.edu
bDepartment of Electrical and Computer Engineering, The University of Texas at Austin, USA
First published on 20th November 2025
Abstract
Heterogeneous aging of lithium-ion (Li-ion) battery cells within a battery pack is a major challenge that limits the pack's overall performance, safety, and life. Variations in cell degradation rates lead to nonuniform charge/discharge behavior among cells in a pack, accelerated aging in some cells turning them into “weak links”, and reducing energy throughput at the pack level. While previous studies have investigated uneven aging driven by differences in capacity or resistance, limited attention has been given to the root causes of these variations, particularly those arising from manufacturing-induced differences in the electrode microstructure. This study addresses this gap by investigating the effects of variations in the mean active material particle size across cells, a key design parameter of a porous electrode, on the aging behavior of these cells when connected in series and parallel. Using an electrochemical battery model, the aging behavior of individual cells and the pack as a whole is investigated for three electrical configurations (i.e., 1S4P, 4S1P, and 2S2P) at select C-rates and voltage windows. Results indicate that cells with smaller mean particle size degrade faster despite having a thinner SEI layer at the end of life, and even a minor variation of 1 µm in the mean active material particle size across cells can lead to significant uneven capacity fade across cells and accelerated aging of the pack, particularly at low C-rates. These findings highlight the critical impact that variability in the microstructure has on pack-level aging and provide insights into effective cell and pack manufacturing.
Introduction
Since their commercialization in the early 1990s, lithium-ion (Li-ion) batteries have gained popularity because of their excellent characteristics, including high-energy density, power density, and long cycle life.1–3 Initially utilized in personal electronics devices, their applications have expanded into transportation and industrial sectors, particularly for electric vehicles (EVs) and energy storage.3 A variety of cell chemistries have been proposed as promising candidates for these applications, each with distinct performance characteristics and limitations.3,4 Although Li-ion batteries have various advantages and are utilized in a wide range of applications, there remain challenges related to their material degradation, loss of performance due to aging, and safety issues.1,2,5 Aging and degradation are particularly important as they directly impact the battery's lifespan, charge/discharge performance, and safety.5,7 As batteries age, various degradation mechanisms may take place, including solid electrolyte interphase (SEI) layer growth, lithium (Li) plating, dendrite growth, and electrode material breakdown, ultimately leading to capacity fade, power loss, and reduction in roundtrip efficiency.6 Degradation in Li-ion batteries can lead to significant safety concerns, including fires, explosions, and system-level failures.2,5,6,21 For example, in 2025 the National Highway Traffic Safety Administration (NHTSA) documented a recall of approximately 19077 Nissan LEAF electric vehicles from the 2021–2022 model years because the Li-ion batteries may overheat during Level 3 fast charging, increasing the risk of fire and safety risk.34 In the safety recall report, Nissan noted that excessive lithium deposits inside battery cells could raise electrical resistance and lead to rapid heating, potentially causing a thermal runaway.34 Similarly, Tesla have reported multiple fire incidents involving Model S vehicles, which were attributed to battery module failures following high-energy impact or internal short-circuit events, highlighting the broader safety implications of battery degradation and failure mechanisms in Li-ion battery systems.8 Beyond safety concerns, battery degradation also poses economic and environmental challenges, as it necessitates more frequent replacements, increasing production and recycling burdens.1,3 The need for more frequent replacement of battery packs due to capacity fade and performance degradation leads to an increase in the overall cost of ownership for consumers and the manufacturer.35A large body of work is reported in the literature on Li-ion battery material degradation and aging.33,36–45 Experimental studies on Li-ion battery degradation have identified several mechanisms impacting battery performance.12–15,22–25 Metal oxide dissolution leads to capacity fade and increased cell polarization, as observed in past studies done through electrochemical testing.12 State of charge (SOC) and temperature affect calendar aging, while SOC swing, current, and temperature affect cycle aging.13 Investigation of Nickel–Manganese–Cobalt oxide (NMC)/graphite battery cells under various operating conditions using impedance spectroscopy and electrochemical analysis indicates an increase in solution and charge transfer resistance during cycling, with a high C-rate significantly promoting an increase in the resistance arising from diffusion.22 Electrochemical impedance spectroscopy and cycling tests conducted on commercial NMC Li-ion cells under a standardized real-world driving profile at 45 °C and 10 °C show an increase in capacity fade and internal resistance because of lithium loss and SEI formation.23
Impedance studies of NMC/graphite cells at 0 °C, 22 °C, and 45 °C under realistic automotive operating conditions with fast charging at 2C show a decrease in charge transfer resistance in initial aging stages at low temperatures that might be linked to increased double-layer capacitance.24 Also, at low temperatures (e.g., at 0 °C), an increase in the peak power is reported, indicating the complex role of temperature in aging.24 Elevated temperatures and upper cut-off voltages lead to increased rate of SEI growth and cell impedance, resulting in accelerated aging, as confirmed by electrochemical methods, X-ray diffraction (XRD), and prompt-gamma-activation-analysis (PGAA).25 In silicon-doped graphite and NCA cathode cells, post-mortem analysis and electrochemical testing indicate that depth-of-discharge significantly affects cycle life.14 Lower charging rates can accelerate aging under certain conditions, such as when the battery is charged to a high SOC during cycling. This is exacerbated at elevated temperatures (e.g., 60 °C) and highdepth of discharge.14 Trippetta et al.15 used a combination of cross-sectional scanning electron microscopy (SEM), nuclear magnetic resonance (NMR), and electrochemical measurements to study heterogeneous aging in high-energy Li-ion batteries with silicon–graphite composite negative electrode, revealing uneven degradation across different cell areas.15
Numerical studies have complemented experimental work by providing deeper insight into the degradation mechanisms of Li-ion batteries.15–17 To better understand the aging behavior of active materials, physics-based models have been developed to interpret quasi-OCV data.15 Sordi et al.16 developed a physics-based pseudo-2D (P2D) model to study the effect of variation in model parameters, such as lithium inventory and reaction rates, on the deterioration of Li-ion batteries under different operating conditions, including temperature fluctuations. Zhang et al.17 created a 3D simulation model that captures the electrochemical, thermal, and mechanical interactions in cells, simulating spatially varying properties such as SOC and current density. Another study developed a semi-empirical model to study SEI growth during the battery formation and cycling, capturing the irreversible cell expansion, SEI growth, and multi-species reactions.49 This study highlights how SEI growth consumes cyclable lithium as well as increases impedance and irreversible expansion which reduces battery capacity.49 A porous electrode pseudo two-dimensional (P2D) was reformulated to include SEI growth as a side reaction to study battery degradation under eight driving cycles and six charging protocols.48 Lawder et al.48 found that regenerative braking can increase the usable energy in some cases, while it can also accelerate capacity fade in others.48 Additionally, they found a high C-rate and deeper depth of discharge causing increased SEI growth and capacity fade.48
A lithium plating-induced aging model was proposed by Yang et al.47 to predict the Li-plating degradation mechanism in the Li-ion battery. This study shows that the formation and growth of the SEI layer on the anode surface leads to a decrease in the anode porosity.47 This leads to an increase in the electrolyte potential gradients, which makes it easier for the metallic lithium (Li) to start plating on the anode particle surface.47 Another study developed a 2D physics-based model to investigate how design parameters, such as anode thickness, electrolyte conductivity, and tab placement, influence the Li plating risk in the pouch cell by incorporating the actual winding structure of the Li-ion cell.46 The study reveals that the inner layers of the anode are more prone to the Li-plating due to overpotential distribution. Moreover, the higher conductivity of electrolyte and Li-ion diffusion in the cathode enhances the risk of Li-plating, while higher anode diffusivity reduces the Li-plating risk.46
The battery systems in many applications, especially EVs, are composed of multiple modules connected in series, forming a battery pack.6,7,9 These modules consist of multiple Li-ion cells connected in series-parallel to fulfill the specific energy and power requirements of the battery-powered system of interest.9 This makes studying the aging of battery cells in battery packs of significant relevance. Specifically, uneven aging of battery cells in a battery pack poses a key challenge. The uneven aging of battery cells in a pack has implications on the performance, lifespan, and safety of the battery pack. As the large number of cells in a battery pack deteriorate at different rates, the resulting uneven aging can lead to imbalances in performance and charge/discharge capacity, which in turn affect the overall energy efficiency and lifespan of the battery pack.10,11 To maximize the performance and lifespan of the battery packs, it is crucial to fully understand and address the challenges that arise from uneven aging of the individual cells and ensure that the aging effects are evenly distributed among the cells within a pack.11 Despite extensive research on cell-level degradation, there remains a need for further investigation of degradation patterns of individual cells in battery packs, as uneven cell degradation can worsen overall battery pack performance.10
The uneven aging of Li-ion cells within the battery packs is attributed to cell-specific variations, system-level factors, and temperature gradients.9,10 Cell-specific variations include differences in impedance and capacity within a large batch of cells caused by manufacturing inconsistencies and impurities in raw materials.9,10 System-level factors include variations in contact resistance between cells, battery pack design, and cooling system.9,26,28 The imbalance in the current distribution across cells in a pack, which can also lead to overheating in some of the cells, is due to both system-level factors and cell-specific variations.9,10,18–20,26 Past studies have indicated that capacity variations among cells due to the variability in manufacturing result in imbalance in the current distribution within the battery pack.19,25–30,51 Wu et al.27 used two cells with different initial capacities in parallel connection and observed that the one with higher capacity carried a larger amount of current during constant current (CC) discharge. Similar findings were reported by J. Brand et al.,28 who investigated two cells with the same internal resistance but different capacities connected in parallel. They found the cell with smaller capacity undergoing faster changes in SOC, during both charging and discharging, compared to the one with higher capacity, resulting in differences in OCV.28 The magnitude of the current flowing through individual cells within a pack is also affected by differences in the internal resistance. Bruen et al.29 studied four cells with different internal resistances connected in parallel configurations and observed that the cells with lower resistance experienced higher currents. This uneven current distribution increases the risk of overloading cells with lower internal resistances, leading them to operate under higher currents and faster degradation compared to the ones with higher internal resistances. Another experimental study conducted on new Panasonic 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cells and a retired battery pack from a Mercedes-Benz Vito e-Cell revealed that the capacity and impedance variations among the cells due to manufacturing differences and operating conditions lead to uneven load distribution and accelerated aging.9 This study also revealed that aged packs exhibited significantly higher capacity and internal resistance variations across cells, which worsened with further cycling by as much as 100% with respect to the variation prior to cycling. The results from this study show that parallel-connected cells do not converge in state of health (SOH) but instead become more imbalanced over time.9 Moreover, the temperature gradients within the battery pack have been found to lead to uneven current distributions.9,20,26,30,31 A study applying forced temperature gradients to series-connected cells found that colder cells exhibited accelerated aging, which was linked to Li-plating.20 This temperature-induced uneven degradation was the primary cause of voltage drift within the module.20 Another study cycled three parallel-connected LFP cells with different insulation and observed that the cell with higher operating temperatures, due to the kind of insulation applied, experienced 25% higher currents compared to the one with the lower temperature. This uneven current distribution difference caused accelerated aging of the cell operating at higher temperatures and significant uneven aging at the system level.33 In addition to capacity and internal resistance, SOC variations among the cells can both result in and contribute to uneven current distribution and uneven aging at the pack level.31–33 Shi et al. observed an SOC difference of about 7% at the end of charging between two parallel-connected cells, which led to current through one of the cells become 60% higher than the expected value.32 This study revealed that the imbalanced current distribution, due to SOC variation, causes one cell to experience higher electrochemical aging stress, degrade faster, and lead to uneven aging of the parallel-connected cells.32
650 cells and a retired battery pack from a Mercedes-Benz Vito e-Cell revealed that the capacity and impedance variations among the cells due to manufacturing differences and operating conditions lead to uneven load distribution and accelerated aging.9 This study also revealed that aged packs exhibited significantly higher capacity and internal resistance variations across cells, which worsened with further cycling by as much as 100% with respect to the variation prior to cycling. The results from this study show that parallel-connected cells do not converge in state of health (SOH) but instead become more imbalanced over time.9 Moreover, the temperature gradients within the battery pack have been found to lead to uneven current distributions.9,20,26,30,31 A study applying forced temperature gradients to series-connected cells found that colder cells exhibited accelerated aging, which was linked to Li-plating.20 This temperature-induced uneven degradation was the primary cause of voltage drift within the module.20 Another study cycled three parallel-connected LFP cells with different insulation and observed that the cell with higher operating temperatures, due to the kind of insulation applied, experienced 25% higher currents compared to the one with the lower temperature. This uneven current distribution difference caused accelerated aging of the cell operating at higher temperatures and significant uneven aging at the system level.33 In addition to capacity and internal resistance, SOC variations among the cells can both result in and contribute to uneven current distribution and uneven aging at the pack level.31–33 Shi et al. observed an SOC difference of about 7% at the end of charging between two parallel-connected cells, which led to current through one of the cells become 60% higher than the expected value.32 This study revealed that the imbalanced current distribution, due to SOC variation, causes one cell to experience higher electrochemical aging stress, degrade faster, and lead to uneven aging of the parallel-connected cells.32
Previous studies have largely focused on cell aging and material degradation at the single-cell level. A relatively fewer studies have investigated uneven aging across cells in battery packs caused by cell-to-cell manufacturing variations, system-level interactions, and temperature gradients. The existing research on pack-level uneven aging due to manufacturing variability has largely focused on differences in cell capacity and internal resistance which are cell level implications of certain material and porous electrode scale manufacturing related variabilities. A critical knowledge gap remains in understanding how variations in intrinsic material properties and porous electrode design parameters, such as the particle radius of active materials, electrode porosity, and thickness of the electrodes, affect the onset and progression of uneven aging within a pack. Because specific manufacturing processes directly influence these physical and structural properties, evaluating their effects can help identify specific manufacturing steps that most strongly contribute to this type of variability-induced uneven aging.
The present study addresses this gap through physics-based simulations that examine how variations in the porous electrode design parameters influence aging variations among cells in a pack for three distinct pack configurations. Among the several design parameters, the mean active material particle size variation is chosen as a representative manifestation of manufacturing inconsistency for several key reasons. First, particle size directly determines the electroactive surface area available for interfacial reactions, making it an important parameter that influences SEI reaction and growth rate, which is the assumed dominant degradation mechanism in this work. Second, particle size dictates the diffusion length within active material particles, affecting the local lithium concentration in the particle phase and surface chemical potential, which in turn influence SEI reaction kinetics. Third, particle size distribution is highly sensitive to upstream manufacturing steps such as milling, slurry mixing, and calendaring, and thus represents a realistic and practically significant source of variability in commercial cell production. In contrast, large variations in porosity or electrode thickness would proportionally alter the nominal capacity of individual cells, and cells with significant capacity differences would typically not be used in forming packs. Finally, the role of particle-size heterogeneity across cells on pack-level aging dynamics remains largely unexplored, providing an opportunity to establish a clear cause–effect relationship between this microstructural variability and emergent uneven aging behavior.
Accordingly, in this study, we investigate particle-size-induced uneven aging across a range of operating conditions (i.e., C-rate, charge/discharge voltage window) and electrical configurations of Li-ion battery packs. We directly relate the magnitude of variation in the mean active material particle size across cells in the pack with the aging trajectory of individual cells, change in capacity spread across cells with cycling, and overall aging trajectory of the pack. We also perform in-depth analysis on the internal states of the individual cells to understand and explain their aging trajectories. Finally, we study how the change in capacity spread across cells with cycling and pack level aging rate scale with increase in the pack size. While we only consider SEI growth as the degradation mechanism in this work, we present a systematic approach and modeling framework that can be extended to include other degradation mechanisms as necessary. Thus, this work provides a foundation for future studies on additional sources of manufacturing variability and their influence on aging behavior governed by one or more degradation mechanisms.
Methodology
Mathematical framework
In this section, we detail the mathematical models that comprise a battery pack. The framework consists of the single-particle model (SPM) for each cell and an electrical model for the coupling of cells in series, parallel configurations. The SPM formulation also includes the SEI side reaction and the resulting growth of SEI on the anode surface, which is responsible for capacity fade and resistance increase.Single particle model
Lithium intercalation in the lithium cobalt oxide (LCO) cathode and graphite anode is modeled by SPM. Both electrodes are represented by a spherical active material particle each, where the particle size considered represents the mean active material particle size or mean diffusion length in the particle in each electrode. The SOC variation in the active material particles across the electrode thickness is assumed to be negligible. SPM also ignores the ion transport in the electrolyte phase which implies negligible potential loss in the electrolyte. Due to a relatively low computational footprint (in comparison to P2D and higher-order models), SPM is favorable for the simulation of battery packs due to the large number of differential algebraic equations (DAEs) that need to be solved. Further, SPM is suitable for performing a large number of Monte-Carlo runs necessary to obtain statistically relevant results.Cathode equations
The Fick's law of diffusion, as applied in eqn (1), is used to model the ion diffusion in the cathode active material particles, with a surface boundary condition that accounts for applied current density at the particle surface. | (1) |
Assuming equal transfer coefficients (αc = αa = 0.5), the difference of exponential terms in the Butler–Volmer equation, a well-known equation relating reaction current with overpotential, can be rewritten as a hyperbolic sine function as shown in eqn (2). Eqn (3) details the equation for exchange current density.50
 | (2) |
| j0,n = kp(csurf,p)0.5(cmax,p − csurf,p)0.5 | (3) |
Anode equations
Again, the Fick's law of diffusion is used to model the ion diffusion in the anode active material particles. The governing equations are largely like those of the cathode. Additional anode-side equations are coupled with SPM to model the growth of the SEI layer on the anode surface during the charge cycle. | (4) |
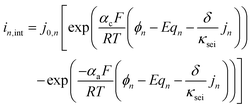 | (5) |
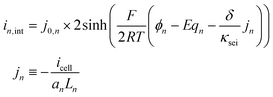 | (6) |
| j0,n = kn(csurf,n)0.5(cmax,n − csurf,n)0.5 | (7) |
The growth of the SEI layer is driven by a deviant side-current, is, that is a small fraction of the total applied current to the anode (eqn (8)). The relationship between the side-current and the anode surface chemical potential is given by the Tafel-like kinetics expression in eqn (9). To validate the SEI model implemented in this study, we compared its predictions with results from the multimodal physics-based aging model presented by Safari and Delacourt.50 The comparison confirms consistency in SEI growth behavior and capacity loss predicted by our simulation code with literature, and supporting figures are provided in the SI (Fig. S12).
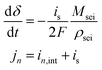 | (8) |
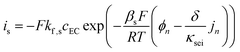 | (9) |
Electrical coupling of cells – pack formulation
For most applications, battery packs consist of cells that are interconnected in series and in parallel. This is done to increase operating voltage and capacity, respectively. Ubiquitous circuit laws are applied to establish the coupling between cell voltages and cell currents in a pack (Fig. 1). | ||
| Fig. 1 Schematic representation of a battery pack with an electrical configuration of (a) 1S4P, (b) 4S1P and (c) 2S2P. | ||
By Kirchhoff's current law in eqn (10), the local current on each parallel branch must sum to the total applied current to the pack:
 | (10) |
| icell,(i,1) = icell,(i,2) = ⋯ = icell,(i,N) = ibranch,(i) i ∈ {0, 1, …, M} | (11) |
As per Kirchhoff's voltage law, in eqn (12), the voltage drops across all parallel branches are set to be equal.
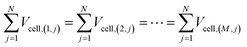 | (12) |
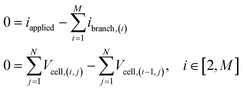 | (13) |
| Vcell = ϕp − ϕn |
Simulation methodology
In the current study, two approaches are used to assign variations in the electrode active material particle radius across the cells within the battery pack to investigate how manufacturing variations, specifically in the context of mean active material particle size, influence the aging characteristics of individual cells in a battery pack and the battery pack overall. In the first approach, the particle radius of each cell within the battery pack is picked by implementing a random sampling from a normal (Gaussian) distribution. The nominal particle radius of both positive and negative electrodes is 2 µm and three different target variabilities of 10%, 20%, and 30% with respect to the nominal particle size are applied. For each cell, a random value was assigned from the standard normal distribution using MATLAB's “randn” function, scaled by the introduced variation, and added to the nominal value of particle radius as give below:| Rn,i = Rn,0 (1 + σδi), δi ∼ N(0,1) | (14) |
The second approach aims to select the extreme particle radius values for each variation to investigate the worst-case scenario of uneven aging of the battery pack. In the second approach, the same nominal particle radius and standard deviation (SD) are used. However, instead of sampling randomly, the z-scores from controlled extreme ranges are assigned. Here, some cells are assigned a larger than nominal particle radius by choosing z-scores from the [2, 3] interval, corresponding to values 2 to 3 standard deviations above the mean. Meanwhile, values smaller than the nominal particle radius are assigned to the rest of the cells, and these values are selected from the z-score interval of [−3, −2], which included values 2 to 3 standard deviations below the mean. This combination of high and low extremes creates a battery pack with intentionally maximized variability, which is designed to exacerbate cell-to-cell variations and their effects on the aging of the battery pack. Since each battery pack comprises four cells, there are multiple possible combinations of large and small particle radii, including configurations with two large and two small, one large and three small, or one small and three large. The combination that produces the greatest degree of uneven aging among the cells was chosen. The chosen extreme combination varies based on the electrical configuration (i.e., 1S4P, 4S1P, or 2S2P). This study discusses the results obtained from the second approach in detail as it represents the worst-case scenario of cell-to-cell variation.
As explained in the preceding paragraphs, the particle radius variations in this study were randomly assigned for each simulation; as a result, a single run is insufficient to guarantee statistically reliable results. To ensure that the outcomes reflected robust trends rather than random fluctuations, simulations were repeated multiple times. After each set of runs, the SD, eqn (15), and standard error of mean (SEM), eqn (16), of the capacity across cells were calculated based on the following equations:
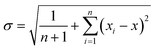 | (15) |
 | (16) |
Results and discussion
Using the modeling framework and simulation methodology discussed in the Methodology section, we investigated the effect of variation in the mean electrode active material particle size across a 4-cell Li-ion battery pack on the overall aging behavior of the pack as well as the individual cells in the pack. The mean active material particle size is referred simply as particle radius moving forward. We considered three different electrical configurations, namely 1S4P, 4S1P, and 2S2P, to understand how the type of interconnection among cells (i.e., series, parallel, and a combination of the two) may influence the complex interactions between cells. The results, in turn, would dictate the aging behavior and trajectory of the individual cells and the pack. The extent to which manufacturing variation in the particle radius affects the aging trajectory of the pack and the SD in the cell capacity across cells in the pack over the pack lifetime were studied for all configurations. Three manufacturing variation scenarios with three different standard deviations in the particle radius corresponding to 10%, 20%, and 30% of the base particle radius were considered.As 1S4P entails all cells operating at the same terminal voltage but drawing different currents, this configuration was studied at two different C-rates to determine how the magnitude of total current applied could influence the current distribution across cells, and as a result, the aging characteristics of the cells and the pack. Based on similar reasoning, in the case of 4S1P, two different voltage windows were analyzed. Two C-rates and voltage windows in the case of 2S2P configuration were considered, as this configuration can involve both voltage variation and current variation across cells.
All parallel electrical configuration – 1S4P
The first case study involved a battery pack with a 1S4P electrical configuration cycled at two C-rates, 0.1C and 1C, using the simulation methodology detailed previously. This case study was undertaken to understand how the variation in particle radii across cells operating at the same terminal voltage influences the current individual cells draw/deliver, and how that ultimately affects their aging behavior individually and collectively as a pack.As shown in Table 1, at the pack level, increasing the SD in the particle radius across cells significantly accelerated capacity fade. At 0.1C, the pack reached 80% of its initial capacity, referred to as end of life (EOL) in the present study, after approximately 2991, 1866, and 1119 cycles for the three standard deviations equaling 10%, 20%, and 30% of base particle radius, respectively. At 1C, the corresponding lifespans were found to be 4986, 3190, and 2601 cycles, respectively, demonstrating a similar effect of increasing SD in the particle radius across cells on the pack aging rate, albeit with overall higher cycle counts for reaching EOL compared to 0.1C. This general trend indicates that although intrinsic manufacturing variability introduces uneven aging potential, the external operating regime, particularly the C-rate in the case of parallel connected cells, plays an important role in determining system-level outcomes.
| Pack electrical configuration | Particle radius variation (%) | 2.75–4.2 V | 3.25–4 V | ||
|---|---|---|---|---|---|
| 0.1C | 1C | 0.1C | 1C | ||
| Cycle life | |||||
| 1S4P | 10 | 2991 | 4986 | NA* | |
| 20 | 1866 | 3190 | |||
| 30 | 1119 | 2601 | |||
| 4S1P | 10 | 2847 | NA* | 3918 | NA* |
| 20 | 2667 | 3510 | |||
| 30 | 1319 | 1401 | |||
| 2S2P | 10 | 2036 | 3079 | 2307 | 4007 |
| 20 | 1764 | 2919 | 1956 | 3592 | |
| 30 | 815 | 2021 | 832 | 1855 | |
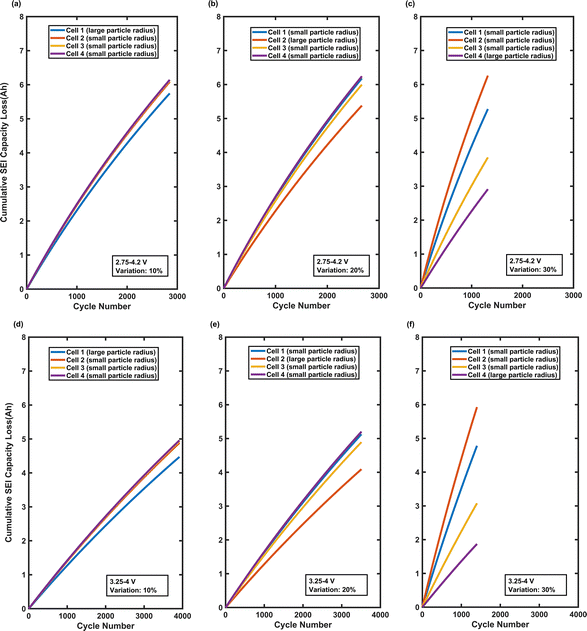
Fig. 2 shows a decline in the charge capacity of all four cells with cycling at two different C-rates for all three particle radius variations. For the 30% variation case at 0.1C, cell 4, with the smallest particle radius of 0.29 µm, exhibited a dramatic capacity loss of approximately 40% at EOL for the battery pack, while cells 1 and 3, with the largest particle radii of 3.49 µm and 3.77 µm, respectively, experienced only 9% capacity decay, approximately. For the 20% variation case, the cells with a smaller particle radius cell capacity degraded by around 24–26%, whereas the cells with a larger particle radius degraded only around 15%. Even at a 10% variation case, slight capacity differences emerged, with cells having smaller particles showing a marginally higher fade. Such patterns arise due to SEI growth being a surface-area-driven mechanism, disproportionately affecting the cells with higher specific surface area (i.e., cells with small active material particles), accelerating lithium consumption, leading to a faster capacity fade. According to Fig. S3, cells with larger particle radii, such as cell 1 for the 30% variation case, consistently develop thicker SEI layers because the SEI forms over a smaller surface area. However, this does not imply greater total SEI growth; in fact, smaller-particle cells experience more SEI growth overall due to their significantly larger surface area.
Importantly, when the capacity fade is normalized by the number of cycles, the calculated overall aging rates highlighted the severity of the capacity fade in small-particle cells compared to large-particle cells. For a 30% variation case at 0.1C, cell 4 degraded at an average rate of around 0.036% per cycle, nearly four times faster than large-particle cells 1 and 3, which degraded at around 0.008% per cycle. At 1C, the aging rates are markedly lower and more uniform across all cells, ranging between 0.006% and 0.010% per cycle, and the capacity of the individual cells appears to converge and their degradation rates are observed to become more even with cycling. This convergence indicated that the high kinetic demands of higher current rates during the cycling suppressed the manifestation of intrinsic manufacturing differences in terms of SEI based capacity loss, leading the cells to age more evenly over time.
Fig. 3 depicts the current deviation across cells by plotting scaled currents for all four cells, which are calculated by taking the ratio of actual cell current to the ideal, evenly distributed cell current. This figure provides detailed information on how current distribution evolves under different levels of variation and C-rate. At 0.1C, particularly at a higher level of variation (i.e., 30%), the system shows significant non-uniform current distribution. For instance, at 30% particle radii variation and EOL, cell 1 with a larger particle radius of 3.49 µm exhibited a scaled discharge current as high as 1.6, indicating it provided around 60% more current than its nominal ideal share at times. Cell 4, the one with the smallest particle radius of 0.29 µm, exhibited a scaled current as low as 0.6, which means a contribution of about 60% of the nominal ideal current at times. The same pattern is observed during charging as well, where the cells with a large particle radius reached scaled current as high as 1.4–1.6 at EOL, while the current share of cells with a small particle radius dropped to 0.6–0.8.
The evolution of anode potential over time, as shown in Fig. S1 and S2, provided additional insight into the aging behavior observed at the cell level, particularly during the charging phase, as that is when SEI formation occurrs. At 0.1C, cells with smaller particle radii exhibit a slight upward shift in anode potential by the EOL, indicating a higher interfacial resistance due to enhanced SEI growth. However, cells with larger particle radii maintain lower anode potential throughout cycling, which aligns with their lower degradation rates and lesser rate of SEI formation relative to smaller-particle cells. At 1C, the anode potential of cells with larger particle radii dropped more significantly during charging, even becoming negative relative to the Li/Li+ reference indicating a high probability of metallic lithium deposition. This significant downward shift is caused by higher interfacial resistance caused by a thicker SEI, which impedes Li+ transport and increases overpotential. It is vital to mention that while the SPM framework can predict anode potential becoming negative, an indicator of high probability of Li-plating, this degradation mechanism cannot be modeled effectively using the SPM framework due to the absence of electrolyte phase in the model. Consequently, although the model captures the SEI-driven resistance growth and capacity loss, it may underestimate the severity of degradation under high C-rate conditions as it neglects additional kinetic limitations and side reactions such as Li-plating.
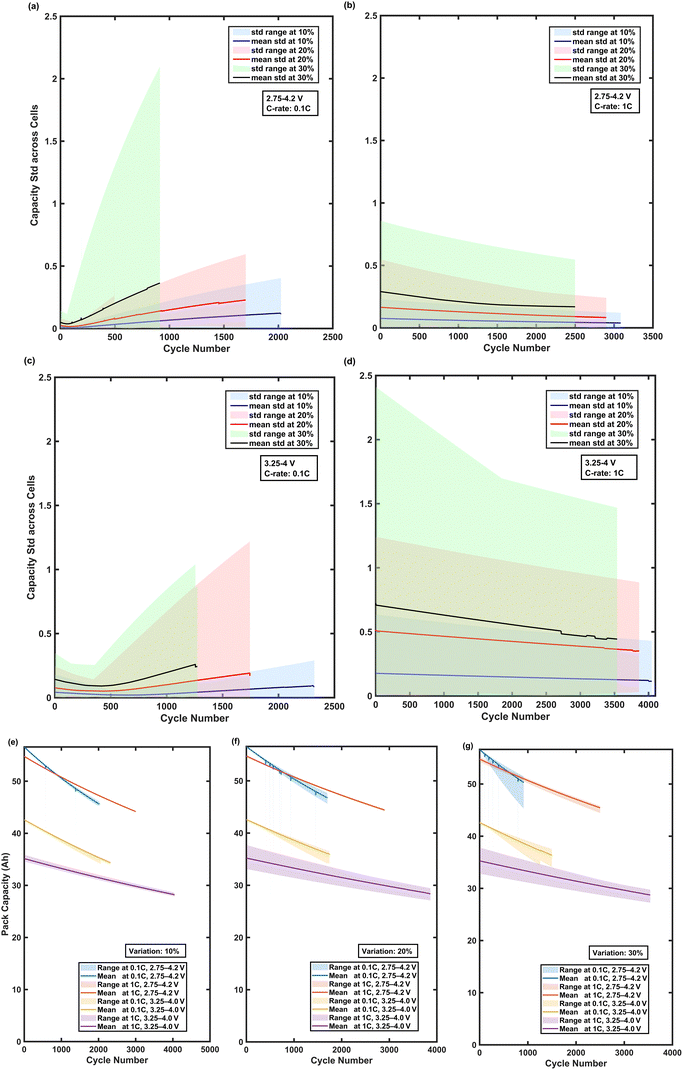
Fig. 4 shows the mean as well as the spread of the predicted outcomes from multiple simulation runs to provide a statistically meaningful assessment of how random particle radii variation affects the cells’ capacity and the overall battery pack degradation. To ensure this, the simulations were repeated until the standard error of the mean (SEM) across cells’ capacities dropped below a threshold of 5%. The plots in the first row, Fig. 4(a) and (b), show the evolution of the SD of capacity across cells over the cycle life. The solid line shows the SD averaged over all simulation runs, while the shaded region shows the statistical spread of the outcomes with greater than 5% probability (i.e., 95% confidence interval). At 0.1C, the capacity SD is strongly influenced by the variation in particle radii, with the 30% variation reaching a capacity SD of around 2.5 Ah by around 2000 cycles, in comparison to just 0.4 Ah at 10% variation, approximately. It should be noted that the capacity SD is similar across all % variation cases at BOL for 0.1C, but the gap between them widens with cycling. This can be attributed to the fact that the variation in the specific area available for electrochemical reactions across cells strongly influences SEI growth and thereby capacity loss. The other effects of variation in particle radii across cells, such as diffusion length and surface overpotential, are less relevant at low C-rate. However, at the higher C-rate of 1C, the capacity SD remains almost stable and moderate, even at 30% variation. It plateaued below 1.5 Ah by approximately 1000 cycles, highlighting that the higher C-rate helps keep cells behaving in a more homogenous manner and suppressing cell-to-cell divergence. In fact, the capacity SD is much higher at BOL compared to 0.1C case and drops slightly. This suggests that the effect of particle radii variation on diffusion and kinetics, and thereby usable capacity, is more important than its effect of SEI growth, which is responsible for the slight reduction in capacity SD with cycling. As previously mentioned, this is in the absence of Li-plating which may fundamentally change the trends shown here.
The set of plots in the second row, Fig. 4(c)–(e), shows the mean battery pack capacity and the spread in battery pack capacity over cycles for the three variation levels considered. Similar to the capacity SD plots, the solid line in these plots shows mean pack capacity across the many runs performed using randomly drawn particle radii from the respective normal distributions for each run. The shaded region about the solid line shows the statistical spread of the outcome with a probability of 5% or more. At 0.1C, the statistical spread in pack capacity becomes larger with cycling, especially in the 30% case, where the spread widens to about 8 Ah near the end of life. At 1C, however, even at 30% variation, the spread remains narrow (i.e., 3–5 Ah), and the mean pack capacity stays close to the overall trend across all runs, reinforcing that a high C-rate during the operation seems to mitigate the stochastic effects of manufacturing differences. It should be noted that the simulations performed in the study included the assumption that SEI growth is the dominant degradation mechanism and, hence, these findings may not hold true if a different degradation mechanism were to be dominant in a particular cell type/chemistry for the set of operating conditions being considered in this study.
All series electrical configuration—4S1P
The second case study involves a battery pack with a 4S1P electrical configuration cycled at two voltage windows, 2.75–4.2 V and 3.25–4 V, using the simulation methodology detailed previously. This case study is performed to understand how the variation in particle radius across cells operating at the same C-rate influences voltage divergence and how this ultimately affects the capacity fade trajectory at both the cell level and collectively as a pack.As reflected in the data, for the 10% variation case, cell 1 has the largest particle radius of 2.58 µm, while cells 2, 3, and 4 have smaller particle radii, 1.55 µm, 1.49 µm, and 1.46 µm, respectively. According to Table 1, under a broader voltage window of 2.75–4.2 V, the initial capacity of the battery pack 27.8 Ah, approximately, drops below 22.3 Ah after 2847 cycles. Under a narrower voltage window of 3.25–4 V, the cycle life extended to 3918 cycles, with the pack capacity dropping from around 17.9 Ah to below 14.4 Ah. For the 20% variation case, cell 2 has the largest particle radius of 3.12 µm, while cells 1, 3, and 4 have particle radii of 1.04 µm, 1.2 µm, and 0.997 µm, respectively, resulting in 2667 cycles under the broader voltage window and 3510 cycles under the narrower voltage window of 3.25–4.0 V. The most extreme heterogeneous behavior is observed for the 30% variation case, where cell 4 with the largest particle radius of 3.59 µm and cells 1 to 3 having smaller radii of 0.3 µm, 0.22 µm, 0.62 µm, leading to the shortest cycle life: 1319 cycles under a voltage window of 2.75–4.2 V and 1401 cycles under a voltage window of 3.25–4 V. Based on the pack capacity analysis, the narrower voltage window of 3.25–4 V extended the cycle life by 37.6%, 31.6%, and 6.2% for the 10%, 20%, and 30% variation cases, respectively.
Fig. S4 shows the SEI thickness for individual cells over their cycle life. Based on this figure, the cells with larger particle radii consistently maintain the thickest SEI layer, especially under a broader voltage window of 2.75–4.2 V. However, according to Fig. 5, the same cells experience the least capacity loss through SEI formation during their lifetime. For the 30% variation case, under a broader voltage window, cell 4 has the thickest SEI layer, as confirmed by Fig. S3 (i.e., approximately 143 nm after 1319 cycles), compared to cells 1 to 3 with SEI thickness ranging from 23 nm to 36 nm. However, Fig. 5 indicates that cell 4 experiences the least capacity loss of around 2.8 Ah after 1319 cycles, compared to the roughly 3.8 Ah to 6.2 Ah capacity loss in cells 1 to 3, despite their thinner SEI layers. This observation revealed that the thicker SEI layer in cells with larger particles are due to the lesser surface area available for the SEI to grow over. Total SEI growth in the cells with larger particle radii remains lower than in small-particle cells with larger specific surface areas. The same pattern can be observed at 10% and 20% variations. Regarding the narrower voltage window, the same pattern is observed; however, the voltage window of 3.25–4 V slows down SEI formation across all cells, thereby mitigating uneven aging and capacity loss. According to the observations, the overall capacity loss and the disparity in capacity loss across four cells under both voltage windows intensified as the particle radius variation increased from 10% to 30%.
Fig. 6 shows the voltage profiles at the BOL and EOL for the 10% and 30% variation cases under both voltage windows. At the BOL, under both broader and narrower voltage windows, the voltage profiles show only a small difference across cells at the lowest variation of 10%. In comparison, there is a considerable divergence across cells’ voltage profiles at the higher variability level of 30%. Under 2.75–4.2 V window for the 30% variation case, the cell with the largest particle radius, cell 4, discharged close to 2.1 V, which is significantly below the intended cell-level cut-off voltage of 2.75 V. During the charging phase, the same cell (i.e., cell 4, with the largest particle radius) displayed higher voltage plateaus, reaching up to 4.3 V at the end of constant-current mode (CC) vs. approximately 4.15 V for the other three cells with smaller particle radii. The same trend was observed at a 10% variation, albeit with a smaller disparity across cells. This trend reversed as the pack reached the end of its life. At EOL, for the 30% variation case, the cell with the largest particle radius (i.e., cell 4) only reach 3.3 V at the end of discharge, while the cells with a smaller particle radius over-discharged to around 2.1 V, becoming the most degraded member of the battery pack, thereby dictating the pack capacity. The narrower voltage window of 3.25–4 V minimized these effects, with the cell voltages not going below 3 V at the end of discharge for all cases, and at EOL, only for the 30% variation case, the cell with the thinnest SEI layer reached the end of discharge at around 2.95 V. In general, the narrower voltage window results in less voltage disparity among cells and increases the cycle life of the battery pack for all three levels of variations compared to the broader voltage window case. This occurs because battery operating over a broader voltage range results in the electrodes and electrolyte facing more extreme conditions. As a result, the electrolyte experiences greater degree of decomposition, which leads to greater amount of SEI formation. While SEI growth can be self-limiting, deep cycling in broad voltage ranges can cause repeated breakdown and regrowth. In contrast, narrower voltage windows reduce decomposition events, resulting in a lower rate of degradation.
 | ||
| Fig. 6 Cell voltage profiles at BOL and EOL for a 4S1P configuration under varying particle radii. Panels (a)–(d) correspond to 2.75–4.2 V, while panels (e)–(h) correspond to 3.25–4 V. | ||
It is worth mentioning the trend that is observed in the anode surface concentration to get a deeper understanding of intercalation dynamics. All cells indicate similar V-shaped concentration profiles at BOL, under both voltage windows. Regardless of the particle radius size and variability, all cells reach the lower limit of concentration at the end of discharge and recover close to the concentration upper limit at the end of the charging phase. However, at EOL, a significant disparity exists, especially in the 30% variation case. Under both voltage windows, the cells with a smaller particle radius exhibit a much lower surface concentration at the end of both the discharge and charging phases. This observation reveals that there is a substantial lithium depletion as well as a reduction in intercalation efficiency over cycling. However, the cells with the largest particle radius maintain higher surface concentration at all times. This observation confirms that their lower specific surface areas protect them from substantial depletion over cycles. Moreover, based on the anode potential plotted over time (Fig. S7) at BOL and EOL under 2.75–4.2 V window, the cells with the largest particle radius, regardless of the level of variations, experience a larger downward shift in the anode potential by the end of CC-charge mode compared to cells with smaller particle radii. This is an indicator of higher resistance due to their thicker SEI layer. The same pattern is observed under a narrower voltage window of 3.25–4 V. Hence, although cells with larger particles may experience less capacity loss due to overall less SEI formation, the thicker SEI formed in these cells may lead to greater resistance increase.
Fig. 7 indicates the capacity spread generated from multiple simulation runs to provide a statistically meaningful assessment for the 4S1P case, particularly in the context of how random particle radius variation affects the cumulative SEI capacity loss across cells and the overall battery pack degradation. Fig. 7(a) and (b) indicates the cumulative SEI-induced capacity loss SD over the cycle life of a battery pack. According to the plots, the SD increases with cycling, reflecting the compounding divergence in SEI formation across the cells with varied particle radii. As expected, the degree of spread becomes larger as the level of variation increases from 10% to 30%. For the 2.75–4.2 V case (Fig. 7a), the SD for the 30% variation case reaches almost 0.025 Ah after about 2200 cycles, while for the 10% variation case, it remains below 0.01 Ah even after 2800 cycles. Although the overall SEI loss is slightly lower, the same trend can be observed for the narrower voltage window of 3.25–4 V (Fig. 7b). These results suggest that the broader voltage window of 2.75–4.2 V accelerates cell degradation, thereby amplifying the effects of manufacturing differences. An increase in the SD would indicate that although the absolute capacity loss for each cell through SEI is small, the difference between the least degraded cells and the most degraded cells grows steadily over time, thereby reinforcing the risk of imbalance during long term operation.
Fig. 7(c)–(e) presents the evolution of 4S1P-configuration pack capacity for 10%, 20%, and 30% variations, respectively. Each plot shows capacity trends under both voltage windows. According to the plots, the mean pack capacity degrades faster under a broader voltage window of 2.75–4.2 V across all three cases. Another observation is that the statistical spread in a pack capacity increases with both cycle number and variation level. For the 30% case (Fig. 7e), the spread becomes significantly larger after around 2000 cycles, where the divergence between the top and bottom percentiles reaches 3 Ah. This divergence is particularly pronounced in the blue-shaded region (2.75–4.2 V), consistent with the stronger amplification of non-uniform degradation under more aggressive cycling conditions. The spread is more moderate under a narrower voltage window of 3.25–4.0 V, and the pack capacity spread converges over cycles, but still a non-negligible spread is observed, indicating that cell-to-cell variation has a long-term influence on pack performance regardless of the voltage window. It is important to note that the 4S1P configuration exacerbates the consequences of particle size variations across cells, since the weakest cell dictates the pack capacity. Therefore, even small differences in the physical properties of the cells might lead to significant uneven aging in the battery pack and increase its overall aging rate. These findings reinforce that in series-dominant architectures like 4S1P, the combination of broader voltage windows, high variation in the particle radius, and large number of cycles can increase the level of uneven aging. The use of a narrower voltage window or smaller manufacturing variation level in the cells’ particle radius can help suppress this divergence.
Series-parallel electrical configuration – 2S2P
The last case study involves a battery pack with a 2S2P electrical configuration cycled at two C-rates, 0.1C and 1C, and under both broader and narrower voltage windows of 2.75–4.2 V and 3.25–4 V, respectively. As per the simulation results, the higher particle radius variations (e.g., 30%) significantly shorten cycle life, particularly at a lower C-rate of 0.1C, where uneven aging is more pronounced. The cycle life consistently diminishes across all combinations of operating conditions as the particle radius variation escalates from 10% to 30%. The decline in cycle life is more significant at the lower C-rate of 0.1C, where uneven aging caused by SEI degradation mechanism becomes more severe. For instance, for the 30% variation case at 0.1C and broader voltage window, the cycle life significantly decreases to 815 cycles, compared to 2021 cycles for the 10% variation case (Table 1). Furthermore, cycling under a narrower voltage window alleviates the impact of uneven aging, resulting in a significant improvement in cycle life irrespective of the C-rate. However, the influence of the voltage window proved to be less effective as the particle radius variation increased. As mentioned earlier, the modeling framework used in this study only accounts for SEI growth as the degradation mechanism. Consequently, alternative or additional aging mechanisms, such as Li-plating and particle cracking, which are recognized to become prominent at elevated C-rates, are not present in this model. Hence, the model may underestimate aging at high C-rates. The conclusions derived are consequently restricted to SEI-driven aging trends, which appear to be more susceptible to uneven aging at lower C-rates.Cell capacity trends over time, as shown in Fig. 8 and 9, clearly demonstrate the impact of particle radius variation on uneven aging under different operating conditions. Across all conditions, cells with a smaller particle radius consistently exhibited greater capacity loss due to the larger specific surface area available for side reactions. The effect is particularly pronounced at the lower C-rate of 0.1C where capacity divergence between cells becomes more severe as cycling progresses. For the 30% variation case, cell 1 and cell 2, with particle radii of 3.49 µm and 3.77 µm, cycled at 0.1C under 2.75–4.2 V, faded from 28.1 Ah to 26.1 Ah, approximately. This is around 2 Ah capacity loss over cycles at a rate of approximately 2.48 mAh per cycle. Cell 3 and cell 4, with the smallest particle radii of 0.68 µm and 0.29 µm, faded from approximately 28.3 Ah to 19.9 Ah, an 8.44 Ah loss at rate of approximately 10.36 mAh per cycle. At 1C and under 3.25–4.0 V, cell 1 and cell 2 experienced capacity loss of around 1.2 mAh per cycle, while cell 3 and cell 4 experienced capacity loss of around 2.7 mAh per cycle. In contrast, one of the least severe cases occurs in the 10% variation case at 1C under the narrower voltage window, where cell 3 and cell 4 with the largest particle radii lost roughly 2.6 Ah at a rate close to 0.7 mAh per cycle, while cell 1 and cell 2 with the smallest particle radii lost approximately 3.7 Ah at a rate slightly over 0.9 mAh per cycle, which amounted to a 44.0% greater capacity loss for cell 1 and cell 2. At the 10% variation scenario, the capacity loss is significantly smaller compared to the 30% variation scenario, and the gap between the cells remained relatively limited. Furthermore, at a higher C-rate of 1C, regardless of the variation level, there was a significant difference in the initial capacity of the cells. However, over their lifetime, this difference diminished. In contrast, the opposite behavior was observed at a lower C-rate of 0.1C, where cells’ capacity diverged more as they cycled, confirmed by Fig. 8(a)–(c) and 9(a)–(c). At 1C, especially under a narrower voltage window of 3.25–4 V, the capacity of the cells with a larger particle radius is always considerably lower than the cells with a smaller particle radius as shown in Fig. 9(d)–(f). This is due to less available specific surface area for the intercalation of the lithium ions in the larger-particle cells.
Fig. S11 shows the SEI growth over time for all cases. For the 10% variation case, at 0.1C under 2.75–4.2 V window, cell 3's SEI layer grew to 178 nm, while cell 2 reached 136 nm, despite the higher capacity fade of cell 2. For the 20% variation case, at 0.1C under 2.75–4.2 V window, cell 1's SEI layer grew to 180 nm, while cell 3 reached 105 nm, yet cell 3 experienced 72.8% greater capacity loss. One reason behind this phenomenon is that the cells with a larger particle radius develop a thicker SEI layer but not more SEI growth, because the interface area over which SEI is spread is less than the cells with a smaller particle radius. In contrast, cells with smaller particle radii possess a much higher surface area, resulting in the SEI layer being thinner, yet the total volume of SEI is larger, consuming more lithium and leading to greater capacity loss. For the 30% variation case, at 0.1C under 2.75–4.2 V window, cell 1's SEI layer grew to 103 nm, while cell 3 reached 54.9 nm, with cell 3, according to Fig. 8, experiencing considerably greater capacity loss, reflecting its higher surface area's susceptibility to SEI formation over time. The same trend is observed under the other operating conditions for three different levels of variation. According to the observation, cells with larger particle radii show a thicker SEI layer all the time, but their thicker SEI layer is not large enough to make up for the lesser specific surface area compared to cells with smaller particle radii.
Voltage and scaled current profiles, as shown in Fig. 10 and 11, provide further insight into uneven aging. At the EOL, the voltage profiles across all levels of variation (i.e., 10% to 30%) reveal distinct patterns of divergence that were not seen at the BOL. While BOL indicates overlapping voltage profiles across the four cells, the EOL plots clearly indicate the effect of cell-to-cell variations on the voltage profiles of each individual cell by indicating the voltage separation, particularly under the 30% variation condition, as shown in Fig. 10(d) and 11(d). This separation indicates the progression of uneven aging, with some cells experiencing lower voltage cut-offs, revealing their higher internal resistance or lower remaining capacity. According to Fig. 10, at EOL for the 10% variation case, scaled current profiles during discharge indicate that cell 3 and cell 4, the cells with larger particle radii and belonging to the string with lesser degradation, deliver slightly more current than the nominal current (i.e., 1.1–1.2 × nominal current), while cell 1 and cell 2, the cells with smaller particle radii and belonging to the string with higher degradation, deliver lesser than the nominal current (i.e., 0.8–0.9 × nominal current). At 30% variations, the roles reverse, cell 1 and cell 2 deliver more current than the nominal current (i.e., 1.3–1.5 × nominal current), while cell 3 and cell 4 deliver lesser than the nominal current (i.e., 0.6–0.8 × nominal current). This behavior arises because both cells must carry the same current in a series string, and the overall string contribution to the pack current depends on the combined health of the two cells. A degraded string effectively becomes the “weak link”, unable to sustain the desired discharge current, forcing the healthier string to compensate by carrying a disproportionate share. At 1C, these effects become even more pronounced. The operation under higher current rate amplifies kinetic limitations, causing stronger current deviations between strings. For example, for the 30% variation case at 1C under a broader voltage window of 2.75–4.2 V, as shown in Fig. 10, the healthier string's current rose to about 1.7–2.0, while the degraded string's current dropped below 0.5 relative to the nominal current. Moreover, according to Fig. 8(f), cell 3 and cell 4, the two cells with a smaller particle radius, indicate higher initial capacities compared to cell 1 and cell 2 with a larger particle radius. The higher capacities arise from more available specific surface area, enhancing the intercalation kinetics, and lower diffusion limitation due to the shorter diffusion length. However, these cells degraded at a higher rate over their life due to higher loss of lithium inventory (LLI). The capacity curves of the smaller-particle cells intersect with the capacity curves of the larger-particle cells at approximately 1000 cycles, and after this intersection, the capacity of cell 3 and cell 4 continued to fade more steeply. Under the same operating conditions, such behavior is not observed at a lower variation case (i.e., 10% and 20%). Furthermore, cell 4 exhibits the thinnest SEI layer among all cells over the cycle life of the battery pack, while it has the highest rate of capacity fade. Further, cell 4 operates at a higher anode potential during the charging phase, as shown in Fig. S10, which suggests potentially lower rate of SEI formation. Despite of this, the dominant degradation mechanism in cell 4 appears to be LLI. This is likely caused by irreversible lithium consumption due to over-lithiation in the early cycles or imbalance-driven over-discharge during extended cycling, as confirmed by Fig. 10(d) which shows the voltage profile of all four cells at EOL.
Fig. 12(a)–(d) indicates the evolution of SD in the cells’ capacity in a battery pack with a 2S2P electrical configuration subjected to three different particle radius variations (i.e., 10%, 20%, 30%). Each scenario is simulated across multiple Monte Carlo runs until the SEM reached a threshold of 5%, ensuring a statistically reliable data set. At 0.1C and 2.75–4.2 V, as shown in Fig. 12(a), capacity SD indicates a growing divergence over their cycle life, with a more severity at a 30% particle radius variation. The capacity SD for a 10% and 20% particle radius variation remains below 0.6 Ah and 0.25 Ah by approximately 1500 and 2000 cycles, respectively; while by 1000 cycles, the capacity SD for the 30% variation is ∼2 Ah. This observation indicates that at low C-rates, even small deviations in microstructural properties like particle radius can considerably exacerbate uneven aging due to differences in the available specific surface area which leads to vastly different rates of SEI growth among cells. In contrast, at 1C and 2.75–4.2 V, as shown in Fig. 12(b), across all levels of variation, capacity SD remains low and decreases gradually. The highest SD belongs to a 30% variation case, and it remains under 0.6 Ah over the cycle life. The same behavior is observed under a narrower voltage window of 3.25–4.0 V, but with lower absolute capacity SD values. For instance, at 0.1C, as per Fig. 12(c), the 30% variation leads to a growing SD, reaching roughly 1 Ah by 1500 cycles, but it remains significantly lower than in the case of broader voltage window of 2.75–4.2 V (see Fig. 12(a)). This suggests that restricting the voltage window limits SEI-related degradation and delays divergence. Under 1C and 3.25–4.0 V operating condition, as shown in Fig. 12(d), capacity SD range indicates a higher deviation compared to the simulations under the same C-rate but a broader voltage window.
Fig. 12(e)–(g) indicate the evolution of pack capacity and its statistical spread across multiple simulation runs. At 10% variation, the pack capacity remains consistent across runs, with a marginal spread under all operating conditions. However, for 20% and 30% variations, the spread increases, notably at 0.1C under 2.75–4.2 V operating condition (e.g., in the 30% variation case, reached roughly 9 Ah after 1000 cycles). In contrast, operating at a higher C-rate of 1C consistently restricts the capacity spread, particularly when it is combined with a narrower voltage window of 3.25–4 V, where capacity degradation is minimized. This indicates that elevated C-rates and a narrower voltage window may mask the effects of manufacturing discrepancies, leading to a more uniform pack behavior despite the presence of variability in particle radius.
Scaling of uneven aging and parallel averaging effects
To evaluate how uneven aging scales with pack size, we computed the SD of per-cell percent capacity fade for five configurations, 2S2P (4 cells), 3S3P (9), 4S4P (16), 5S5P (25), 6S6P (36), 7S7P (49), and 9S9P (81), operated under identical conditions (0.1C, 2.75–4.20 V). Uneven aging was quantified as the per-cycle growth rate of the SD of per-cell capacity fade (%), which is estimated from the slope of SD with respect to cycle count. The resulting trend was non-monotonic: the 2S2P pack exhibited the lowest unevenness rate, the 3S3P and 4S4P packs showed higher unevenness rates, and the 5S5P, 7S7P and 9S9P packs exhibited decline in uneveness rates compared to 3S3P and 4S4P. This pattern is consistent with competing mechanisms: series connections accentuate weakest-cell bottlenecks (amplifying divergence), whereas parallel branches partially average cell-to-cell variability (damping divergence). Random placement of particles with larger/smaller radii among parallel branches further modulated the net effect, precluding simple proportional scaling with total cell count. Table 2 summarizes all discussed information.| Configuration | Cells | Uneven-aging rate (ΔSTD per cycle, %) | EOL (cycles to 80%) |
|---|---|---|---|
| 2S2P | 4 | 0.0104 | 1140 |
| 3S3P | 9 | 0.0213 | 326 |
| 4S4P | 16 | 0.0216 | 305 |
| 5S5P | 25 | 0.0170 | 298 |
| 6S6P | 36 | 0.0168 | 290 |
| 7S7P | 49 | 0.0165 | 281 |
| 9S9P | 81 | 0.0055 | 305 |
Pack end-of-life (EOL, 80% capacity) corroborated these observations to a certain extent as shown in Fig. 13. EOL dropped sharply when moving from 2S2P to 3S3P but then decreased more gradually with larger packs, indicating no statistically significant monotonic scaling of life with cell count. Collectively, these results suggest that increasing series count primarily governs the bottleneck behavior, while added parallelization provides partial mitigation via averaging. The combined evidence from the STD-growth metric and EOL analysis thus supports our interpretation that uneven aging does not scale linearly with pack size but rather reflects the balance between series-imposed constraints and parallel averaging.
 | ||
| Fig. 13 End-of-life (EOL) cycle number versus pack size for configurations ranging from 2S2P to 9S9P. The EOL was defined as the cycle number corresponding to 80% of the initial pack capacity. | ||
Conclusion
This study highlights the critical challenge of uneven aging in Li-ion battery packs, where variations in degradation rates among cells can lead to performance losses, safety risks, and reduced lifespan. While previous studies have focused on differences in cell resistance and capacity as contributors to this phenomenon, this work quantifies the effect of material-level variations, in particular mean active material particle size, on the cell- and pack-level aging characteristics. By incorporating SEI growth as a degradation mechanism in an electrochemical battery model, the study shows that even a small variation in the particle size can lead to considerable disparities in capacity fade among cells, ultimately affecting the pack's overall degradation trajectory. The results demonstrate that uneven aging is influenced not only by electrical configuration (i.e., series, parallel, and combined) but also by operating conditions such as C-rate and voltage window. Notably, lower C-rates and broader voltage windows exacerbate divergence in aging, while higher C-rates appear to suppress variation due to the effect of particle size on charge transfer kinetics. Further, this work also develops and implements a methodology to obtain statistically significant results to address the stochastic nature of manufacturing variations. As a result, this work shows reliable aging trends along with the statistical spread in the aging outcomes. The novelty of this work lies in tracing uneven pack-level aging back to microstructural origins, connecting cell- and pack-level aging behavior to the internal states of the battery, and providing insights into effective cell and pack manufacturing.Conflicts of interest
There are no conflicts to declare.Data availability
Supplementary information (SI) is available. The supplementary information contains additional simulation results, model validation, and supporting figures detailing anode potential evolution, SEI growth, surface concentration profiles, and statistical analyses for different pack configurations and operating conditions. See DOI: https://doi.org/10.1039/d5ya00182j.The codes will be made available on GitHub at kshah-ua/SPM-SEI-sim-code—multi-cell-system, and all the data, including raw data, will be shared via open science framework at https://osf.io/92szb/?view_only=c2743d5ea5c1423dae292dcafeffbe53.
References
- L. Gaines, K. Richa and J. Spangenberger, Key issues for Li-ion battery recycling, MRS Energy Sustainability, 2018, 5(13), 1–14, DOI:10.1557/mre.2018.13.
- M. A. Hannan, M. M. Hoque, A. Hussain, Y. Yusof and P. J. Ker, State-of-the-art and energy management system of lithium-ion batteries in electric vehicle applications: issues and recommendations, IEEE Access, 2018, 6, 19362–19378, DOI:10.1109/ACCESS.2018.2817655.
- T. Horiba, Lithium-ion battery systems, Proc. IEEE, 2014, 102(6), 939–950, DOI:10.1109/JPROC.2014.2313733.
- X. Liu, K. Li and X. Li, The electrochemical performance and applications of several popular lithium-ion batteries for electric vehicles – a review, Commun. Comput. Inf. Sci., 2018, 892, 19–34, DOI:10.1007/978-981-13-2381-2_19.
- T. Wulandari, D. Fawcett, S. B. Majumder and G. E. J. Poinern, Lithium-based batteries: history, current status, challenges, and future perspectives, Battery Energy, 2023, 2, 1–15, DOI:10.1002/bte2.20230030.
- D. Galatro, D. A. Romero, J. A. Freitez, C. Da Silva, O. Trescases and C. H. Amon, Modeling degradation of lithium-ion batteries considering cell-to-cell variations, J. Energy Storage, 2023, 62, 106011, DOI:10.1016/j.est.2023.106011.
- X. Feng, M. Ouyang, X. Liu, L. Lu, Y. Xia and X. He, Thermal runaway mechanism of lithium-ion battery for electric vehicles: a review, Energy Storage Mater., 2018, 10, 246–267, DOI:10.1016/j.ensm.2018.09.009.
- B. Klayman and W. Bernie, Tesla reports third fire involving Model S electric car, Reuters, 2013, available at: https://www.reuters.com/article/business/tesla-reports-third-fire-involving-model-s-electric-car-idUSBRE9A60U2.
- M. Baumann, L. Wildfeuer, S. Rohr and M. Lienkamp, Parameter variations within Li-ion battery packs – theoretical investigations and experimental quantification, J. Energy Storage, 2018, 18, 295–307, DOI:10.1016/j.est.2018.05.023.
- H. He and X. Chen, Analysing unbalanced ageing in EV battery packs using the low-cost lumped single particle model (LSPM): the impact of temperature gradients among parallel-connected cells, Transp. Res. Procedia, 2023, 70, 406–413 CrossRef.
- S. F. Schuster, M. J. Brand, P. Berg, M. Gleissenberger and A. Jossen, Lithium-ion cell-to-cell variation during battery electric vehicle operation, J. Power Sources, 2015, 297, 242–251 CrossRef CAS.
- Y. Lee, J. Park and W. Lu, A comprehensive experimental and modeling study on dissolution in Li-ion batteries, J. Electrochem. Soc., 2019, 166(7), A1193–A1202 Search PubMed.
- R. Gailani, R. Mokidm, M. Al-Greer, et al., Analysis of lithium-ion battery cells degradation based on different manufacturers, Proc. Int. Univ. Power Eng. Conf. (UPEC), 2020, pp. 1–6 DOI:10.1109/UPEC49904.2020.9209759.
- L. Wildfeuer, A. Karger and M. Lienkamp, et al., Experimental degradation study of a commercial lithium-ion battery, J. Power Sources, 2023, 543, 232498, DOI:10.1016/j.jpowsour.2022.232498.
- G. M. Trippetta, Y. Fang, A. Siddiqui, R. Lindstrom, G. Lindbergh and H. Ekström, Methods for characterization of heterogeneous aging in large lithium-ion batteries, ECS Meet. Abstr., 2023, 3411 CrossRef.
- G. Sordi, C. Rabissi and A. Casalegno, Understanding lithium-ion battery degradation through P2D model parameters evolution, ECS Meet. Abstr., 2023, 436 CrossRef.
- X. Zhang, S. Chumakov, X. Li, M. Klinsmann, S. U. Kim, C. R. Linder and J. Christensen, An electro-chemo-thermo-mechanical coupled three-dimensional computational framework for lithium-ion batteries, J. Electrochem. Soc., 2020, 167(16), 160542, DOI:10.1149/1945-7111/abd1f2.
- A. Allam and S. Onori, Exploring the dependence of cell aging dynamics on thermal gradient in battery modules: a PDE-based time scale separation approach, Proc. Eur. Control Conf. (ECC), 2019, pp. 1–6 Search PubMed.
- F. A. Lebel, P. Messier, A. Tessier and J. Trovão, Implications of lithium-ion cell variations on multi-cell battery pack thermal runaway, Proc. Veh. Power Propuls. Conf., 2019, pp. 5–12 Search PubMed.
- I. Zilberman, S. Ludwig and A. Jossen, Online aging determination in lithium-ion battery module with forced temperature gradient, J. Energy Storage, 2020, 27, 101170, DOI:10.1016/j.est.2019.101170.
- M. Loveridge, G. Remy and N. Kourra, et al., Looking deeper into the Galaxy (Note 7), Batteries, 2018, 4, 3 CrossRef.
- G. Zhao, X. Wang and M. Negnevitsky, Connecting battery technologies for electric vehicles from battery materials to management, iScience, 2022, 25(2), 103744 CrossRef CAS PubMed.
- M. S. Hosen, P. Yadav, J. Van Mierlo and M. Berecibar, A post-mortem study case of a dynamically aged commercial NMC cell, Energies, 2023, 16(4), 1046, DOI:10.3390/en16031046.
- Y. Olofsson, J. Groot, T. Katrašnik and G. Tavčar, Impedance spectroscopy characterization of automotive NMC/graphite Li-ion cells aged with realistic PHEV load profile: quantification of cell properties vs. temperature at different stages of ageing, Volvo GTT, Advanced Technology & Research, Göteborg, Sweden, and University of Ljubljana, Faculty of Mechanical Engineering, Ljubljana, Slovenia, 2023.
- I. Buchberger, S. Seidlmayer, A. Pokharel, M. Piana, J. Hattendorff, P. Kudejova, R. Gilles and H. A. Gasteiger, Aging analysis of graphite/LiNi1/3Mn1/3Co1/3O2 cells using XRD, PGAA, and AC impedance, J. Electrochem. Soc., 2015, 162(14), A2737–A2746, DOI:10.1149/2.0721514jes.
- M. Naylor Marlow, J. Chen and B. Wu, Degradation in parallel-connected lithium-ion battery packs under thermal gradients, Commun. Eng., 2024, 3(1), 2, DOI:10.1038/s44172-023-00153-5.
- M.-S. Wu, C.-Y. Lin, Y.-Y. Wang, C.-C. Wan and C. R. Yang, Numerical simulation for the discharge behaviors of batteries in series and/or parallel-connected battery pack, Electrochim. Acta, 2006, 52(3), 1349–1357, DOI:10.1016/j.electacta.2006.07.036.
- J. Brand, M. H. Hofmann, M. Steinhardt, S. F. Schuster and A. Jossen, Current distribution within parallel-connected battery cells, J. Power Sources, 2016, 334, 202–212 CrossRef.
- T. Bruen and J. Marco, Modelling and experimental evaluation of parallel connected lithium-ion cells for an electric vehicle battery system, J. Power Sources, 2016, 310, 91–101 CrossRef CAS.
- X. Liu, W. Ai, B. Wu and W. Ai, The effect of cell-to-cell variations and thermal gradients on the performance and degradation of lithium-ion battery packs, Appl. Energy, 2019, 251, 113381, DOI:10.1016/j.apenergy.2019.04.108.
- E. Hosseinzadeh, S. Arias, M. Krishna, D. Worwood, A. Barai, D. Widanalage and J. Marco, Quantifying cell-to-cell variations of a parallel battery module for different pack configurations, Appl. Energy, 2021, 282, 115859 CrossRef.
- W. Shi, X. Hu, C. Jin, J. Jiang, Y. Zhang and T. Yip, Effects of imbalanced currents on large-format LiFePO4/graphite batteries systems connected in parallel, J. Power Sources, 2016, 313, 198–204 CrossRef CAS.
- M. Fleckenstein, O. Bohlen, M. A. Roscher and B. Bäker, Current density and state of charge inhomogeneities in Li-ion battery cells with LiFePO4 as cathode material due to temperature gradients, J. Power Sources, 2011, 196(10), 4769–4778 Search PubMed.
- National Highway Traffic Safety Administration, Fire risk from quick-charging battery: Recall of 2021–2022 Nissan LEAF vehicles, U.S. Department of Transportation, 2 October 2025, https://static.nhtsa.gov/odi/rcl/2025/RCAK-25V655-7016.pdf.
- M. Woody, M. Arbabzadeh, G. M. Lewis, G. A. Keoleian and A. G. Stefanopoulou, Strategies to limit degradation and maximize Li-ion battery service lifetime – critical review and guidance for stakeholders, J. Energy Storage, 2020, 28, 101231 Search PubMed.
- R. Hausbrand, G. Cherkashinin, H. Ehrenberg, M. Gröting, K. Albe, C. Hess and W. Jaegermann, Fundamental degradation mechanisms of layered oxide Li-ion battery cathode materials: methodology, insights and novel approaches, Mater. Sci. Eng. B, 2014, 192, 3–25, DOI:10.1016/j.mseb.2014.11.014.
- C.-F. Chen, P. Barai and P. P. Mukherjee, An overview of degradation phenomena modeling in lithium-ion battery electrodes, Curr. Opin. Chem. Eng., 2016, 13, 82–90, DOI:10.1016/j.coche.2016.08.008.
- M. Börner, F. Horsthemke, F. Kollmer, S. Haseloff, A. Friesen, P. Niehoff, S. Nowak, M. Winter and F. M. Schappacher, Degradation effects on the surface of commercial LiNi0.5Co0.2Mn0.3O2 electrodes, J. Power Sources, 2016, 335, 45–55, DOI:10.1016/j.jpowsour.2016.09.074.
- M. M. Kabir and D. E. Demirocak, Degradation mechanisms in Li-ion batteries: a state-of-the-art review, Int. J. Energy Res., 2017, 41(15), 1963–1986, DOI:10.1002/er.3762.
- M. R. Palacín, Understanding ageing in Li-ion batteries: a chemical issue, Chem. Soc. Rev., 2018, 47, 4924, 10.1039/c7cs00889a.
- M. Jiang, D. L. Danilov, R.-A. Eichel and P. H. L. Notten, A review of degradation mechanisms and recent achievements for Ni-rich cathode-based Li-ion batteries, Adv. Energy Mater., 2018, 8(17), 1800233, DOI:10.1002/aenm.201800233.
- J. Miao, Review on electrode degradation at fast charging of Li-ion and Li metal batteries from a kinetic perspective, Electrochem, 2023, 3(1), 156–180, DOI:10.3390/electrochem3010013.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-ion battery materials: present and future, Mater. Today, 2015, 18(5), 252–264, DOI:10.1016/j.mattod.2014.10.040.
- G. Vennam, A. Sahoo and S. Ahmed, A survey on lithium-ion battery internal and external degradation modeling and state of health estimation, J. Energy Storage, 2022, 52, 104720, DOI:10.1016/j.est.2022.104720.
- H. Rauf, M. Khalid and N. Arshad, Machine learning in state of health and remaining useful life estimation: theoretical and technological development in battery degradation modelling, Renewable Sustainable Energy Rev., 2022, 156, 111903, DOI:10.1016/j.rser.2021.111903.
- J. Li, B. Liu, S. Li, D. Hu, L. Wang and J. Xu, Mechanistic modeling of Li plating in lithium-ion batteries, J. Power Sources, 2022, 521, 230936, DOI:10.1016/j.jpowsour.2022.230936.
- X.-G. Yang, Y. Leng, G. Zhang, S. Ge and C.-Y. Wang, Modeling of lithium plating induced aging of lithium-ion batteries: transition from linear to nonlinear aging, J. Power Sources, 2017, 360, 28–40, DOI:10.1016/j.jpowsour.2017.05.110.
- M. T. Lawder, P. W. C. Northrop and V. R. Subramanian, Model-based SEI layer growth and capacity fade analysis for EV and PHEV batteries and drive cycles, J. Electrochem. Soc., 2014, 161(14), A2099–A2108, DOI:10.1149/2.1161412jes.
- A. Weng, E. Olide, I. Kovalchuk, J. B. Siegel and A. Stefanopoulou, Modeling battery formation: boosted SEI growth, multi-species reactions, and irreversible expansion, J. Electrochem. Soc., 2023, 170(9), 090523, DOI:10.1149/1945-7111/aceffe.
- M. Safari, M. Morcrette, A. Teyssot and C. Delacourt, J. Electrochem. Soc., 2009, 156, A145–A153, DOI:10.1149/1.3043429.
- S. M. Jordan, C. O. Schreiber, M. Parhizi and K. Shah, A new multiphysics modeling framework to simulate coupled electrochemical-thermal-electrical phenomena in Li-ion battery packs, Appl. Energy, 2024, 360, 122746, DOI:10.1016/j.apenergy.2024.122746.
| This journal is © The Royal Society of Chemistry 2026 |