Open Access Article
Open Access ArticleOptimizing the Cu2+ ion and carbon-related defect center ratio in g-C3N4–ZnO:Cu nanocomposites for supercapacitor applications
Ana Varadiab,
Anca Silvestru c,
Adriana Popaa,
Dana Tolomana,
Arpad Mihai Rostas
c,
Adriana Popaa,
Dana Tolomana,
Arpad Mihai Rostas a,
Ameen Uddin Ammara,
Ion Nesterovschiad,
Maria Mihet
a,
Ameen Uddin Ammara,
Ion Nesterovschiad,
Maria Mihet a,
Sergiu Macaveia,
Lucian Barbu-Tudorana,
Cristian Leosteana and
Maria Stefan
a,
Sergiu Macaveia,
Lucian Barbu-Tudorana,
Cristian Leosteana and
Maria Stefan *a
*a
aNational Institute for Isotopic and Molecular Technologies, Donat 67-103, Cluj-Napoca, Romania. E-mail: maria.stefan@itim-cj.ro
bDoctoral School of Chemistry, Babeş-Bolyai University, Cluj-Napoca 400084, Romania
cSupramolecular Organic and Organometallic Chemistry Centre (CCSOOM), Chemistry Department, Faculty of Chemistry and Chemical Engineering, “Babeş-Bolyai” University, 400028 Cluj-Napoca, Romania
dDoctoral School of Physics, Babeş-Bolyai University, Cluj-Napoca 400084, Romania
First published on 18th December 2025
Abstract
In this work, we synthesised composite materials based on g-C3N4 as a carbon source, and ZnO doped with different Cu ion concentrations (ZnO:Cux, x = 0, 0.2, 0.4, 0.6, 0.8, and 1%) using multiple synthesis approaches. The synthesized g-C3N4–ZnO:Cu nanocomposites were characterised using advanced techniques like X-ray diffraction, scanning and transmission electron microscopy, Fourier transform infrared spectroscopy, and UV-vis adsorption and photoluminescence spectroscopy to evaluate the formation of the composite structure and the role of the dopant in the morpho-structural, optical, and compositional properties. Electron paramagnetic resonance spectroscopy and X-ray photoemission spectroscopy were employed to determine the carbon-related defect structure (VC) of the composite materials, which also revealed the presence of Cu ions in the ZnO lattice with a 2+ oxidation state. Electrochemical measurements, including galvanostatic charge–discharge and cycling stability tests, confirmed superior charge storage capacity, efficient electron transfer, and long-term durability. Notably, the g-C3N4–ZnO:Cu0.8-based supercapacitor device exhibited excellent cycling stability with 110% capacitance retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, along with the highest power (917.81 W kg−1) and energy density (25.24 Wh kg−1), making it a promising candidate for high-performance energy storage applications. The results indicate that an increase in the Cu concentration facilitates charge transport. The Cu-doped ZnO is primarily responsible for the pseudocapacitance mechanism in the supercapacitor device. Increasing the Cu doping concentration facilitates the appearance of redox reactions. However, once a certain dopant threshold is reached, any further increase in the dopant concentration results in a sudden drop in the current response, showing that the Cu2+/VC ratio plays an important role in the charge storage mechanism of the composites. Fine-tuning this ratio, which is a key parameter, has to be taken into account when designing carbon-based/metal oxide composite materials.
000 cycles, along with the highest power (917.81 W kg−1) and energy density (25.24 Wh kg−1), making it a promising candidate for high-performance energy storage applications. The results indicate that an increase in the Cu concentration facilitates charge transport. The Cu-doped ZnO is primarily responsible for the pseudocapacitance mechanism in the supercapacitor device. Increasing the Cu doping concentration facilitates the appearance of redox reactions. However, once a certain dopant threshold is reached, any further increase in the dopant concentration results in a sudden drop in the current response, showing that the Cu2+/VC ratio plays an important role in the charge storage mechanism of the composites. Fine-tuning this ratio, which is a key parameter, has to be taken into account when designing carbon-based/metal oxide composite materials.
1 Introduction
As the global economy grows and fossil fuels are depleted, the research and commercialization of sustainable renewable energy sources and related technologies have become critical worldwide.1,2 As a result, various energy-storage devices were invented.3 Classical energy storage systems such as capacitors and batteries continue to be used successfully. More recently, supercapacitors (SCs) have been gaining popularity due to their greatly enhanced features, including high specific capacitance, high power density, fast charge–discharge time, and long life cycle.4,5Supercapacitors are usually fabricated with electrode materials, electrolytes, and separators. Depending on the electrode materials, there are three main types of SCs: electric double-layer capacitors (EDLCs), pseudocapacitors, and hybrid supercapacitors.1,6 Each device stores energy through distinctive mechanisms,7–9 providing different outcomes dependent on the structure, composition, and stability of the applied electrode materials.8,10–14
EDLC SCs store the energy electrostatically, not by chemical reactions, and rely on forming an electric double layer at the interface between the solid electrode and the liquid electrolyte when a voltage is applied.7 The electrodes usually consist of high surface area carbon-based materials, such as activated carbon,10 g-C3N4,11 carbon nanotubes,10 graphene,12 graphene oxide,13 or reduced graphene oxide.12 It has the disadvantage of a low energy density, between 5 and 15 Wh kg−1, lower than those of other energy storage systems, such as Li-ion batteries (200–300 Wh kg−1), Li–air batteries (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 Wh kg−1), flow batteries (10–50 Wh kg−1) or fuel cells (800–10
140 Wh kg−1), flow batteries (10–50 Wh kg−1) or fuel cells (800–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Wh kg−1).14
000 Wh kg−1).14
Pseudocapacitors have attracted significant scientific interest due to their high specific capacitance and their potential integration into portable, automotive, and industrial energy systems. The development of pseudocapacitor electrodes has advanced from the early application of metal oxides RuO2, MnO2, and ZnO to the advancement of conducting polymers such as polyaniline and polypyrrole.15,16
Among the metal oxides used in SCs, zinc oxide is a critical, low-cost, and eco-friendly II–VI group semiconductor material with good electrochemical properties.17,18 Furthermore, during the ZnO synthesis, highly defective structures such as zinc vacancies (VZn), oxygen vacancies (VO), zinc interstitials (Zni), and oxygen interstitials (Oi) can be obtained, which should be investigated as they may enhance its electrochemical performance.19,20 Moreover, the concentration and type of defects within metal oxides can be effectively tailored by intentionally incorporating dopant species during doping, enabling precise control over the material's structural and electronic properties. Metals such as Cu,21 Mo,22 Fe,23 Li,24 or V22 used in doping processes can further enhance their supercapacitive behaviour.
Hybrid SCs combine an electric double-layer capacitor with a pseudocapacitor in a single device, thus combining the high energy density of batteries with the high power density and long cycle life of supercapacitors.9 Recently, carbon-based materials functionalized with metal oxides have been employed to enhance conductivity and surface area.15 When metal oxides are decorated with carbon-based materials, several structural, interfacial, and electronic defects can form, like oxygen vacancies, interfacial dislocations, charge transfer, and carbon lattice defects.25 Thus, defect engineering at the oxide–carbon interface is a key strategy for optimizing the performance of hybrid electrodes in supercapacitors.23,24,26
When combined with carbonaceous materials like GO, rGO, or g-C3N4, metal oxides provide an enhanced electron transfer path, high stability, excellent mechanical strength, and an increased specific surface area.27,28 The metal oxide contributes to pseudocapacitance through rapid and reversible redox reactions, while the carbon matrix stores charge via electric double-layer formation at the electrode–electrolyte interface. The intense interfacial contact between the two phases facilitates efficient charge transfer and ion diffusion, and the carbon's high surface area improves the utilization of redox-active sites. As a result, the hybrid electrode exhibits synergistic energy storage behavior, achieving both high energy density and excellent rate capability.29,30
Various metal oxides and carbon-based materials were examined as electrode materials for supercapacitor applications. Several studies reported that nanocomposites decorated with metal oxides such as SnO2,31 MnO2,32 Co3O4,33 and RuO2,34 and hybridized with rGO are quite interesting because they have tailor-made properties with enhanced performance compared to the individual materials.35
Wang et al.31 studied the supercapacitive performance of the as-prepared SnO2, rGO, and SnO2–graphene nanocomposite electrodes using the CV technique. The CV curves of SnO2, rGO, and SnO2–graphene nanocomposite electrodes were recorded at a scan rate of 10 mV s−1 within a potential window of 0–1 V. The SnO2–graphene nanocomposite electrode showed a specific capacitance of 347.3 F g−1, which is significantly higher than those of rGO (92.0 F g−1) and SnO2 (56.4 F g−1) under identical conditions, highlighting its superior capacitance and more efficient charge propagation within the electrode.
MnO2 decorated on carbon structures and used as an electrode material for supercapacitors exhibited remarkable improvements in electrochemical properties, as reported by Ramezani et al.32 The pure MnO2 achieved a specific capacitance of 55.7 F g−1, while MnO2–carbon nanotubes with 180 F g−1, and MnO2–graphene nanosheets with 310 F g−1 markedly surpassed it. Moreover, a ternary composite using a two carbon structure, a MnO2–graphene nanosheet–carbon nanotube composite, achieved a specific capacitance of 367 F g−1 at the same scan rate of 20 mV s−1, greater than all the previously reported values, emphasizing the synergistic integration of graphene nanosheets and carbon nanotubes, which collectively promote efficient electrolyte ion transport and reinforce the mechanical robustness of the electrode structure.32
In a study that compared the performances of ZnO and a g-C3N4–ZnO nanocomposite prepared using urea and thiourea precursors, as electrode materials, it was found that g-C3N4–ZnO with the urea precursor and the thiourea precursor exhibited higher specific capacitance values of 415 and 408 F g−1 compared to 223 F g−1 of pure ZnO with better cycling stability, indicating improved redox activity and superior charge storage ability.36
The present study focuses on advancements in supercapacitors through the development of hybrid electrode materials. Here, an innovative composite comprising g-C3N4 as a carbon source and copper-doped ZnO nanoflowers was synthesized and evaluated to demonstrate its supercapacitor performance. The nanocomposite has two distinct paramagnetic centers: the Cu2+ ions and carbon-related defect centers (VC). The spectral features associated with Cu2+ exhibit noticeable changes with increasing doping concentration, indicating a direct correlation between copper incorporation and the resulting magnetic environment, as evidenced by EPR spectroscopy. In contrast, the signal attributed to the C-related defect centers remains essentially constant, suggesting that these intrinsic defects are not significantly influenced by the level of Cu doping.37,38 The relative contribution of each paramagnetic species, expressed as the ratio of their EPR signals and normalized by linewidth and intensity, constitutes a key analytical parameter. This ratio provides valuable insight into the structural and electronic modifications induced by doping and is closely linked to the electrochemical behavior of the resulting material. Consequently, it serves as an important indicator for assessing and optimizing the nanocomposite's performance when employed as an active material in supercapacitor devices. Our study investigates supercapacitor challenges regarding material fabrication, cost, scalability, and limited energy storage.
2 Materials and methods
2.1 Chemicals
The reagents and solvents used in this research were of analytical grade and were used without any supplementary purification. The following reagents and solvents were used in the synthesis procedure: urea–CH4N2O (ACS Reag. Ph., VWR Chemicals) was used as a carbon source and a precursor for obtaining g-C3N4, sodium hydroxide–NaOH (Sigma Aldrich) was used as the precipitating agent in the ZnO synthesis, zinc nitrate hexahydrate Zn(NO3)2·6H2O (Alpha Aesar) was used as the zinc source, copper nitrate–Cu(NO3)2 (Alpha Aesar) was used to dope ZnO with Cu ions, sodium chloride–NaCl (ACS Reag. Ph., VWR Chemicals) was used to control the aggregation and distribution of the nanoparticles, and poly-allylamine hydrochloride–PAH (Alfa Aesar) was used as the linking polymer between ZnO:Cu and the carbon source. The aqueous solutions were prepared from Milli-Q water produced using a Direct-Q 3UV system (Millipore, Bedford, MA).2.2 Sample preparation
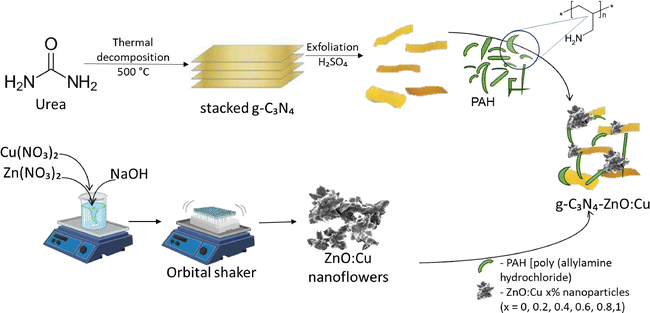
ZnO:Cu nanoparticles, having a nano-flower shape, were prepared through a chemical precipitation method as depicted in Scheme 1, where 10 mM of zinc nitrate hexahydrate was dissolved in 100 ml of distilled water under magnetic stirring, and NaOH 3 M was added until a pH of 12 was reached, followed by stirring on an orbital shaker for 4 h. The procedure is described in detail in a previous article by Stefan et al.39The amount of doping of Cu into ZnO is typically kept below 1% because the solubility of Cu2+ in the ZnO lattice is very limited. Higher concentrations lead to the segregation of secondary phases such as CuO, Cu2O, or metallic Cu, which distort the wurtzite structure, introduce significant lattice strain, and create defect states that act as non-radiative recombination centers. These effects degrade the optical, electrical, and catalytic performance of the material.40 At low concentrations (<1%), Cu can substitute Zn sites without severely perturbing the crystal lattice, enabling controlled modification of electronic states and enhanced visible-light absorption. However, excessive Cu doping increases Jahn–Teller distortions and defect formation, reduces carrier mobility, and shifts the material's behavior from intrinsic ZnO properties to those dominated by Cu-based phases.41,42 Thus, sub-percent Cu doping offers the best balance between structural stability and functional improvement.
g-C3N4 was obtained by the thermal decomposition of urea, heating it at 550 °C for 2 h as depicted in Scheme 2. The g-C3N4–ZnO:Cu nanocomposites were assembled from the two individual components using the linking polymer polyallylamine hydrochloride (PAH). The volumetric ratio between g-C3N4 and ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu was 1
Cu was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
A stock solution of 500 mL saline solution, 0.5 M NaCl, was prepared by weighing 14.6 g solid NaCl and adding water until 500 mL, with 2–3 minutes stirring until achieving complete dissolution. g-C3N4 was uniformly dispersed in the saline solution of PAH obtained by dissolving 0.7 g PAH in 100 mL NaCl 0.5 M by sonication for 4 h. The reaction mixture was heated to 80 °C for 18 h with continuous stirring, then cooled to room temperature. After centrifugation, the remaining material was added to an ethanol suspension of the ZnO:Cu nanoparticles and ultrasonicated for an additional 4 h. The mixture was centrifuged again, and the obtained precipitate was washed and dried at 65 °C. The entire synthesis procedure is summarized in Scheme 2.
2.3 Morpho-structural characterization methods
X-ray diffraction (XRD) measurements were performed on a Smart Lab Rigaku diffractometer with Cu-Kα radiation (λ = 1.54 Å). All measurements were conducted at room temperature over a 2θ range of 10–90°, with a 0.01° step. The nanocomposites' size, shape, clustering, and particle size distributions were examined with scanning transmission electron microscopy (STEM) on a Hitachi HD2700 electron microscope. Photoluminescence spectra (PL) were acquired on an FS5 spectrofluorometer (Edinburgh Instruments) equipped with a 150 W CW ozone-free Xenon arc lamp, a Czerny–Turner with a plane grating monochromator, and a PMT-900 emission detector. FTIR spectra were obtained in the 400–4000 cm−1 spectral range with a JASCO 6100 FTIR spectrometer using the KBr pellet technique. The spectral resolution to record the IR spectra was 2 cm−1. A JASCO V570 UV-VIS-NIR spectrophotometer equipped with an absolute reflectivity measurement accessory, JASCO ARN-475, was used to measure the absorption spectra. The UV-Vis absorption properties of the synthesized samples were investigated over the 200–800 nm spectral range. Raman measurements on all composites were performed using a Renishaw InVia Raman system paired with a Leica microscope. The excitation source was a near-infrared (NIR) diode laser at 830 nm. The Raman measurements covered a wavenumber range of 700–1650 cm−1 with a spectral resolution of 1 cm−1. Experiments used a 1 s laser exposure time and a single acquisition at 30 mW laser power. XPS qualitative and quantitative analysis of the composition of the samples was carried out with a custom-built SPECS spectrometer using a Mg anode (1253.64 eV) as the X-ray source. The samples were cast onto a sample holder. Spectra were analyzed with the CASA software using relative sensitivities, transmission factors, and electronic mean-free-path factors. Electron paramagnetic resonance (EPR) spectroscopy was performed at room temperature using a 9.88 GHz X-band Bruker E-500 ELEXSYS spectrometer. Nitrogen adsorption–desorption isotherms were recorded at 77 K using BelSorp MaxX equipment (Microtrac BEL Corporation, Japan). Sample pretreatment consisted of degassing under vacuum at 80 °C for 6 h before N2 sorption. The standard BET method was used to calculate the specific surface area (p/p0 in the range of 0.05–0.25), the total pore volume was estimated to be p/p0 = 0.95, and the pore size distribution was analyzed with the Barrett–Joyner–Halenda (BJH) method from the N2 desorption branch.2.4 Electrical property measurements
Symmetrical all-in-one supercapacitor devices were assembled using the g-C3N4–ZnO:Cu composite as an electrode material (3 mg) while using a 6 M KOH aqueous solution as an electrolyte (100 µL). A glass fiber separator was employed between the electrodes. A circular-shaped stainless-steel bolt on both sides of the device serves as a current collector. The areal mass loading of the electrodes on this device is approximately 2.65 mg cm−1, with a total mass of 3 mg per electrode. As the powder sample is directly loaded onto the current collector without a thin film or substrate, the focus is on measuring the performance of the synthesized sample; the electrode thickness is not measured. The focus remains on maintaining consistent mass loading across all devices. In the symmetric device, electrochemical testing was performed without any additional booster material, such as carbon, and only the mass of the single electrode was used to calculate specific capacitance and Ragone plot values to report the contribution from the individual electrode. A BioLogic VMP 300 electrochemical workstation was used to test the electrochemical performance of the assembled supercapacitor devices. The techniques included cyclic voltammetry (CV), potentiostatic electrochemical impedance spectroscopy (PEIS), and galvanostatic cycling with potential limitation (GCPL). CV measurements were performed within a voltage window of 0 to 1 V, with scan rates ranging from 2 to 200 mV s−1. PEIS was performed with an AC signal amplitude of 10 mV across a frequency range of 10 mHz to 1 MHz. GCPL tests were conducted at a current density of 0.8 A g−1, with the potential cycled over a 0–1 V window at a scan rate of 10 mV s−1. Specific capacitance, energy density, and power density were calculated based on the data from CV and GCPL as described in previous studies.24,393 Results and discussion
The general criteria for high electrochemical performance are chemical stability and surface features.43 These material-specific characteristics can be developed using appropriate synthesis procedures and by carefully optimizing the experimental parameters. Considering the variables above, g-C3N4–ZnO:Cux nanocomposites were prepared by combining previously synthesized individual components at the same volume ratio. The heterojunction was realized using poly(allylamine hydrochloride) (PAH) as a linking polymer. PAH is a cationic polymer with primary amine groups, making it highly water-soluble and reactive.44 Because of its strong electrostatic interactions, it is often used to synthesize composite materials.Thus, g-C3N4 was formed by thermal condensation followed by polymerisation of urea at around 550 °C. The obtained bulk g-C3N4 was ground into a fine powder, followed by chemical exfoliation with H2SO4 to obtain g-C3N4 nanosheets. The general chemical reactions for thermal decomposition of urea are described in the following order:45,46
 | (1) |
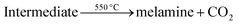 | (2) |
 | (3) |
In a separate synthesis procedure, copper-doped ZnO nanoflowers were obtained by chemical precipitating of zinc nitrate in sodium hydroxide as described in eqn (4) and (5).
| Zn(NO3)2 + 2NaOH → Zn(OH)2↓ + 2NaNO3 | (4) |
| Zn(OH)2 → ZnO + H2O | (5) |
The g-C3N4 nanosheets were functionalised with PAH to increase their reactivity. The newly existing functional groups contribute to forming new bonds in the g-C3N4–ZnO:Cu composites. Scheme 2 outlines the synthesis procedures for obtaining g-C3N4–ZnO:Cux nanocomposites.
The morphology of g-C3N4–ZnO:Cu was investigated by SEM and TEM microscopy, as shown in Fig. 1a–c. As an example, in Fig. 1a and b the images corresponding to pristine g-C3N4 and, respectively, ZnO nanoflowers are depicted, as well as a representative image of the composites, namely g-C3N4–ZnO:Cu0.4 (Fig. 1c). The TEM and SEM images in Fig. 1a show the presence of thin sheets, a morphology specific to g-C3N4. From the TEM and SEM images presented in Fig. 1b, the morphology of ZnO nanoparticles is revealed as elongated petal-like particles. The mean size of the ZnO:Cu particles is approximately 120 nm. In the case of the composite materials (Fig. 1c), it can be observed that several ZnO nanoparticles are firmly attached to the g-C3N4 thin sheets. It should be noted that comparable morphologies were obtained for all processed samples.
 | ||
| Fig. 1 SEM/TEM images of (a) g-C3N4, (b) ZnO nanoflowers, (c) g-C3N4–ZnO:Cu0.4 and (d) X-ray diffraction patterns of the g-C3N4–ZnO:Cu composites. | ||
The elemental analysis, as indicated by EDS mapping measurement results presented in Figure S-EDS (SI), reveals the presence of Zn, O, Cu, C, and N, confirming the assembly of ZnO:Cu nanoparticles attached to thin g-C3N4 sheets, and the presence of the Cu dopant ions distributed uniformly in the host ZnO lattice.
XRD was performed to identify the structural crystalline phases and the sample's structure. Fig. 1d shows the diffraction patterns of g-C3N4–ZnO:Cu composites. As observed, the diffractograms contain diffraction patterns specific to both composite material components. The peaks observed at 2θ = 12.71, and 27.47° are indexed to (100) and (002) corresponding to the planes of g-C3N4 (card JCPDS 79-0208), while all the other peaks correspond to the hexagonal wurtzite structure of ZnO (space group P63mc, JCPDS 79-0208). No other crystalline phases are present, showing the samples' purity. The cell parameters were calculated using Rietveld refinement and are summarized in Table 1. Cu doping causes a small increase in the cell volume up to 0.8 mol%, followed by a substantial drop at the higher Cu concentrations (1 mol%). Even though Cu2+ ions have an ionic radius (0.73 Å) similar to that of Zn2+ ions (0.74 Å), an increase in the unit cell volume is observed. This behavior can be explained by the fact that some Cu2+ ions partially replace Zn2+ ions, while others occupy interstitial sites. Interstitial positions can give rise to various lattice defects, such as Zn interstitials or oxygen vacancies. At a Cu doping concentration of 1 mol%, a significant reduction in the cell volume is observed, probably due to the segregation of Cu2+ ions on the surface of ZnO and the formation of zinc vacancies. The average crystallite size, calculated by the Williamson–Hall method, ranges from 11 to 14 nm.
| Sample | ZnO:Cu | g-C3N4 | SBET/m2 g−1 | Vp/cm3 g−1 | |||||
|---|---|---|---|---|---|---|---|---|---|
| a = b/Å | c/Å | V/Å3 | D/nm | a = b/Å | c/Å | V/Å3 | |||
| g-C3N4–ZnO:Cu0 | 3.243 | 5.199 | 47.37 | 12 | 6.492 | 2.516 | 91.8 | 16.15 | 0.043 |
| g-C3N4–ZnO:Cu0.2 | 3.243 | 5.202 | 47.39 | 11 | 6.492 | 2.516 | 91.8 | 16.19 | 0.042 |
| g-C3N4–ZnO:Cu0.4 | 3.246 | 5.196 | 47.39 | 12 | 6.492 | 2.516 | 91.8 | 19.84 | 0.056 |
| g-C3N4–ZnO:Cu0.6 | 3.247 | 5.196 | 47.40 | 14 | 6.492 | 2.516 | 91.8 | 19.02 | 0.051 |
| g-C3N4–ZnO:Cu0.8 | 3.243 | 5.199 | 47.36 | 10 | 6.492 | 2.516 | 91.8 | 21.80 | 0.063 |
| g-C3N4–ZnO:Cu1 | 3.241 | 5.195 | 47.26 | 13 | 6.492 | 2.516 | 91.8 | 20.61 | 0.057 |
FT-IR spectroscopy was used to investigate the functional groups and chemical bonds in the samples. Fig. 2a shows the FT-IR spectra of the g-C3N4–ZnO:Cu1 composite in the range of 350–2000 cm−1. At 412 cm−1, a broad and intense band corresponding to the stretching mode of the Zn–O bond is observed.47 The peak centered at 807 cm−1 is associated with the triazine units, while the peaks at 1235 cm−1 and 1637 cm−1 correspond to the C–N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching vibration modes of g-C3N4.48 The peak at 1315 cm−1 is assigned to C–C and C–N bending vibrations, whereas the band at 1402 cm−1 corresponds to the heptazine-derived repeating units.49 A shift to lower wavenumbers of the g-C3N4-specific peaks due to Cu doping of ZnO is observed (see Figure S-FT-IR (SI)). This shift indicates that the conjugated system of g-C3N4 was stretched, and a broadly conjugated system containing g-C3N4 and ZnO had formed.50
N stretching vibration modes of g-C3N4.48 The peak at 1315 cm−1 is assigned to C–C and C–N bending vibrations, whereas the band at 1402 cm−1 corresponds to the heptazine-derived repeating units.49 A shift to lower wavenumbers of the g-C3N4-specific peaks due to Cu doping of ZnO is observed (see Figure S-FT-IR (SI)). This shift indicates that the conjugated system of g-C3N4 was stretched, and a broadly conjugated system containing g-C3N4 and ZnO had formed.50
 | ||
| Fig. 2 (a) FT-IR spectra of the sample g-C3N4–ZnO:Cu1 and (b) estimation of the band gap energy Eg based on Tauc's equation for all the synthesized samples. | ||
UV-Vis spectroscopy was employed to investigate the optical properties of g-C3N4–ZnO:Cu samples, and the results are shown in Figure S-UV-Vis (SI). All samples exhibit significant absorption in the 200–400 nm range, consistent with the characteristic behavior of ZnO,51 with maximum absorption at 366 nm corresponding to interband transitions.39 Increasing the copper concentration shifts the absorption spectra towards higher wavelengths. The semiconductor's band gap energy (Eg) was calculated based on the absorption spectrum using Tauc's equation:52
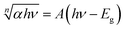 | (6) |
In this equation, α is the absorption coefficient, hν is the photon energy, A is a constant, and n is the Tauc exponent, which depends on the type of electronic transition (e.g., n = 2 for indirect allowed transitions and n = 1/2 for direct allowed transitions). To determine Eg, 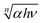 was plotted as a function of hν, and the linear portion of the graph is extrapolated to the x-axis to find the intercept corresponding to the band gap energy.
was plotted as a function of hν, and the linear portion of the graph is extrapolated to the x-axis to find the intercept corresponding to the band gap energy.
Fig. 2b shows the corresponding Tauc's plot with the band gap energy values for all samples, and a slight decrease is observed with increasing copper doping. The reduction in the band gap energy can be attributed to several factors: the presence of Cu d-states below the conduction band,53 the existence of a tensile stress induced by a mismatch between the dopant ions and Zn radius,54 the formation of defect levels due to doping within the band gap,55 and the strong sp-d exchange interaction between the band electrons of ZnO and the localized d electrons of Cu2+ ions substituting for Zn2+ ions, which shifts the Fermi level to the valence band.56 In the undoped state, the Fermi level is located at the center of the band gap, and its position depends on the type of semiconductor.39 Doping with Cu ions modifies the semiconductor's electrical and optical properties by introducing acceptor levels near the valence band. These levels facilitate electron excitation from the valence band, increasing the hole concentration and enhancing p-type conductivity. Copper has one fewer valence electron than zinc; that is why, when copper is introduced into zinc oxide, it acts as a p-type dopant and generates holes in the valence band.57 As the hole concentration increases, the Fermi level shifts downward, approaching the valence band. There are more unoccupied states (holes) at lower energies, and as a result, the Fermi level decreases.58 Cu doping often results in slightly reduced band gap energy due to the formation of localized states and increased electron–hole interactions. A similar behavior was reported by Ma et al.,58 who observed that increasing the Cu dopant concentration leads to a decrease in the optical band gap of Cu-doped ZnO.
The textural properties of the samples were evaluated using the BET method and are summarized in Table 1 and Figure S-BET (SI). As expected, we observe that both the specific surface area and the pore volume are almost unchanged with the Cu doping concentration. At a concentration of 0.8% Cu, a maximum of 21.8 m2 g−1 is obtained, after which a slight decrease is observed. In general, small variations in the specific surface area can arise from the synthesis procedure. The specific surface area is a key factor for materials used as electrode materials for supercapacitor applications, but as evidenced by the BET measurements, Cu doping of ZnO in the g-C3N4–ZnO:Cu composites does not influence the specific surface area, indicating that the improvements in specific capacitance, which are described in the following, are due to other factors.
The Raman spectra of the g-C3N4–ZnO:Cu samples have the characteristic vibrational signals of graphitic carbon nitride and show minor differences between all samples. As shown in Figure S-Raman (SI), several peaks are intense. The band at 706 cm−1 corresponds to the heptazine ring-breathing mode. The peaks at 751 and 767 cm−1 are attributed to out-of-plane deformations of the heptazine units, while the band at 977 cm−1 is assigned to an additional out-of-plane deformation of the heterocyclic rings. The vibrational modes at 1116 and 1152 cm−1 originate from C–N stretching and C–N–c in-plane bending. The 1232 cm−1 band is associated with C–N stretching. In the higher-frequency region, the bands at 1310 and 1350 cm−1 correspond to defect-related (D band) modes and C–N/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching, and the peaks at 1405 and 1481 cm−1 arise from C–N and C
N stretching, and the peaks at 1405 and 1481 cm−1 arise from C–N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching vibrations. The bands at 1558 and 1620 cm−1 fall within the graphite-like G-band region.59–61 To evaluate the defect concentration, the ratio of the intensity of the D region (1350 cm−1) to the G region (1558 cm−1) was calculated for each sample. A higher ID/IG ratio indicates a greater degree of structural disorder.62,63 The obtained values are as follows: undoped g-C3N4–ZnO-0.691, 0.2% Cu-0.642, 0.4% Cu-0.690, 0.6% Cu-0.697, 0.8% Cu-0.710, and 1% Cu-0.663. These results show that the 0.8% Cu-doped sample exhibits the highest ID/IG ratio, suggesting that this composition has the greatest defect concentration.
N stretching vibrations. The bands at 1558 and 1620 cm−1 fall within the graphite-like G-band region.59–61 To evaluate the defect concentration, the ratio of the intensity of the D region (1350 cm−1) to the G region (1558 cm−1) was calculated for each sample. A higher ID/IG ratio indicates a greater degree of structural disorder.62,63 The obtained values are as follows: undoped g-C3N4–ZnO-0.691, 0.2% Cu-0.642, 0.4% Cu-0.690, 0.6% Cu-0.697, 0.8% Cu-0.710, and 1% Cu-0.663. These results show that the 0.8% Cu-doped sample exhibits the highest ID/IG ratio, suggesting that this composition has the greatest defect concentration.
Further information on the material's structure, defects, and impurities was obtained through photoluminescence spectroscopy. The PL emission spectra were recorded at an excitation wavelength of 325 nm and are similar for all g-C3N4–ZnO:Cu samples, as depicted in Figure S-PL (SI). A broad emission band spanning 400–750 nm is observed. Because the broad response spanned a wide wavelength range, the spectra were deconvoluted with a Gaussian fit. This operation helps us identify the transitions responsible for the emissions and determine the positions of each spectral peak. The results are shown in Figure S-PLdeconv (SI) for g-C3N4–ZnO:Cu1 as an example. Also, the Gaussian peak fitting parameters (R2, residuals) are provided in Table S-PL (SI). According to previous PL studies, the bandgap states of g-C3N4 consist of an sp3 C–N σ band, an sp2 C–N π band, and the lone pair (LP) state of the bridging nitrogen atom. Thus, the emission band centered at 429 nm was assigned to the π* → π transition, the band at 451 nm to the σ* → LP transition, and the emission at 484 nm to the π* → LP transition.64 Compared to the emissions of g-C3N4, the composite samples show an enhancement of these emissions due to the charge recombination process at the interface of the two components.
XPS qualitative analysis was performed by examining the survey spectrum obtained from the g-C3N4–ZnO:Cu0.8 sample. In Figure S-XPS (SI), the expected Zn, O, C, and N elements are clearly observed. In addition, traces of Cl are present, originating from the synthesis reagents. The Cu 2p lines are not observed in the survey due to the low concentration; however, in the narrow-scan region, as shown in Fig. 3d, the data are quantifiable. Also, the expected Cu LMM Auger peak at BE = 334 eV is not marked because the more intense Zn LMM peak overlaps it.
XPS qualitative and quantitative analysis of the composition was carried out for the g-C3N4–ZnO:Cu0.8 sample, and the results are shown in Fig. 3a–d. The Zn 2p core-level doublet XPS spectra are shown in Fig. 3a. The doublets positioned at 1021.7 eV (2p3/2) and 1044.8 eV (2p1/2) are typical Zn2+ binding energy doublets. Also, two satellite peaks at higher binding energies were deconvoluted. The Cu 2p(3/2) core-level XPS spectrum is shown in Fig. 3b. There is a peak at 932.7 eV, while the calculated Cu/Zn ratio is 0.008, showing a good doping yield and the expected presence of Cu2+ ions, with no additional oxidation states. The C 1s core level line spectrum is presented in Fig. 3c. The deconvolution was performed by considering the specific lines of graphitic carbon nitride.65 The binding energy peaks are observed at 284.7 eV for C–C, 285.8 eV for C–O/C–N, and 287.5 eV for N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N. In this case, the C–C peak has a higher relative intensity, as expected for g-C3N4, due to the overlapping contribution from ZnO and g-C3N4 interactions.66 The N 1s core level line spectrum is presented in Fig. 3d. The deconvolution shows three peaks at 397.3, 398.3, and 400.0 eV, assigned to C–N
N. In this case, the C–C peak has a higher relative intensity, as expected for g-C3N4, due to the overlapping contribution from ZnO and g-C3N4 interactions.66 The N 1s core level line spectrum is presented in Fig. 3d. The deconvolution shows three peaks at 397.3, 398.3, and 400.0 eV, assigned to C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, N–(C)3, and C–N–H groups, respectively. The XPS analysis confirmed the successful Cu doping of ZnO and an interaction between ZnO with g-C3N4.
C, N–(C)3, and C–N–H groups, respectively. The XPS analysis confirmed the successful Cu doping of ZnO and an interaction between ZnO with g-C3N4.
The presence of Cu ions in the ZnO lattice and carbon-related defect centers in g-C3N4 was confirmed by EPR spectroscopy. The samples containing Cu show an axial EPR signal specific to Cu2+ ions in axial symmetry, with four parallel components centered at g‖ ≈ 2.36 having a hyperfine constant A‖ ≈ 150 G and one component at g⊥ ≈ 2.07 (see Fig. 3e). The hyperfine structure is due to the interaction between the electronic spin S = 1/2 of the Cu2+ ion and the nuclear spin I = 3/2 of the copper nuclei 63Cu and 65Cu.67,68 Additionally, at g = 2.01, the EPR spectra show a sharp line due to the unpaired electron localized in the π-conjugated structure of g-C3N4.69
The fact that g‖ > g⊥ > ge (where ge = 2.0023 is the g value for a free electron) suggests that the Cu2+ ions are subject to an elongated tetragonal distortion.70 Based on the Hamiltonian spin parameters, the covalent parameters for the in-plane σ bond can be evaluated using the following expression:71
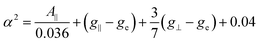 | (7) |
The obtained value for α2 is 0.84. It is known that for α2 = 1 the bond is fully ionic, and for α2 = 0.5 it is fully covalent. Considering the above results, it is not possible to clearly distinguish between covalent and ionic character. However, larger α2 values indicate that the in-plane σ bond is moderately ionic. As the concentration of Cu2+ ions increases, the EPR signal intensifies. The entire EPR spectra can be visualized in Fig. 3e.
To gain further insights into the importance of the paramagnetic ions, Cu2+ and C-related defect centers (VC), the EPR spectra were simulated using the Easyspin package.72 As depicted in Table 2, two spin systems were used for the simulations. The first system describes the Cu2+ centers, for which a spin 1/2 was employed with a hyperfine coupling. The broadening due to dipole–dipole interactions between the Cu2+ centers, or structural disorder due to the Cu-doping, was added to the system as so-called g- and A-strains, which are the line-broadening components of the g and A tensors. Dipole–dipole interactions are magnetic interactions between unpaired electron spins. In dilute solutions, this primarily leads to broadening of EPR spectral lines, with the line width proportional to the spin concentration, and even to splitting signals depending on their magnitude and orientation relative to the magnetic field. This interaction depends on the distance between the two spins and on the orientation of the vector connecting them with respect to the field vector.68 Structural disorder induced by Cu doping can broaden the EPR lines due to variations in the local atomic environment around the paramagnetic centers. Doping can introduce local distortions, alter crystal symmetry, and lead to the formation of defects or clusters, thereby creating a range of local magnetic fields and environments. This variation manifests as a broadened, asymmetric, or more complex EPR spectrum.73 The second system is associated with the VC defect centers, for which no changes in line position or width were observed. The weight parameter shows the direct ratio between the two signals (Cu2+/VC), being normalized with the line width and intensity of the two simulated signals. The Cu2+/VC ratio was plotted as a function of the Cu dopant concentration, and is depicted in Fig. 3f, where the simulation results are also shown in the inset. The ratio between the two paramagnetic centers increases rapidly until a 0.8% Cu concentration is observed after a slight saturation. These findings are further discussed in the electrochemical section of the manuscript, where they are related to the performance of the designed supercapacitor devices based on the g-C3N4–ZnO:Cu composites.
| Sample | Cu2+ | VC | Weight | ||||
|---|---|---|---|---|---|---|---|
| g‖ | g⊥ | A‖/MHz | gstrain | Astrain | gC | Cu2+/VC | |
| g-C3N4–ZnO:Cu0.2 | 2.355 | 2.0817 | 449 | 0 | 0 | 2.0109 | 1260 |
| g-C3N4–ZnO:Cu0.4 | 2.355 | 2.0817 | 449 | 0.07 | 80 | 2.0109 | 1343 |
| g-C3N4–ZnO:Cu0.6 | 2.355 | 2.0817 | 449 | 0.08 | 110 | 2.0109 | 1782 |
| g-C3N4–ZnO:Cu0.8 | 2.355 | 2.0817 | 449 | 0.095 | 140 | 2.0109 | 2081 |
| g-C3N4–ZnO:Cu1 | 2.355 | 2.0817 | 449 | 0.11 | 169 | 2.0109 | 2256 |
The electrochemical measurements of the prepared composites were conducted using them as electrode materials in a symmetric supercapacitor device, with 6 M KOH as an electrolyte and glass fiber as a separator. CV is a powerful technique for electrochemical analysis of supercapacitor devices, as it can provide valuable information on their reaction kinetics, electrical conductivity, and charge storage mechanism.
Fig. 4a shows the CV curves for all the tested supercapacitor devices measured at 100 mV s−1, while Figure S-CV (SI) shows the CV curves of the tested supercapacitors at different scan rates. In Fig. 4a, all supercapacitor devices display a similar quasi-rectangular shape, slightly deviating from the ideal electric double layer capacitance behavior. An ideal EDLC CV curve is a perfect rectangle, with the data following a constant–current, constant–voltage relationship.74 However, deviations from this ideal rectangular shape are associated with pseudocapacitance, as faradaic reactions at the electrode/electrolyte interface result in a sharp increase in current at the maximum voltage, as observed in all devices. The rounding of the edges of the perfect rectangle is due to the device's internal resistance, which is common in practical devices.75,76 The change in CV shape with increasing scan rate evident in all the devices as shown in Figure S-CV (SI) and for g-C3N4–ZnO:Cu0.8 in the inset of Fig. 4b shows that at lower scan rate ions have more time to penetrate pores and interact with redox-active sites and the CV curves shift more to an ideal EDLC shape.77,78
The CV shape suggests that charge storage in all devices is due to the combination of EDLC and pseudocapacitance mechanisms. This combination of charge storage mechanisms was expected, as the electrode material possesses EDLC-dominated contributions due to the g-C3N4 carbon-based material, and pseudocapacitance-dominated contributions due to ZnO:Cu.79 The lowest current response for g-C3N4–ZnO:Cu0 compared to those for other devices suggests the positive impact of Cu ions on the device's electrochemical performance. The trend of the CV results in Fig. 4a indicates that there is an increase in the current value with increasing Cu doping, with the g-C3N4–ZnO:Cu0.8-based supercapacitor device showing the highest current response, and the g-C3N4–ZnO:Cu1-based device showing a sudden drop in the current response.
The results indicate that an increase in the Cu concentration facilitates charge transport, as evidenced by EPR and XPS. The Cu-doped ZnO is primarily responsible for the pseudocapacitance mechanism in the supercapacitor device, as metal oxides can undergo fast, reversible redox reactions and ion intercalation.80 These results suggest that increased Cu doping increases the number of Cu2+ centers, as shown by EPR, thereby further facilitating the redox reaction. However, once a certain dopant threshold is reached, any further increase in the dopant concentration results in a sudden drop in the current response, which is also shown in Fig. 3f, which shows that the Cu2/VC ratio starts saturating as the concentration increases above 0.8%. The specific capacitance is a key performance parameter for supercapacitors, providing information on their energy and power density. The specific capacitance can be calculated from the CV curve at different scan rates using the following equation:
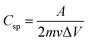 | (8) |
Fig. 4b shows the specific capacitance values of all the designed supercapacitor devices plotted as a function of scan rate, in line with the previous observations, and g-C3N4–ZnO:Cu0.8 shows the highest specific capacitance value at each scan rate closely followed by the g-C3N4–ZnO:Cu0.6-based supercapacitor device, but the graph shows that at lower scan rates 0.2, 0.4 and 0.6% Cu-based devices show almost identical specific capacitance values. The g-C3N4–ZnO:Cu0-based device shows the lowest specific capacitance value while the g-C3N4–ZnO:Cu1-based device the second lowest, which further validates our previous observation that although the Cu doping plays a critical role in improving the performance, after a certain doping percentage, an increase in the Cu content tends to limit the charge transport, probably due to structural degradation, which affects the surface area of the material and decreases the capacitance value by blocking potential electrochemical sites. As evidenced in Fig. 5, where the specific capacitance of the supercapacitor devices based on the composite materials is plotted as a function of Cu2+/VC ratio, the Cu2+/VC ratio is a key parameter that needs fine tuning to enhance the energy storage properties of the materials, playing a key role in the charge transfer and storage processes. An optimum doping concentration of around 0.8% Cu is observable.
 | ||
| Fig. 5 Specific capacitance values as a function of Cu2+/VC ratio, obtained from the simulated EPR spectra. | ||
To analyse the energy storage mechanism in the best-working composite, the contributions of diffusive and capacitive energy storage were assessed using the Dunn method.81 The equation used to calculate the contributions is expressed as
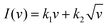 | (9) |
A Nyquist plot is a common representation of electrochemical impedance spectroscopy (EIS) data, where the imaginary impedance component is plotted as a function of the real component. Such plots provide information about electrode conductivity, electrolyte resistance, and double-layer capacitance. Fig. 6a presents the Nyquist plots of all tested supercapacitor devices. Each device exhibits an incomplete semicircle; the lowest-performing device, g-C3N4–ZnO:Cu1, displays the largest semicircle diameter, corresponding to the highest impedance. In contrast, the other devices show nearly similar semicircle diameters. However, the best-performing devices, g-C3N4–ZnO:Cu0.8 and g-C3N4–ZnO:Cu0.6, possess the lowest real impedance values.82,83
 | ||
| Fig. 6 (a) Nyquist plot, (b) galvanostatic charge–discharge measurements, and (c) capacitance retention as a function of the cycle number of the composite-based supercapacitor devices. | ||
To extract quantitative parameters from the Nyquist plots, equivalent circuit fitting (Z-fit) was performed. The fitted curves and the corresponding equivalent circuits are shown in Figure S-PEIS (SI). In the circuit, R1 (Rs) represents the solution resistance, corresponding to the intrinsic resistance between the electrode and electrolyte, while R2 (Rct) denotes the charge-transfer resistance. Q refers to a constant phase element (CPE), which accounts for deviations from ideal capacitor behavior. Specifically, Q1 corresponds to the double-layer capacitance (Cdl), and C2 or Q2 represents the pseudocapacitance, as discussed in the CV section. The element W corresponds to Warburg impedance, arising from ion diffusion processes in the electrolyte at low frequencies.84 The extracted parameter values from the equivalent circuit fitting are summarized in Table 3. Low Rs and Rct values, along with a high Cdl value for the g-C3N4–ZnO:Cu0.8-based SC design, highlight the superior performance of this device.
| Sample | Rs/Ω | Rct/Ω | Cdl/µF | W2/Ω s−1 | Csp/F g−1 | ED/Wh kg−1 | PD/W kg−1 |
|---|---|---|---|---|---|---|---|
| g-C3N4–ZnO:Cu0 | 4.587 (3.2%) | 190 (4%) | 20.4 (3.6%) | 513 (5%) | 23.21 | 3.22 | 118 |
| g-C3N4–ZnO:Cu0.2 | 0.345 (4.3%) | 115 (3%) | 40.00 (4%) | 243 (4.2%) | 151.4 | 21.02 | 764.00 |
| g-C3N4–ZnO:Cu0.4 | 0.2721 (3.2%) | 695 (2.8%) | 45.14 (6%) | 236 (4.6%) | 148.6 | 20.63 | 750.18 |
| g-C3N4–ZnO:Cu0.6 | 0.255 (7.2%) | 885 (6.3%) | 155.00 (2.2%) | 207 (3.7%) | 144.25 | 20.03 | 739.63 |
| g-C3N4–ZnO:Cu0.8 | 0.2989 (1.8%) | 177 (4.6%) | 204.00 (3.3%) | 167 (4.2%) | 181.83 | 25.24 | 917.81 |
| g-C3N4–ZnO:Cu1 | 0.778 (2.4%) | 367 (4.7%) | 30.13 (3.6%) | 396 (3.7%) | 91.99 | 12.77 | 464.36 |
Fig. 6b presents the galvanostatic charge–discharge measurements of the composite-based supercapacitor devices, carried out at a current density of 0.8 A g−1 within a voltage window of 0–1 V. The charge–discharge curves reveal the pseudocapacitance contribution, consistent with the CV and Dunn analysis results. In an ideal EDLC-type device, the GCD profile exhibits a perfectly triangular shape with complete symmetry between the charge and discharge curves.85,86 However, the presence of pseudocapacitance distorts this ideal shape.85 As shown in Fig. 6b, a plateau region appears at the maximum charging voltage, indicating the occurrence of faradaic processes.85 The g-C3N4–ZnO:Cu0.8 and g-C3N4–ZnO:Cu0.6-based SC devices, which also delivered the highest specific capacitance values, exhibit the longest discharge times. In contrast, the g-C3N4–ZnO:Cu1-based device, with the lowest specific capacitance, shows the shortest discharge time, demonstrating consistency across different measurements. S-GCD shows the charge–discharge curves measured at various current densities to analyze device performance further. The graphs follow a similar trend of the discharge time as observed in Fig. 6b, indicating that with the increasing current density, the device's performance remains stable. Fig. 6c illustrates the cycling stability of all devices, evaluated over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge–discharge cycles by plotting the capacitance retention as a function of cycle number. The results indicate good cycling stability across all devices, with the g-C3N4–ZnO:Cu0.6 device showing the lowest retention, maintaining nearly 80% of its initial capacitance after 10
000 charge–discharge cycles by plotting the capacitance retention as a function of cycle number. The results indicate good cycling stability across all devices, with the g-C3N4–ZnO:Cu0.6 device showing the lowest retention, maintaining nearly 80% of its initial capacitance after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. In contrast, the g-C3N4–ZnO:Cu0.8–C3N4–ZnO:Cu1 and based supercapacitor demonstrates outstanding stability, with capacitance retention gradually increasing during cycling and reaching almost 110% after 10
000 cycles. In contrast, the g-C3N4–ZnO:Cu0.8–C3N4–ZnO:Cu1 and based supercapacitor demonstrates outstanding stability, with capacitance retention gradually increasing during cycling and reaching almost 110% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. This enhancement in retention can be attributed to the progressive activation of electrode materials, improved electrode wettability, and/or structural modifications that provide more accessible active sites for ion storage. Figure S-Ret (SI) shows the first and last five charge–discharge cycles for C3N4–ZnO:Cu0.8 and C3N4–ZnO:Cu1 based devices, which showed retention higher than 100% to ensure that the charge phenomenon is intact and there is no noise or artifact in the signal.
000 cycles. This enhancement in retention can be attributed to the progressive activation of electrode materials, improved electrode wettability, and/or structural modifications that provide more accessible active sites for ion storage. Figure S-Ret (SI) shows the first and last five charge–discharge cycles for C3N4–ZnO:Cu0.8 and C3N4–ZnO:Cu1 based devices, which showed retention higher than 100% to ensure that the charge phenomenon is intact and there is no noise or artifact in the signal.
Table 3 shows the energy and power density values for all the supercapacitor devices tested in this study, derived from the highest specific capacitance value. The energy and power density were calculated using the following equations:
 | (10) |
 | (11) |
| Material | Cps/F g−1 | ED/Wh kg−1 | PD/W kg−1 | Ref. |
|---|---|---|---|---|
| ZnO | 86.4 | 1.8 | 2.9 | 87 |
| ZnO:Cu1% | 86.6 | 48 | 75 | 88 |
| g-C3N4–ZnO | 408 | — | — | 36 |
| g-C3N4-CuO | 98 | 14.8 | — | 89 |
| g-C3N4/TiO2/PP | 1216 | 65.6 | 249.9 | 90 |
| g-C3N4/NiO | 127 | 11 | 600 | 91 |
| g-C3N4/ZnO | 311 | 97.43 | 750 | 92 |
| g-C3N4/Fe2O3:Cu | 244 | 5.31 | 1000 | 93 |
| g-C3N4 | 78 | 19.33 | 500 | 94 |
| g-C3N4–ZnO:Cu0.8 | 181.83 | 25.24 | 917.81 | t.w. |
In this regard, Table 4 provides a general overview of the performance of these electrode materials, which helps contextualize the performance of our tested device. The best-performing electrode in our study, g-C3N4–ZnO:Cu0.8, exhibited a significantly higher specific capacitance than pristine g-C3N4 and Cu-doped ZnO electrodes reported in the literature, underscoring the promising electrochemical properties of the g-C3N4–ZnO:Cu composite. Furthermore, several studies listed in Table 4 reported g-C3N4–metal oxide composites with capacitance values comparable to or lower than ours; in contrast, our device demonstrates competitive or superior specific capacitance, energy density, and power density. These results highlight the excellent intrinsic electrochemical performance and strong potential of g-C3N4–ZnO:Cu composites as advanced electrode materials for supercapacitors.
4 Conclusions
The g-C3N4–ZnO:Cu nanocomposites were systematically investigated as electrode materials for supercapacitors. The nanocomposite samples were synthesized in several stages: in the first stage, separate components were formed, particularly g-C3N4 via thermal decomposition of urea and Cu-doped ZnO nanoflowers via chemical precipitation. These components were connected using polyallylamine hydrochloride. SEM and TEM investigations revealed uniformly distributed ZnO:Cu nanoflowers embedded within g-C3N4 layers. The incorporation and oxidation state of copper were confirmed using XPS and EPR spectroscopy. Doping introduces several lattice defects in the ZnO lattice, either via substitution or interstitial incorporation, thereby affecting its structural and optical properties. Thus, the developed composite samples have a crystalline structure with particle sizes ranging from 11 to 14 nm, and the band gap value decreasing from 3.15 to 3.08 eV. Electrochemical analysis confirmed that the charge storage mechanism originates from a synergistic contribution of EDLC and pseudocapacitance, with Cu doping enhancing conductivity and active site availability. The g-C3N4–ZnO:Cu0.8-based supercapacitor device exhibited the best overall performance, showing the highest specific capacitance (181.8 F g−1), energy density (25.24 Wh kg−1), and power density (917.81 W kg−1). At the same time, it demonstrated excellent long-term stability, with 110% capacitance retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. The importance of the ratio of carbon-based defect centers in the carbonaceous material g-C3N4 to the concentration of Cu2+ ions in ZnO was demonstrated, underscoring the crucial role of defect engineering in the design of supercapacitor electrode materials. These results highlight the potential of Cu-doped ZnO when used in composite materials with carbon-based materials, such as g-C3N4, making them promising candidates for next-generation energy storage devices.
000 cycles. The importance of the ratio of carbon-based defect centers in the carbonaceous material g-C3N4 to the concentration of Cu2+ ions in ZnO was demonstrated, underscoring the crucial role of defect engineering in the design of supercapacitor electrode materials. These results highlight the potential of Cu-doped ZnO when used in composite materials with carbon-based materials, such as g-C3N4, making them promising candidates for next-generation energy storage devices.
Author contributions
Ana Varadi: formal analysis, investigation, writing – original draft, writing – review & editing; Anca Silvestru: formal analysis, investigation, writing – review & editing; Adriana Popa: formal analysis, investigation, writing – original draft, writing – review & editing; Dana Toloman: formal analysis, investigation, writing – original draft, writing – review & editing; Arpad Mihai Rostas: formal analysis, writing – original draft, writing – review & editing, visualization; Ameen Uddin Ammar: formal analysis, writing – original draft, writing – review & editing; Ion Nesterovschi: investigation, writing – review & editing; Maria Mihet: investigation, writing – review & editing; Cristian Leostean: formal analysis, investigation, writing – review & editing; Sergiu Macavei: formal analysis, investigation, writing – review & editing; Lucian Barbu-Tudoran: formal analysis, investigation, writing – review & editing; Maria Stefan: conceptualization, validation, formal analysis, investigation, writing – original draft, writing – review & editing, visualization, supervision.Conflicts of interest
There are no conflicts to declare.Data availability
All information supporting the findings of this study are fully included within the main article and its accompanying supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5tc03960f.No additional datasets were generated or analyzed beyond those provided.
Acknowledgements
The authors would like to express appreciation for the financial support from the Ministry of Research, Innovation and Digitalization, Romania's National Recovery and Resilience Plan, PNRR-III-C9-2022-I8, CF 163/15.11.22, financing contract no. 760097/23.05.23.Notes and references
- N. I. Jalal, R. I. Ibrahim and M. K. Oudah, J. Phys.:Conf. Ser., 2021, 012015 CrossRef CAS.
- V. Joshi, V. Bachhar, S. S. Mishra, R. K. Shukla and M. Duseja, J. Mol. Struct., 2025, 143550 CrossRef CAS.
- C. Yang, D. Zhang, D. Wang, H. Luan, X. Chen and W. Yan, ACS Appl. Mater. Interfaces, 2023, 15, 5811–5821 CrossRef CAS.
- A. Berrueta, A. Ursua, I. San Martin, A. Eftekhari and P. Sanchis, IEEE Access, 2019, 7, 50869–50896 Search PubMed.
- J. Guo, D. Zhang, T. Li, J. Zhang and L. Yu, J. Colloid Interface Sci., 2022, 606, 261–271 CrossRef CAS PubMed.
- H. Aslam, A. Umar, M. U. Khan, T. Trivedi, G. Ezhilarasan, D. Bhanot, N. Abbas and K. F. Fawy, Rev. Inorg. Chem., 2025, 7 Search PubMed.
- W. Yang, M. Ni, X. Ren, Y. Tian, N. Li, Y. Su and X. Zhang, Curr. Opin. Colloid Interface Sci., 2015, 20, 416–428 CrossRef CAS.
- M. Saranya, R. Ramachandran and F. Wang, J. Sci.:Adv. Mater. Devices, 2016, 1, 454–460 Search PubMed.
- D. P. Chatterjee and A. K. Nandi, J. Mater. Chem. A, 2021, 9, 15880–15918 RSC.
- V. V. Obreja, Phys. E, 2008, 40, 2596–2605 CrossRef CAS.
- T. Jasna, S. K. Subrahmanian, V. Kavya, A. Haritha, T. Karthika, M. Shemeena, P. Jabira and B. N. Narayanan, J. Phys. D: Appl. Phys., 2024, 58, 035504 Search PubMed.
- T. Tene, S. Bellucci, M. Guevara, P. Romero, A. Guapi, L. Gahramanli, S. Straface, L. S. Caputi and C. Vacacela Gomez, Batteries, 2024, 10, 256 CrossRef CAS.
- B. Zhao, P. Liu, Y. Jiang, D. Pan, H. Tao, J. Song, T. Fang and W. Xu, J. Power Sources, 2012, 198, 423–427 CrossRef CAS.
- Y. Wang, K. Xue, X. Zhang, X. Zhang, P. Ma, B. Yang, S. Xu and J. Lang, Electrochim. Acta, 2023, 441, 141829 Search PubMed.
- I. Shaheen, I. Hussain, T. Zahra, M. S. Javed, S. S. A. Shah, K. Khan, M. B. Hanif, M. A. Assiri, Z. Said and W. U. Arifeen, et al., J. Energy Storage, 2023, 72, 108719 CrossRef.
- H. Zhang, D. Zhang, R. Mao, L. Zhou, C. Yang, Y. Wu, Y. Liu and Y. Ji, Nano Energy, 2024, 127, 109753 Search PubMed.
- J. Miao and B. Liu, Semiconductor Nanowires, Elsevier, 2015, pp. 3–28 Search PubMed.
- F. Pogacean, M. S tefan, D. Toloman, A. Popa, C. Leostean, A. Turza, M. Coros, O. Pana and S. Pruneanu, Nanomaterials, 2020, 10, 1473 Search PubMed.
- I. Ayoub, V. Kumar, R. Abolhassani, R. Sehgal, V. Sharma, R. Sehgal, H. C. Swart and Y. K. Mishra, Nanotechnol. Rev., 2022, 11, 575–619 Search PubMed.
- D. Toloman, A. Gungor, A. Popa, M. Stefan, S. Macavei, L. Barbu-Tudoran, A. Varadi, I. D. Yildirim, R. Suciu and I. Nesterovschi, et al., Ceram. Int., 2025, 51, 353–365 CrossRef CAS.
- S. Sivakumar, Y. Robinson and N. A. Mala, Appl. Surf. Sci. Adv., 2022, 12, 100344 Search PubMed.
- M. R. Pallavolu, J. Nallapureddy, R. R. Nallapureddy, G. Neelima, A. K. Yedluri, T. K. Mandal, B. Pejjai and S. W. Joo, J. Alloys Compd., 2021, 886, 161234 Search PubMed.
- S. Kumar, F. Ahmed, N. M. Shaalan, N. Arshi, S. Dalela and K. H. Chae, Nanomaterials, 2023, 13, 2222 CrossRef CAS PubMed.
- A. U. Ammar, M. H. Aleinawi, M. Stefan, A. Gungor, A. Popa, D. Toloman, K. Maškarić, E. Saritas, L. Barbu-Tudoran and S. Macavei, et al., Electrochim. Acta, 2025, 519, 145806 CrossRef CAS.
- M. Stefan, D. Toloman, A. Popa, A. Mesaros, O. Vasile, C. Leostean and O. Pana, J. Nanopart. Res., 2016, 18, 59 Search PubMed.
- M. Zhi, C. Xiang, J. Li, M. Li and N. Wu, Nanoscale, 2013, 5, 72–88 Search PubMed.
- S. Tamang, S. Rai, R. Bhujel, N. K. Bhattacharyya, B. P. Swain and J. Biswas, J. Alloys Compd., 2023, 947, 169588 CrossRef CAS.
- D. Zhang, C. Jiang and X. Zhou, Talanta, 2018, 182, 324–332 CrossRef CAS.
- G. Yu, X. Xie, L. Pan, Z. Bao and Y. Cui, Nano Energy, 2013, 2, 213–234 Search PubMed.
- H. Zhang, D.-Z. Zhang, D.-Y. Wang, Z.-Y. Xu, Y. Yang and B. Zhang, Rare Met., 2022, 41, 3117–3128 Search PubMed.
- Y. Wang, Y. Liu and J. Zhang, J. Nanopart. Res., 2015, 17, 1–10 CrossRef.
- M. Ramezani, M. Fathi and F. Mahboubi, Electrochim. Acta, 2015, 174, 345–355 Search PubMed.
- C. Xiang, M. Li, M. Zhi, A. Manivannan and N. Wu, J. Power Sources, 2013, 226, 65–70 CrossRef CAS.
- Z. J. Han, S. Pineda, A. T. Murdock, D. H. Seo, K. K. Ostrikov and A. Bendavid, J. Mater. Chem. A, 2017, 5, 17293–17301 RSC.
- B. Wang, D. Guan, Z. Gao, J. Wang, Z. Li, W. Yang and L. Liu, Mater. Chem. Phys., 2013, 141, 1–8 CrossRef CAS.
- S. Savarimuthu, M. Selvaraj and H. Chuang, Inorg. Chem. Commun., 2025, 178, 114555 CrossRef CAS.
- M. Sayed, B. Zhu, P. Kuang, X. Liu, B. Cheng, A. A. A. Ghamdi, S. Wageh, L. Zhang and J. Yu, Adv. Sustainable Syst., 2022, 6, 2100264 Search PubMed.
- D. Dvoranová, M. Mazúr, I. Papailias, T. Giannakopoulou, C. Trapalis and V. Brezová, Catalysts, 2018, 8, 47 Search PubMed.
- M. Stefan, A. M. Rostas, A. U. Ammar, A. Gungor, E. Saritas, D. Toloman, A. Varadi, S. Macavei, L. Barbu-Tudoran and C. Leostean, et al., Energy Fuels, 2024, 38, 19088–19099 CrossRef CAS.
- A. B. Djurišić, X. Chen, Y. H. Leung and A. M. C. Ng, J. Mater. Chem., 2012, 22, 6526–6535 RSC.
- G.-L. Li, S.-Y. Wu, X.-F. Hu, B.-H. Teng and M.-H. Wu, J. Appl. Spectrosc., 2016, 83, 374–378 CrossRef CAS.
- O. Volnianska, J. Chem. Phys., 2021, 154, 124710 CrossRef CAS PubMed.
- K. T. Lee, S. Jeong and J. Cho, Acc. Chem. Res., 2013, 46, 1161–1170 CrossRef CAS.
- R. Danesi, Laurea a ciclo unico, 2018, 8236 Search PubMed.
- M. Q. Alfaifi and A. A. Bagabas, Adv. Mater. Sci., 2019, 4, 1–10 Search PubMed.
- X. Shao, D. Zhang, M. Tang, H. Zhang, Z. Wang, P. Jia and J. Zhai, Chem. Eng. J., 2024, 495, 153676 CrossRef CAS.
- M. M. Khan, S. Kumar, A. N. Alhazaa and M. Al-Gawati, Mater. Sci. Semicond. Process., 2018, 87, 134–141 CrossRef CAS.
- X. Guo, J. Duan, C. Li, Z. Zhang and W. Wang, J. Mater. Sci., 2020, 55, 2018–2031 CrossRef CAS.
- M. Sher, M. Javed, S. Shahid, S. Iqbal, M. A. Qamar, A. Bahadur and M. A. Qayyum, RSC Adv., 2021, 11, 2025–2039 Search PubMed.
- Y. Wang, R. Shi, J. Lin and Y. Zhu, Energy Environ. Sci., 2011, 4, 2922–2929 Search PubMed.
- D. Sudha, E. R. Kumar, S. Shanjitha, A. M. Munshi, G. A. Al-Hazmi, N. M. El-Metwaly and S. J. Kirubavathy, Ceram. Int., 2023, 49, 7284–7288 Search PubMed.
- V. Mursyalaat, V. Variani, W. Arsyad and M. Firihu, J. Phys.:Conf. Ser., 2023, 012042 CrossRef CAS.
- D. Toloman, A. Popa, M. Stefan, O. Pana, T. D. Silipas, S. Macavei and L. Barbu-Tudoran, Mater. Sci. Semicond. Process., 2017, 71, 61–68 CrossRef CAS.
- B. Chander Joshi and A. K. Chaudhri, ACS Omega, 2022, 7, 21877–21881 Search PubMed.
- M. Masar, H. Ali, A. C. Guler, M. Urbanek, P. Urbanek, B. Hanulikova, H. Pistekova, A. Annusova, M. Machovsky and I. Kuritka, Colloids Surf., A, 2023, 656, 130447 CrossRef CAS.
- D. Toloman, A. Popa, M. Stefan, T. D. Silipas, R. C. Suciu, L. Barbu-Tudoran and O. Pana, Opt. Mater., 2020, 110, 110472 CrossRef CAS.
- C. Xia, F. Wang and C. Hu, J. Alloys Compd., 2014, 589, 604–608 CrossRef CAS.
- Z. Ma, F. Ren, X. Ming, Y. Long and A. A. Volinsky, Materials, 2019, 12, 196 CrossRef CAS PubMed.
- I. Idrees, A. Razzaq, M. Zafar, A. Umer, F. Mustafa, F. Rehman and W. Y. Kim, Arabian J. Chem., 2024, 17, 105615 CrossRef CAS.
- A. Yavuz, D. Aydin, B. Disli, T. Ozturk, B. Gul, I. H. Gubbuk and M. Ersoz, Environ. Sci. Pollut. Res., 2024, 31, 44828–44847 CrossRef CAS PubMed.
- Q. Xiang, J. Yu and M. Jaroniec, J. Phys. Chem. C, 2011, 115, 7355–7363 Search PubMed.
- H. Wang, X. Zhang, J. Xie, J. Zhang, P. Ma, B. Pan and Y. Xie, Nanoscale, 2015, 7, 5152–5156 RSC.
- R. Mekkat, E. M. Kutorglo, M. Setka, A. Prokhorov and M. Šoóš, J. Photochem. Photobiol., A, 2025, 116454 Search PubMed.
- M. Sakkaki and S. M. Arab, Synth. Sintering, 2022, 2, 176–180 CrossRef.
- T. Suter, V. Brázdová, K. McColl, T. S. Miller, H. Nagashima, E. Salvadori, A. Sella, C. A. Howard, C. W. Kay and F. Corà, et al., J. Phys. Chem. C, 2018, 122, 25183–25194 Search PubMed.
- D. S. Patrick, A. Govind, P. Bharathi, M. K. Mohan, S. Harish, J. Archana and M. Navaneethan, Appl. Surf. Sci., 2023, 609, 155337 CrossRef.
- D. Toloman, A. Popa, M. Stan, M. Stefan, G. Vlad, S. Ulinici, G. Baisan, T. D. Silipas, S. Macavei and C. Leostean, et al., J. Alloys Compd., 2021, 866, 159010 CrossRef CAS.
- A. U. Ammar, I. D. Yildirim, M. H. Aleinawi, M. Buldu-Akturk, N. S. Turhan, S. Nadupalli, A. M. Rostas and E. Erdem, Mater. Res. Bull., 2023, 160, 112117 CrossRef CAS.
- P. Xia, B. Cheng, J. Jiang and H. Tang, Appl. Surf. Sci., 2019, 487, 335–342 CrossRef CAS.
- B. Babu, T. Aswani, G. T. Rao, R. J. Stella, B. Jayaraja and R. Ravikumar, J. Magn. Magn. Mater., 2014, 355, 76–80 CrossRef CAS.
- D. R. Lorenz, J. R. Wasson, P. R. Johnson and D. A. Thornton, J. Inorg. Nucl. Chem., 1975, 37, 2297–2302 Search PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- W. Hagen, Practical approaches to biological inorganic chemistry, Elsevier, 2020, pp. 121–154 Search PubMed.
- Y. Gogotsi and R. M. Penner, Energy storage in nanomaterials-capacitive, pseudocapacitive, or battery-like?, 2018 Search PubMed.
- J. P. A. dos Santos, F. C. Rufino, J. I. Y. Ota, R. C. Fernandes, R. Vicentini, C. J. Pagan, L. M. Da Silva and H. Zanin, J. Energy Chem., 2023, 80, 265–283 Search PubMed.
- W. K. Chee, H. N. Lim, I. Harrison, K. F. Chong, Z. Zainal, C. H. Ng and N. M. Huang, Electrochim. Acta, 2015, 157, 88–94 CrossRef CAS.
- N. G. Hörmann and K. Reuter, J. Phys.: Condens. Matter, 2021, 33, 264004 CrossRef.
- H. Zhu, Y. Li, Y. Song, G. Zhao, W. Wu, S. Zhou, D. Wang and W. Xiao, Mater. Technol., 2020, 35, 135–140 Search PubMed.
- D. A. Bograchev, Y. M. Volfkovich and S. Martemianov, J. Electroanal. Chem., 2023, 935, 117322 CrossRef CAS.
- M. Alexandreli, C. B. Brocchi, D. M. Soares, W. G. Nunes, B. G. Freitas, F. E. de Oliveira, L. E. C. A. Schiavo, A. C. Peterlevitz, L. M. da Silva and H. Zanin, J. Energy Storage, 2021, 42, 103052 CrossRef.
- W. Pholauyphon, P. Charoen-Amornkitt, T. Suzuki and S. Tsushima, Electrochem. Commun., 2024, 159, 107654 CrossRef CAS.
- P. Widiatmoko, N. Nugraha, H. Devianto, I. Nurdin and T. Prakoso, IOP Conf. Ser.:Mater. Sci. Eng., 2020, 012040 CAS.
- A. C. Lazanas and M. I. Prodromidis, ACS Meas. Sci. Au, 2023, 3, 162–193 CrossRef CAS.
- M. Y. Perdana, B. A. Johan, M. Abdallah, M. E. Hossain, M. A. Aziz, T. N. Baroud and Q. A. Drmosh, Chem. Rec., 2024, 24, e202400007 Search PubMed.
- Y. Shao, M. F. El-Kady, J. Sun, Y. Li, Q. Zhang, M. Zhu, H. Wang, B. Dunn and R. B. Kaner, Chem. Rev., 2018, 118, 9233–9280 CrossRef CAS PubMed.
- A. Singh and A. Chandra, Enhancing specific energy and power in asymmetric supercapacitors-a synergetic strategy based on the use of redox additive electrolytes, Sci. Rep., 2016, 6, 25793 CrossRef CAS PubMed.
- I. Shaheen, K. S. Ahmad, C. Zequine, R. K. Gupta, A. G. Thomas and M. Azad Malik, Environ. Technol., 2022, 43, 605–616 CrossRef CAS.
- A. U. Ammar, F. Bakan-Misirlioglu, M. H. Aleinawi, G. Franzo, G. G. Condorelli, F. N. T. Yesilbag, Y. O. Yesilbag, S. Mirabella and E. Erdem, Mater. Res. Bull., 2023, 165, 112334 CrossRef CAS.
- S. Surender, M. Kavipriyah and S. Balakumar, Inorg. Chem. Commun., 2023, 150, 110557 CrossRef CAS.
- S. Ahlawat and S. Lata, Mater. Res. Bull., 2023, 165, 112328 CrossRef CAS.
- L. M. Jose, N. S. George, S. A. Kadam, D. Nayana and A. Aravind, Inorg. Chem. Commun., 2025, 178, 114527 Search PubMed.
- A. Kumar, H. Mittal and M. Khanuja, J. Energy Storage, 2023, 67, 107496 Search PubMed.
- C. Harak, V. Kadam, R. Gavhane, S. Balgude, A. Rakshe, N. Brahmankar, S. Uke, D. Satpute, H. Pawar and S. Mardikar, RSC Adv., 2024, 14, 4917–4929 RSC.
- L. G. Ghanem, M. A. Hamza, M. M. Taha and N. K. Allam, J. Energy Storage, 2022, 52, 104850 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |