 Open Access Article
Open Access ArticleTailoring Yb3+ energy levels by local configuration in the garnet structure: the case of Ca3(NbGa□)5O12 laser single crystals as a model for Yb:YAG
María Dolores Serrano a,
Concepción Cascales
a,
Concepción Cascales a,
Carlos Zaldo
a,
Carlos Zaldo *a,
Nicolas Trcerab,
João Elias F. S. Rodrigues
*a,
Nicolas Trcerab,
João Elias F. S. Rodrigues c,
Giulio Gorni
c,
Giulio Gorni d,
Mamoru Kitaura
d,
Mamoru Kitaura e and
Hirokazu Masai
e and
Hirokazu Masai f
f
aInstituto de Ciencia de Materiales de Madrid, Consejo Superior de Investigaciones Científicas, c/Sor Juana Inés de la Cruz 3, 28049 Madrid, Spain. E-mail: cezaldo@icmm.csic.es
bSynchrotron Soleil, 91192 Gif-sur-Yvette Cedex, France
cSynchrotron ALBA, Carrer de la Llum 2, 26, Cerdanyola del Vallès, 08290 Barcelona, Spain
dInstituto de Cerámica y Vidrio. Consejo Superior de Investigaciones Científicas, c/Kelsen 5, 28049 Madrid, Spain
eFaculty of Science, Yamagata University, Yamagata, 990-8560, Japan
fDepartment of Materials and Chemistry, National Institute of Advanced Industrial Science and Technology (AIST), Osaka, 563-8577, Japan
First published on 2nd January 2026
Abstract
Crystallographic information on the cationic interactions that may broaden the Yb3+ optical bands in garnets for sustaining shorter femtosecond laser pulses is provided. It is shown that the energy of the Yb3+ 2F7/2(0) ↔ 2F5/2(0′) optical absorption (0 ↔ 0′ OA), measured at a cryogenic temperature (T = 6 K) in Ca3(NbGa□)5O12 (CNGG)-type disordered single-crystal garnets, is sensitive to the electric charge of the cations incorporated in the 24d tetrahedral site, while it is much less sensitive to substitutions made on the 16a octahedral site. CNGG single-crystals nominally doped with 8 at% of Yb and further modified with other optically silent cations were grown by the Czochralski method. Li+, Mg2+, Ge4+, and Ti4+ were successfully incorporated into the crystals. Further, Yb-doped CNGG crystals grown in the composition limits for congruent melting were studied to explore the effect of a change in the cationic vacancy density. The lattice position of the three latter cations is unequivocally determined by the combined analyses of X-ray absorption spectroscopy (XAS) and single-crystal X-ray diffraction (scXRD) refinements. Li+ and Ge4+ exclusively fill the tetrahedral garnet site, with a strong reduction in the cationic vacancy density monitored in the Li case by positron annihilation lifetime spectroscopy (PALS). Ti4+ sits exclusively in the octahedral garnet site with no effect on the crystal cationic vacancy density, while Mg2+ is distributed in the three garnet sites with preference for the tetrahedral one and a moderate reduction in the crystal vacancy density. The Yb3+ 0 ↔ 0′ OA bands observed at λ = 973 nm, 971.9 nm, 971.3 nm, 971.1 nm and 969.6 nm are correlated with the presence of a vacancy (electric charge Q = 0), Li+, Mg2+, Ga3+ and Ge4+ in the tetrahedral garnet sites nearest to Yb3, respectively. However, the incorporation of Ti4+ in the octahedral site substituting mainly Ga3+ has no observable effect on the Yb3+ 0 ↔ 0′ OA. The elimination of tetrahedral cationic vacancies slightly reduces the Yb3+ 300 K luminescence bandwidth in the Li+- and Mg2+-modified CNGG crystals, while the new energy levels associated with the tetrahedral Ge4+ compensate for this effect and slightly increase it.
1 Introduction
The generation of ultrashort laser pulses requires active media with a large optical emission bandwidth.1 Additionally, other favourable physical properties of the media, namely, high thermal conductivity, favourable thermo-mechanical properties and low anisotropy, are also required for efficient laser operation.Trivalent lanthanides (Lns), with an [Xe]4fn electronic configuration, have much smaller optical (absorption and emission) bandwidths than transition metal ions, for instance Ti3+ ([Ar]3d1), because the host crystal field (CF) on the f orbitals is shielded by the outer, although less energetic, 5s and 5p orbitals of Lns. However, Lns that can be resonantly pumped with infrared semiconductor diode lasers (DL) have attracted great attention as laser centres due to the fact that they have a low energy difference between the absorbed and emitted photons (low quantum defect), and thus, the heat transferred to the host is minimised, allowing the output laser intensity to be scaled up.
In comparison to other laser Lns, the near-to-full electronic configuration of Yb3+([Xe]4f13) has the strongest interaction with the host lattice vibrations, resulting in intrinsically larger optical absorption and emission bandwidths than the other Lns. Yb3+ has received a lot of attention as an in-band DL pumped mode-locked laser system.2 Although many different glasses and single crystals have been tested as Yb3+ hosts, the cubic Y3Al5O12 (YAG) garnet remains the workhorse for industrial laser systems in most cases because it possesses the aforementioned favourable physical properties; however, the narrow laser gain bandwidth (even shorter than the fluorescence bandwidth) of Yb3+ in YAG, i.e. ≈8 nm at λ = 1030 nm, limits the laser pulse duration to ≈140 fs.3
Fig. S1a in the SI sketches the structural units of garnet lattice with the generic formula {A}3[B]2(C)3O12. A, B and C correspond to the 8-fold oxygen-coordinated cations at the dodecahedral (24c) position, 6-fold oxygen-coordinated cations in the octahedral centrosymmetric (16a) site, and 4-fold oxygen-coordinated cations at the tetrahedral (24d) site, respectively. Different cations with diverse oxidation states can occupy these sites, giving rise to a plethora of garnet compounds. In YAG, yttrium and dopant Lns fill the 24c site, while aluminium fills both the 16a and 24d lattice sites.
Given that the energy of the Yb3+ electronic levels is determined by the strength and symmetry of the CF on the Yb3+ site, attempts to enlarge the Yb (and other Ln) optical bandwidths in YAG indeed have been pursued by partially or fully replacing Y3+ and Al3+ with other optically-silent isovalent cations, e.g. Gd3+, Lu3+, Sc3+, and Ga3+. In this approach, changes in the CF rely on the strain of the garnet lattice due to the ionic radius mismatch (Δr = (r2 − r1)/r1) between the replaced ions (r1 for Y or Al) and the new ones introduced (r2). Fig. S1a graphically shows the common occupancy sites as a function of the ionic radius and site coordination, and Table S1 summarises the ionic radius mismatches for common substitutions in garnets. The possible cationic environments around the 24c garnet site of Yb3+ are shown in Fig. S1b.
According to the published 300 K photoluminescence data, the most intense Yb3+ emission in YAG at λ = 1030 nm has a fluorescence bandwidth with a full width at half maximum of FWHM = 85 cm−1.4 If dodecahedral Y3+ (rY,CN=8 = 1.019 Å) is fully replaced by isovalent Lu3+ (rLu,CN=8 = 0.977 Å), the fluorescence bandwidth is reduced to FWHM = 56.2 cm−1,5 which is a small change likely due to the very small Y/Lu radius mismatch, i.e. Δr = −0.0412. When the octahedral Al3+ (rAl,CN=6 = 0.535 Å) is replaced by Sc3+ (rSc,CN=6 = 0.745 Å, i.e. ΔrAl–Sc,CN=6 = 0.392), the fluorescence bandwidth increases up to FWHM = 127 cm−1.4 Alternatively, the full replacement of octahedral and tetrahedral Al3+ with Ga3+ leads to an emission bandwidth of only FWHM = 102 cm−1,6 which could be associated with the smaller radius mismatches induced in both sites with regard to the previous case, i.e. ΔrAl–Ga,CN=6 = 0.159 and ΔrAl–Ga,CN=4 = 0.205. It is seen that the isovalent replacement strategy induces a limited change in the Yb3+ fluorescence bandwidth in YAG-like laser garnets. Thus, it is necessary to understand the physical interactions in the garnet structure to maximise the Ln optical bandwidths.
Other garnet families combine heterovalent substitutions over two sites of the garnet structure. For instance, Ca3Sc2Ge3O12 compensates the extra Ge4+ charge (with regard to Al3+) in the tetrahedral site with Ca2+ charge deficit (with regard to Y3+) in the dodecahedral site, basically remaining an “ordered” lattice, i.e. each 24c, 16a or 24d garnet site is occupied by a unique A, B or C cation type. In this host, the 300 K fluorescence bandwidth of the Yb3+ emission at λ = 1031 nm is FWHM = 73 cm−1,7 i.e. no fluorescence bandwidth enhancement with regard Yb:YAG is found.
In contrast to the above-mentioned approaches, the introduction of heterovalent substitutions, along with the concept of crystal cationic disorder, i.e. the same crystal site shared by at least two cations with different electric charges and sizes, in the Ca3(NbGa□)5O12 (CNGG, □ stands for cationic vacancies) single crystal produced the largest Yb3+ fluorescence bandwidth reported thus far in a single crystal garnet, namely, FWHM = 220.6 cm−1 for the λ = 1027.5 nm emission band.8,9
In the CNGG single crystal (and in related compositions grown after host modification with Li+ or Na+ ions), Na+, Ca2+ and Yb3+ share the dodecahedral site, while Nb5+ and Ga3+ are simultaneously distributed over the octahedral (preferential for Nb5+ with occupancy factor OF = 0.625) and tetrahedral (preferential for Ga3+, OF = 0.821) lattice positions.10 Furthermore, Li+ exclusively occupies the tetrahedral position, removing cationic vacancies at this site.11 At the local level, the cationic distribution around Yb3+ is random but with given probabilities from the macroscopic point of view. In this case, the CF on Yb3+ is determined not only by the change in the Yb–O bonding distance but also by the oxidation state of other surrounding cations, i.e., the total electric charge around Yb3+. This is the ultimate reason for the large enhancement in the Yb3+ fluorescence bandwidth in CNGG with regard to other garnets.
The CNGG capability to incorporate foreign cations, often in excess of 10% of the corresponding site occupancy, gives the unique opportunity for the study of the influence of the cationic size and charge modification in the garnet structure in the spectroscopy of Lns. Yb3+ is selected in the present study because of its largest sensitivity to the lattice environment. To unambiguously determine the impact of structural changes on the optical spectroscopy of Yb3+, we focused our study on the 2F7/2(0) ↔ 2F5/2(0′) transition (shortly 0 ↔ 0′) monitored at low temperature (T = 6 K) with a high spectral resolution (<0.2 nm), which effectively eliminates the thermal effects observed in spectroscopic measurements conducted at room temperature (RT).
The purpose of the present work is to examine the effect of the incorporation in the octahedral and tetrahedral garnet sites (shortest intercationic distances with the dodecahedral site, see SI Table S3) of optically silent cations (Li+, Mg2+, Ge4+ and Ti4+) with increasing electric charge (Q) but ionic radius not very different from that of Nb5+ and Ga3+ for each corresponding coordination; see SI Table S2. We intend to reach conclusions about how to modify the energy of the Yb3+ levels by a proper combination of cations, which in the end may give rise to the operation of garnet hosts, such as YAG, LuAG, and GGG, in the ultrashort (<100 fs) laser pulse duration regime.
A major uncertainty to reach conclusions in this respect is the lack of unequivocal knowledge of the site occupied by the cations used for lattice modification. To address this point, we use a combination of X-ray absorption near edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) spectroscopies for Mg2+, Ti4+, and Ge4+ cations and single crystal X-ray diffraction (scXRD) analyses for all the studied crystals.
The vacancies present in the three cationic sites of the CNGG garnet provide zero electric charge (Q = 0) on these sites. It is known that in ≥5 at% Yb-doped CNGG, the dodecahedral vacancies disappear, while their density in the octahedral site is significantly reduced. Only vacancies in the tetrahedral site remain in a significant concentration after Yb doping.10,11 Even without any experimental proof, some authors postulate than Li+ is incorporated in the octahedral garnet site,12 despite the fact that firm experimental evidence of the incorporation of Li+ exclusively in the tetrahedral garnet site and strong reduction of the corresponding cationic vacancies was previously provided.11 To get a deeper insight into the role of the different crystal modifiers on the cationic vacancy density, we now provide further evidence of their evolution by positron annihilation lifetime spectroscopy (PALS).
2 Experimental techniques
2.1. Crystal growth
Pure and modified 8 at% Yb:CNGG single crystals were grown in air using the Czochralski technique and a Cyberstar puller. Garnet powders obtained by solid-state synthesis (SSS) were melted in Pt crucibles. Details of SSS can be found in the SI, Section S2, and details of the CNGG crystal growth procedures can be found in our previous works.10,11,13 CNGG modifications with Li, Mg, Si, Ge, Ti and V were attempted, but successful crystal growth and cationic incorporation into the garnet lattice were possible only for Li, Mg, Ge and Ti modifiers. The presence of Li in the crystal was assessed in a previous work using NMR and neutron diffraction analyses.11 The incorporation of Yb as well as Mg, Ge and Ti modifier cations into the single-crystal garnet lattice was qualitatively confirmed by energy dispersed X-ray fluorescence (EDX) using an EDAX Genesis XM2i probe in a FEI Nova Nano SEM230 scanning electron microscope; see Fig. S7 of Section S3. Further, the content of the different elements was found directly in the crystals by X-ray fluorescence analyses (XFA) in a JEOL Superprobe JXA-8900 Electron Probe Micro Analyser (EPMA). The ZAF method14 and corresponding elemental standards, CaO, Nb2O5, Ga2O3, Yb2O3, MgO, GeO2 and TiO2, were used. Given that the segregation coefficient (ratio between atomic crystal and melt compositions) of Yb is near to one,11,13 for simplicity the melt crystal composition is used to name the samples. The segregation coefficients of Ge and Ti were found to be 0.4 and 0.96 assuming tetrahedral and octahedral site occupancies, respectively (see later sections).Two 8 at% Yb:CNGG crystals with 10 at% and 20 at% Si substitution of Ga in the initial charge were grown. The transparency of these crystals was poor; see in SI Fig. S3d and EDX and EMPA analyses show that Si is incorporated in a very small amount, with a segregation coefficient of 0.15. Further, crystal regions with a low Ga content were observed; thus, these solidified materials were not a single phase. The growth of 15 at% V-modified 8 at% Yb:CNGG produced a garnet single crystal, but EDX and EPMA analyses showed that V is not incorporated into the garnet lattice; see SI Fig. S7f.
2.2. Positron annihilation lifetime spectroscopy
Positron annihilation lifetime spectroscopy (PALS) was performed using a positron surface analyser PSA TypeL-II (Toyo Seiko Co., Ltd) adopting an anticoincidence processing system.15 A 22Na source, which was encapsulated with Kapton® film, was used for measurement. The accumulated counts for each sample was 107.Positron annihilation lifetimes and relative intensities were determined using the LT9 program for decay analyses.16 The apparatus response function (resolution function) and background signals were evaluated using stainless steel (CRM 5607-a) from the National Metrology Institute of Japan (NMIJN).
The experimental PALS spectrum Sex(t) is given by a convolution of the theoretical function S(t) with the resolution function R(t), as follows:
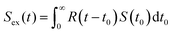 | (1) |
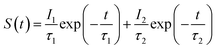 | (2) |
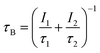 | (3) |
The values of τB are compared between experiments and calculations to validate whether they were carried out appropriately.18
2.3. X-ray absorption spectroscopy (XAS)
XANES and EXAFS spectra of Mg and Ti were collected at the LUCIA beamline of the SOLEIL synchrotron facility,19 with an injected electron energy and current of 2.75 GeV and 500 mA, respectively. XAS spectra were collected in fluorescence mode with a silicon drift diode detector applying a dead time correction. The bulk samples were put on graphite tape stuck on copper slides. The sample holder was rotated by 35° (for Mg K-edge) and 5° (for Ti K-edge) to increase the signal and minimise self-absorption effects as much as possible.Mg K-edge XAS spectra were obtained using a KTP(111) double-crystal monochromator for CNGG samples and a Multilayer Grazing Monochromator (MGM) for Mg-model compounds. The first inflection point of the Mg K-edge of periclase MgO at 1306.6 eV was used for energy calibration of the monochromator. XAS spectra were recorded over the energy range of 1270 to 1598 eV with variable energy steps of 2 eV between 1270 and 1298 eV; 0.2 eV between 1298.2 and 1333 eV; 0.5 eV between 1333.5 and 1450 eV; 1 eV between 1451 and 1550 eV and 2 eV between 1552 and 1598 eV. In all cases, a counting time of sixteen seconds per point was used. To increase the signal-to-noise ratio, a total of 16 spectra per sample were averaged.
Ti K-edge XAS spectra were collected using an Si(111) double crystal monochromator over an energy range of 4850 to 5998 eV, with steps of 2 eV from 4850 to 4956 eV; 0.2 eV from 4956.2 to 5000 eV; 0.5 eV from 5000.5 to 5085 eV; 1 eV from 5086 to 5500 eV and 2 eV from 5502 to 5998 eV. For each point, the counting time was three seconds. Two spectra were averaged to increase the signal-to-noise ratio. Metallic titanium foil was used to calibrate the monochromator at 4966 eV for the first inflection point of the spectrum.
Ge K-edge (11.103 keV) XAS experiments were performed in transmission mode at the BL22-CLÆSS beamline of CELLS-ALBA.20 A collimated beam with dimensions of 1(H) × 1(V) mm2 was used. The monochromatic beam was generated by a pair of Si(311) crystals. Finely ground powders were mixed with cellulose and pelletised into 5 mm diameter discs to achieve the optimal absorption edge jump. XAS data were collected across a k-range extending up to 14 Å−1 under ambient conditions, with a step scanning of 0.3 eV for XANES and 1 eV for EXAFS.
XAS spectra were collected both for modified Yb:CNGG single crystals and for the Ge or Ti reference crystals specifically grown for this purpose; see in SI, Section S4. In all cases, the EXAFS oscillations χ(k) were processed using the Athena software,21 which facilitated pre-edge background subtraction, edge jump normalisation, and extraction of the extended-range oscillations. Fourier transformation (FT) of the k-weighted k2·χ(k) oscillations was performed using a Hanning-type apodization function (Δk = 2 Å−1, ΔR = 2 Å) in both k- and R-spaces, with Δk ranging from 2 to 9.5 Å−1 and ΔR ranging from 1 to 4 Å.
2.4. X-ray diffraction (XRD)
The crystalline phases present in the SSS products and powdered single crystals were determined at RT by powder X-ray diffraction (XRD) 2θ = 10°–80° scans using a Bruker D8 Advance instrument with Cu Kα radiation (λ = 1.5406 Å).Crystal structures were determined from scXRD data collected at T = 296(2) K with a Bruker Kappa Apex II diffractometer equipped with a fine-focus sealed Mo tube working at 50 kV/30 mA. Kα radiation (λ = 0.71073 Å) was selected using a graphite monochromator. Small prismatic single crystals cut from the grown crystals were selected to minimise the possibility of twinning. Data were corrected for absorption using the multi-scan method (SADABS). All calculations were performed using the SHELXTL software.22 Structure refinements of all studied crystals were performed in the cubic space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d (no 230) characteristic of this structure. These refinements included the evaluation of the cationic and vacancy distributions over available dodecahedral (24c), octahedral (16a) and tetrahedral (24d) garnet sites.
d (no 230) characteristic of this structure. These refinements included the evaluation of the cationic and vacancy distributions over available dodecahedral (24c), octahedral (16a) and tetrahedral (24d) garnet sites.
2.5. Optical spectroscopy
The OA spectra of the Yb3+ 0 ↔ 0′ transition in the single crystals were determined at T = 6 K using an Agilent Technology spectrophotometer, model CARY5000. The samples were cooled with a closed cycle He cryostat. OA spectra were collected with a spectral bandwidth resolution better than 0.2 nm and the reported results are the average of at least twenty spectra.The excitation and emission spectra of Yb3+ fluorescence were measured. For the compositions whose crystal growth was not successful, SSS powders were dispersed in KBr pellets, and their excitation spectra were collected. Two-side polished plates were used for successfully grown crystals. In all cases, excitation was performed using a chopped Spectra Physics Ti-sapphire (Tisa) laser. The average Tisa laser power was always kept below 100 mW (<12.8 W cm−2) to minimise sample heating. The luminescence was dispersed by a Czerny–Turner SPEX (model 340E, f = 34 cm) monochromator and detected by a 77 K cooled Ge photodiode using a lock-in amplifier. The spectral resolution of the excitation spectra was determined by the Tisa laser emission bandwidth, i.e. 0.05 nm.
3. Experimental results
3.1. Q = 0: cationic vacancies in CNGG single crystals
It is worth noting that to grow CNGG single crystals from congruent melts, the composition of the precursor powder must deviate from the stoichiometric garnet composition; namely, a cation-deficient Ca3Nb(1.5+1.5x)Ga(3.5−2.5x)□xO12 composition with x = 0.11–0.14 is required. Most often, the Ca3Nb1.6875Ga3.1875O12 (x = 0.125) composition is used for the Czochralski crystal growth of CNGG.23,24 To date, several works have studied the crystal cationic composition using X-ray or neutron diffraction techniques.10,11,13,25,26 Beyond experimental uncertainties, two structural characteristics are concluded in all works, as follows: (a) Nb5+ and Ga3+ share the 16a and 24d garnet sites and (b) cationic vacancies are found in the three garnet sites, particularly significant in the tetrahedral 24d site (up to ≈8% of the site population). Given that the electric neutrality of this CNGG formulation is based in the cationic/anionic balance (independently of x), these vacancies provide zero electric charge on the corresponding site.Thus far, the evaluation of the crystal cationic vacancy composition has been indirectly obtained from the cationic composition. Alternatively, we used PALS as a direct method for monitoring the presence of crystal vacancies upon the introduction of Yb dopant and other cations used here to modify the crystalline lattice.
 | ||
| Fig. 1 Room temperature PALS spectra of (a) CNGG, (b) CLNGG, (c) 8 at% Yb:CNGG, and (d) 8 at% Yb:CLNGG. Red solid circles are the experimental data. Blue dashed lines are the components used to fit the experimental data using the two-state trapping model given by eqn (2). The sum of the blue dashed lines is indicated by a green solid line. The insets show the same results in a semilogarithmic representation. | ||
| Crystal | τ1 (ps) | I1 (%) | τ2 (ps) | I2 (%) | τB (ps) |
|---|---|---|---|---|---|
| CNGG | — | — | 246 ± 1 | 100 | — |
| 8 at% Yb:CNGG | 50.5 ± 0.7 | 9.4 ± 1.2 | 246 ± 1 | 90.6 ± 1.2 | 180 ± 11 |
| 10 at% Ti:8 at% Yb:CNGG | 58.8 ± 9.3 | 11.1 ± 1.3 | 246 ± 1 | 88.9 ± 1.3 | 182 ± 12 |
| 30 at% Mg:8 at% Yb:CNGG | 67.0 ± 10.0 | 13.9 ± 1.1 | 249 ± 1 | 86.1 ± 1.1 | 181 ± 12 |
| CLNGG | 67.8 ± 4.9 | 16.6 ± 0.7 | 237 ± 1 | 83.4 ± 0.7 | 167 ± 6 |
| 8 at% Yb:CLNGG | 59.0 ± 7.0 | 15.6 ± 1.1 | 236 ± 1 | 84.4 ± 1.1 | 160 ± 9 |
The PALS spectrum of CNGG can be fit with a single exponential decay function in eqn (2), while that of any other CNGG crystal studied here requires the sum of two exponential decay functions. The slow decay component of Li-modified CNGG (CLNGG) is regarded as having the same origin as the decay component of CNGG because their lifetimes are close to each other. The lifetime values determined are consistent with the calculated positron annihilation lifetimes either at the 16a or 24d garnet sites in LuAG.18 This fact indicates that in undoped CNGG, positrons predominantly annihilate at these vacant sites, but in CLNGG, the intensity of the slow decay component is weakened by the occurrence of a fast decay component, suggesting that Li+ doping reduces the cation vacancy density at these sites.
To verify the effect of Li+ doping on the suppression of these cation vacancies in Yb-doped CNGG, the PALS spectra of 8 at% Yb:CNGG and 8 at% Yb:CLNGG are compared. The PALS spectra of these materials are also composed of two exponential decay functions, as shown in Table 1. The τ2 values of Yb:CNGG and Yb:CLNGG are similar. Thus, it seems likely that positrons are trapped at the same cation vacancies as in CNGG and CLNGG. The I2 value decreases in Yb:CLNGG compared to Yb:CNGG. This feature was also seen in the comparison of CNGG and CLNGG, indicating that Li+ doping always plays an active role in removing cation vacancies in CNGG.
It may be noted that Yb3+ doping of CNGG also reduces the I2 value. The possibility that this situation could be associated with the Yb3+ antisite in the 16a octahedral positions, as found for other garnet constituents (Fe, Ga, Y, Gd or Er),29 seems unlikely in the CNGG case. In fact, this Yb3+ antisite in the octahedral 16a site has been evidenced by the presence of dipolar magnetic optical transitions in 0.3 at% Yb:CNGG crystals30 but the Yb solubility limit in the octahedral site is very low, ≈5 × 1018 cm−3, and it cannot account for the strong I2 reduction observed.
Further, the effect of Mg2+ and Ti4+ codoping on the 16a and 24d cation vacancies of CNGG was monitored by PALS. The value of I2 in 8 at% Yb:CNGG decreases upon Mg2+ codoping, as in the case of Li+ codoping. However, Mg2+ codoping is not as effective as Li+ in reducing the 16a or 24d cationic vacancies because, as will be shown later, Mg2+ is distributed in the three garnet lattice sites. Conversely, the value of I2 in 8 at% Yb:CNGG is not changed by Ti4+ codoping. Clearly, the incorporation of Ti4+ into Yb:CNGG has little effect on cation vacancies at 16a and 24d sites.
Based on the PALS experiments alone, it is difficult to identify which cationic vacancies are removed by the incorporation of Yb3+, Li+, Mg2+, or Ti4+ into CNGG. In fact, the τ2 values calculated using a two-component density functional theory for LuAG are close each other, i.e. 274 ps, 239 ps and 233 ps for 24c, 16a and 24d, respectively.18 To get a clearer picture of the crystallographic changes induced by these cationic incorporations, we present the XAS and scXRD results in following sections.
Other bands at longer wavelengths (lower energy) than that of the 0 ↔ 0′ one are observed at T = 300 K, for λ > 975 nm. These bands completely disappear by lowering the sample temperature to 6 K, and thus they are ascribed to transitions from the excited Stark mJ sublevels of the ground 2F7/2 multiplet, which are populated due to the Boltzmann electronic distribution, i.e., 2F7/2 (1, 2, 3) → 2F5/2 (mJ) transitions. Their spectral overlap with the 0 → 0′ OA band at T = 300 K compromises the proper resolution of the features associated with the inhomogeneous broadening in the disordered CNGG lattice, i.e. different lattice environments around Yb3+. Owing to this reason, spectroscopy at T = 6 K is required to disclose the effects of this disorder.
Fig. 2b shows the OA of Yb3+ in CNGG measured at T = 6 K exclusively for the 0 → 0′ transition region. It shows several contributions ascribed to different Yb3+ environments, whose assignment is the purpose of the present work. The most intense band at λ = 971.1 nm should correspond to 24c Yb3+ in the most abundant garnet lattice environment, i.e. with 24c Ca (× 4), 16a Nb (× 4) and 24d Ga (× 4 + 2) occupancies, see in SI Fig. S1b and Table S2, while the side band at λ = 973 nm reveals the presence of some lattice modification in the Yb3+ environment. It is worth noting that the relative intensity of the λ = 973 nm band has a tendency to increase as the crystal grows, i.e. its intensity is generally found to be higher at the final part of the crystal than in its initial part, as shown in Fig. S13b. This behaviour could be induced by the loss of gallium with crystal growth, as evidenced in Fig. S12a. This Ga loss also suggests a slight increase in the 24d tetrahedral vacancy density given that Ga is the most abundant cation in this site and the relative enrichment in Nb5+ must be compensated to maintain charge neutrality.
3.2. Q = +1: Li+-modified Yb:CNGG single crystal
Li-modified CNGG crystals (CLNGG) have been grown from melts with the composition Ca3Nb1.775Ga2.95Li0.275□0.025O12, i.e. closer to the stoichiometric garnet formula than in the congruent CNGG case. According to the previously published combined NMR, neutron diffraction, and scXRD analysis, it was concluded that Li enters exclusively in the 24d tetragonal garnet site and that the vacancy density in this site decreases strongly upon the incorporation of Li.11 The PALS results, as described in Table 1, also show that the incorporation of Li is the most effective way to reduce the presence of cationic vacancies remaining in CNGG after 8 at% Yb doping.Fig. 3a shows a comparison between the 0 → 0′ OA of Yb3+ measured at T = 6 K in CNGG and in CLNGG. The most significant difference between these two spectra is the drastic reduction in the intensity of the λ = 973 nm OA band upon the incorporation of Li+. Further, a band that is not fully resolved appears as a shoulder at λ ≈ 971.9 nm.
Considering that the cationic vacancies on the 24c site are removed by the substitution of Ca2+ by Yb3+ (thus they are not present in 8 at% Yb:CNGG) and that cationic vacancies in the 16a site are near zero in all cases,10,11 as also shown in Table 3, the main effect of Li incorporation is the reduction of the tetrahedral 24d vacancy concentration from the OF ≈ 0.075 in 5–15 at% Yb:CNGG to only OF = 0.009 in 8 at% Yb:CLNGG, which is further confirmed by the presented PALS results. Thus, we tentatively correlate both facts and ascribe the Yb3+ OA band at λ = 973 nm to the specific CF created by a Yb surrounding configuration containing a 24d tetrahedral vacancy □TET, i.e. Q = 0, as the first cationic neighbour. In the same manner, the new shoulder at λ ≈ 971.9 nm could be ascribed to a CF including a nearest 24d tetrahedral Li+, Q = 1, close to Yb3+.
3.3. Q = +2: Mg2+-modified 8 at% Yb:CNGG single crystals
Garnets with stoichiometric concentrations of magnesium in dodecahedral, {Mg3}[Al2](Si3)012 (pyrope), octahedral, {Gd3}[Mg2](GaGe2)012, {Ca3}[TiMg](Ge3)012, {Ca3}[ZrMg](Ge3)012, {Y3}[MgAl](Al2Si)O12 or distributed in both positions, {MgGd2}[Mg2](Ge3)012, have been reported in the literature.32,33 The low electronic density of Mg2+ makes the analysis of its crystalline lattice distribution quite unreliable using exclusively X-ray diffraction measurements. Owing to this reason, we first analyse the XAS of Mg-modified CNGG crystals to determine the garnet sites occupied by Mg and later we refine the scXRD results.The Mg K-edge XANES is usually described by three main features in the energy range of 1305–1320 eV labelled with increasing energy as A, B and C, followed by broader and weaker peaks between ≈1323 and ≈1331 eV, labelled as D. Also, a very weak pre-edge peak labelled P is seen for the Mg CN = 8. The position of peaks A, B and C shifts towards a higher energy when the Mg CN increases. This has been used in previous works as a fingerprint of Mg coordination.35,36
The distinctive feature of the Mg K-edge XANES spectra in CNGG is that it simultaneously displays the characteristics of the three Mg coordinations. At least eight XANES peaks can be observed. The most intense A and C peaks of the spinel (Mg CN = 4) can be observed in CNGG at 1306.4 and ≈1318 eV, respectively. The intense B and C peaks of the diopside (Mg CN = 6) correspond to those observed in CNGG at 1313 and ≈1318 eV, respectively, with the latter being broader than in the reference due to the overlap of the CN = 4 and 6 oxygen coordinations. Finally, the A and B features of pyrope are also observed in CNGG at 1310 and 1313 eV, respectively.
Fig. 4b shows the normalised and weighted k2χ(k) experimental EXAFS spectrum of Mg K-edge in a 30 at% Mg-modified 8 at% Yb:CNGG crystal, and Fig. 4c shows its Fourier transform. The EXAFS fit was performed in the three possible cationic garnet sites by fixing CN = 4, 6 or 8 coordinations and leaving the Debye–Waller factors, σ2, free, as shown in SI Fig. S11. Although in all coordinations, the observed Mg–O bond length results are 1.92–1.93 Å, the fit obtained for CN = 6 or 8 provides σ2 > 10−2 Å2, which is unrealistic for crystal oxides, and the fit errors are significantly larger for CN = 6 and 8 than in the CN = 4 case; see SI, Table S3. Further, the Mg–O bond length determined in CNGG is consistent with the typical Mg–O distance found in CN = 4 coordination in the MgAl2O4 spinel,36,37 or in akermanite, Ca2MgSi2O7,38 i.e. 1.92 Å. In contrast, the Mg–O distances found for CN = 6 in diopside (Mg–O4 at 2.073 Å plus Mg–O2 at 2.147 Å)34,36,39 or for CN = 8 in pyrope (Mg–O4 2.198 Å plus Mg–O4 2.343 Å),34,36 are clearly larger.
Therefore, the combined XANES and EXAFS analyses clearly indicate a Mg2+ distribution in the three garnet sites, with the majority in the 24d tetrahedral site with an Mg–O bond length of 1.93(2) Å in the latter. Table S4 summarises the results of the EXAFS fit.
| 30 at% Mga | 20 at% Geb | 10 at% Tic | |
|---|---|---|---|
| a A total of 6300 frames were collected. The total exposure time was 3.5 h. The final cell constant a = 12.4892(3) Å was based on the refinement of the xyz-centroids of 4943 reflections with I > 20σ(I) for 9.232° < 2θ < 59.91°.b A total of 5507 frames were collected. The total exposure time was 7.65 h. The final cell constant a = 12.4159(3) Å was based on the refinement of the xyz-centroids of 9252 reflections with I > 20σ(I) for 8.040° < 2θ < 56.35°.c A total of 5507 frames were collected. The total exposure time was 7.65 h. The final cell constant a = 12.4720(3) Å was based on the refinement of the xyz-centroids of 9891 reflections with I > 20σ(I) for 8.004° < 2θ < 56.525°. | |||
| Temperature (K) | 296(2) | ||
| Wavelength (Å) | 0.71073 | ||
| Crystal system/space group | Cubic/Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d d |
||
| Unit cell dimensions | |||
| a = b = c (Å) | 12.4892(3) | 12.4165(2) | 12.4720(3) |
| α = β = γ (°) | 90 | ||
| Volume (Å3)/Z = 8 | 1948.07(5) | 1914.25(9) | 1940.03(9) |
| Calculated density (Mg m−3) | 4.584 | 5.004 | 4.852 |
| Absorption coefficient (mm−1) | 12.770 | 15.929 | 13.618 |
| Crystal size (mm3) | 0.116 × 0.076 × 0.052 | 0.147 × 0.104 × 0.04 | 0.16 × 0.04 × 0.03 |
| θ range for data collection (°) | 4.00–30.49 | 4.02–28.28 | 4.02–28.2 |
| Index ranges | −17 ≤ h, k, l ≤ 17 | −16 ≤ h, k, l ≤ 16 | −16 ≤ h, k, l ≤ 16 |
| Reflections collected | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 857 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 992 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 871 871 |
| Independent reflections [R(int)] | 254 [0.0878] | 205 [0.0427] | 207 [0.0489] |
| Completeness to θ = 28.28° | 100.0% | ||
| Refinement method | Full-matrix least-squares on F2 | ||
| Data/restraints/parameters | 254/3/27 | 205/2/23 | 205/2/23 |
| Goodness-of-fit on F2 | 1.063 | 1.404 | 1.257 |
| Final R indices [I > 2σ(I)] | |||
| R1 | 0.0151 | 0.0104 | 0.0131 |
| wR2 | 0.0365 | 0.0283 | 0.0456 |
| R indices (all data) | |||
| R1 | 0.0242 | 0.0118 | 0.0135 |
| wR2 | 0.0453 | 0.0289 | 0.0460 |
| Extinction coefficient | 0.0018(1) | 0.00132(6) | 0.0055(2) |
| Largest diff. peak/hole (e Å−3) | 0.329/−0.390 | 0.187/−0.192 | 0.359/−0.449 |
Firstly, it can be mentioned that the lattice parameter determined for the 30 at% Mg-modified 8 at% Yb:CNGG crystal is a = 12.4892 Å, i.e. larger than that corresponding to its Yb doping level, a = 12.4728 Å for 8 at% Yb:CNGG, but lower than in undoped CNGG, a = 12.4969 Å, as shown in SI Table S2. This suggests the incorporation of Mg in the garnet sites with a positive radius mismatch, i.e. 16a and 24d, as shown in SI Table S1.
The scXRD refinement provides the OF of Mg in the three garnet sites; see Table 3 and in SI Table S7. 75% of the total Mg is incorporated in the 24d site, where a positive radius mismatch Δr = +21.27% occurs, which is in qualitative agreement with the lattice parameter enlargement observed with respect to 8 at% Yb:CNGG, and thus it is not surprising that the EXAFS-derived Mg–O bond distance was larger than that expected from an 8 at% Yb:CNGG lattice. The rest of Mg is distributed 17% in the 24c site with Δr = −20.54% and 8% in the 16a site with Δr = +12.5%, partially counterbalancing the lattice distortions and limiting the lattice parameter increase.
| CNGG crystal composition | OF | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In melt (at%) | In crystala (at%) | 24c dodecahedral site | 16a octahedral site | 24d tetrahedral site | ||||||||||
| Yb | Ca | Yb | □DOD | Nb1 | Ga1 | □OCT | Ga2 | Nb2 | □TET | |||||
| a EPMA results.b In addition to the Nb amount.c With respect to the total cationic positions (Ca + Yb + Nb + Ga + Mg).d With respect to the total amount of Nb, Ga and Ge. The measured Ge concentration changes from 6 at% to 8 at% during crystal growth, and the given value is the average.e With respect to the total amount of Nb and Ti.f The measured Yb concentration changes from 8 at% to 10 at% during crystal growth, and the given value is the average.g With respect to the 16a site occupancy. Data are very similar to (e) hypothesis because Ti and most of Nb are in the 16a site. The measured Ti concentration changes from 9.3 at% to 11 at% during crystal growth, and the given value is the average. | ||||||||||||||
| Undoped CNGG | 0.985 | 0.015 | 0.625 | 0.372 | 0.003 | 0.821 | 0.102 | 0.077 | ||||||
| 8 at% Yb:CNGG | 9.1 | 0.939 | 0.058 | 0.003 | 0.580 | 0.420 | 0.905 | 0.020 | 0.075 | |||||
| 11.6 at% Yb:CNGG | 12.7 | 0.900 | 0.100 | 0.579 | 0.421 | 0.877 | 0.048 | 0.075 | ||||||
| 15 at% Yb:CNGG | 18.8 | 0.838 | 0.157 | 0.005 | 0.627 | 0.371 | 0.002 | 0.921 | 0.005 | 0.074 | ||||
| Li | ||||||||||||||
| CLNGG | 0.998 | 0.002 | 0.66 | 0.34 | 0.842 | 0.052 | 0.080 | 0.026 | ||||||
| 8 at% Yb:CLNGG | 7.57 | 0.931 | 0.069 | 0.67 | 0.33 | 0.810 | 0.069 | 0.111 | 0.009 | |||||
| Mgc | Mg | Mg | Mg | |||||||||||
| 30 at% Mgb:8 at% Yb:CNGG | 7 | 5.8 | 0.900 | 0.060 | 0.041 | 0.524 | 0.44 | 0.03 | 0.006 | 0.689 | 0.07 | 0.18 | 0.061 | |
| Ged | Ge | |||||||||||||
| 20 at% Ged:8 at% Yb:CNGG | 12.8 | 7 | 0.911 | 0.089 | 0.605 | 0.395 | 0.78 | 0.013 | 0.18 | 0.027 | ||||
| Tig | Ti | |||||||||||||
| 10 at% Tie:8 at% Yb:CNGG | 9f | 10 | 0.936 | 0.064 | 0.79 | 0.12 | 0.092 | 0.917 | 0.023 | 0.060 | ||||
In the present study, we grew 20 at% Ge-modified 8 at% Yb:CNGG single crystals. The composition of the powder prepared by SSS was Ca2.76Yb0.24Nb1.0883Ga2.8834Ge0.9833O12, i.e. the incorporation of Ge was equally subtracted from the Nb and Ga compositions to avoid predetermining a specific site occupancy.
3.5.1.a. XAS of Ge in CNGG. A Ca3Ga2Ge3O12 (CGGG) garnet single crystal was also grown via the Czochralski method, as shown in SI Section S4.1, and a powdered CGGG single crystal was used as a reference for the XAS of Ge-modified 8 at% Yb:CNGG, as shown in Fig. 5. Fig. 5a shows similar XANES spectra for both compounds. Fig. 5b shows the Ge K-edge k2·χ(k) weighted EXAFS oscillations, and Fig. 5c shows their Fourier transforms.
The EXAFS standard equation was used for fitting, where the theoretical scattering paths for the garnet-type Ca3Ga2Ge3O12 within the space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d were calculated using the FEFF software.50 EXAFS analyses were performed considering the most relevant single scattering paths to describe the radial distance in the range of 1–4.0 Å. The first shell is comprised of the Ge–O1 tetrahedral site, the second shell has the Ge–Ca scattering path (CN = 2), the third shell is made of Ge–Ga with CN = 4 and the last shell is made of both Ge–Ga and Ge–Ca at a similar distance and with CN = 4. The introduction of the Ge–Ca shell is necessary to reproduce the signal at long distances. Indeed, the removal of the Ge–Ca path gave a negative σ2 value for the Ge–Ga shell, indicating the need for an additional signal. It is important to remember that the assignment of the scatterer, especially in the case of Ga and Ge, was made according to the CIF file of the reference compound because Ge–O and Ge–Ga scatterers cannot be distinguished from EXAFS. The fit of the EXAFS spectra at the Ge K-edge of the CGGG reference shows the local structure of Ge4+ in the garnet, where Ge4+ ions are surrounded by 4 oxygens at 1.77(2) Å, 2 Ca at 3.06(2) Å and 4 Ga, Ge and Ca at 3.44(2), 3.74(2) and 3.78(5) Å, respectively. In the case of the Ge-modified 8 at% Yb:CNGG crystal, its EXAFS signal is similar to that of the CGGG reference and good agreement between the data and fit is obtained considering Ge4+ ions in the tetrahedral 24d sites of the CNGG garnet structure. Table S5 lists the bond distances obtained for the CGGG and Ge-modified 8 at% Yb:CNGG crystals.
d were calculated using the FEFF software.50 EXAFS analyses were performed considering the most relevant single scattering paths to describe the radial distance in the range of 1–4.0 Å. The first shell is comprised of the Ge–O1 tetrahedral site, the second shell has the Ge–Ca scattering path (CN = 2), the third shell is made of Ge–Ga with CN = 4 and the last shell is made of both Ge–Ga and Ge–Ca at a similar distance and with CN = 4. The introduction of the Ge–Ca shell is necessary to reproduce the signal at long distances. Indeed, the removal of the Ge–Ca path gave a negative σ2 value for the Ge–Ga shell, indicating the need for an additional signal. It is important to remember that the assignment of the scatterer, especially in the case of Ga and Ge, was made according to the CIF file of the reference compound because Ge–O and Ge–Ga scatterers cannot be distinguished from EXAFS. The fit of the EXAFS spectra at the Ge K-edge of the CGGG reference shows the local structure of Ge4+ in the garnet, where Ge4+ ions are surrounded by 4 oxygens at 1.77(2) Å, 2 Ca at 3.06(2) Å and 4 Ga, Ge and Ca at 3.44(2), 3.74(2) and 3.78(5) Å, respectively. In the case of the Ge-modified 8 at% Yb:CNGG crystal, its EXAFS signal is similar to that of the CGGG reference and good agreement between the data and fit is obtained considering Ge4+ ions in the tetrahedral 24d sites of the CNGG garnet structure. Table S5 lists the bond distances obtained for the CGGG and Ge-modified 8 at% Yb:CNGG crystals.
3.5.1.b. scXRD of Ge-modified Yb:CNGG. The Ge4+ site position in the CNGG garnet cannot be discerned exclusively from the scXRD data analysis because of the close atomic numbers of Ga (Z = 31) and Ge (Z = 32). However, once the Ge4+ position has been determined based on the XAS analysis as the 24d garnet site, and taking into account the cationic composition results from EPMA, the scXRD structure refinement of the Ge-modified 8 at% Yb:CNGG crystal was carried out. In the final refinement cycles, the procedure considered a fixed Nb5+ 24d occupancy (with a value similar to that obtained for previous CNGG crystals), whereas the Ga3+ and Ge4+ occupancies over the 24d sites were allowed to vary. The obtained 24d Ge4+ occupancy was in accordance with the EPMA analysis, as shown in Table 3 and Table S9. Later, by fixing these Ga3+ and Ge4+ occupancies, the Nb5+ population in the 24d site was refined. The last refinement cycle yielded the lowest discrepancy factor R1 [I > 2σ(I)] = 0.0104. According to this, the number of 24d vacant sites was estimated as ≈3%. Table 2 and Table S8 include these data as well as the unit cell parameter, the oxygen positional coordinates, and Ca2+, Yb3+, Nb5+ and Ga3+ populations over the other available dodecahedral 24c and octahedral 16a garnet sites. Positive values of the anisotropic thermal displacements were obtained for all atoms.
3.5.1.c. OA of Yb3+ in Ge modified 8 at% Yb:CNGG. Fig. 3c shows the OA of the Ge-modified 8 at% Yb:CNGG crystal measured at T = 6 K. Firstly, it is worth noting the strong decrease in intensity of the λ = 973 nm band formerly associated with the presence of a 24d vacancy nearby Yb3+. The main band at λ = 971.1 nm appears broader than in the unmodified 8 at% Yb:CNGG crystal because of the evident presence of a band shoulder at the high-energy band wing. The band spectral decomposition evidences a band contribution at λ = 969.6 nm (10314 cm−1), with the details presented in SI Fig. S14 and Table S10. It is important to note that this new band induced by the presence of Ge4+ appears at a higher energy than that induced by any other studied cations with lower oxidation states in the Yb3+ neighbourhood.
3.5.2.a. XAS of Ti4+ in 8 at% Yb:CNGG. The XANES spectrum of 10 at% Ti-modified 8 at% Yb:CNGG was collected, along with that of other reference oxides with 6-fold (SrTiO3) or 4-fold (Y2TiMoO8 and α′-Ba2TiO4) Ti–O coordinations. SrTiO3 powder was obtained by grinding a bulk single crystal, while α′-Ba2TiO4 and Y2TiMoO8 microcrystals were synthesised following previously described methods,54,55 and SI Sections SI4.2 and S4.3 present the details.
Fig. 6a depicts a comparison of the collected XANES. Previous XAS studies have established that the XANES spectra of 4-fold coordinated Ti is characterized by a well-resolved peak at 4969.8 ± 1.0 eV, which is absent in the XANES spectrum of 6-fold coordinated Ti.56 This XANES peak is clearly observed in Fig. 6a for α′-Ba2TiO4 and Y2TiMoO8, but it is not observed in the 10 at% Ti-modified 8 at% Yb:CNGG crystal; thus, we can confidently conclude that Ti4+ does not occupy the 24d tetrahedral site of the garnet. Given that dodecahedral Ti occupation is not known in garnets, the only remaining possibility for Ti in CNGG is the octahedral 16a site.
Fig. 6b shows the EXAFS spectra of the 10 at% Ti-modified 8 at% Yb:CNGG crystal in comparison to that of the octahedral Ti (CN = 6) in the SrTiO3 perovskite. The fit of the EXAFS spectra at the Ti K-edge of the SrTiO3 reference agrees with the known values for the perovskite with Ti4+ ions surrounded by 6 oxygens at 1.96(2) Å, 8 Sr cations at 3.40(3) Å and 6 Ti cations at 4.00(6) Å. In the case of Ti in the CNGG single crystal, a good fit of the experimental EXAFS data is obtained considering Ti4+ surrounded by 6 oxygens at a distance of 1.96(2) Å, followed by 6 Ca cations at 3.41(4) Å and 6 Ga cations at 3.44(3) Å. These radial distances are evidenced in the EXAFS weighted FT, as shown in Fig. 6c. The comparison of the EXAFS-derived Ti radial bond distances with that expected in the three crystallographic sites of the garnet, as seen in SI Table S2, agrees exclusively for Ti4+ cations occupying the octahedral 16a site of the CNGG garnet lattice.
3.5.2.b. scXRD of Ti-modified 8 at% Yb:CNGG. In the case of CNGG, the radius mismatch for the replacement of Nb5+/Ga3+ with Ti4+ is Δr = −5.47% and Δr = −10.64% for the 16a and 24d sites, respectively; see in SI Table S1. The comparison of the lattice parameters of 10 at% Ti-modified 8 at% Yb:CNGG, a = 12.4720(3) Å, and that of 8 at% Yb:CNGG, a = 12.4728 Å, as shown in SI Table S2, shows that basically there is no change, which suggests the incorporation of Ti in the site with the smallest radius mismatch, i.e. the octahedral 16a site, in accordance with previous XAS results.
The refinement of the scXRD results given in Table 2 provides an occupancy factor of 0.092 of Ti in the 16a site, i.e., titanium is incorporated during crystal growth with a segregation coefficient close to unity. Both the dodecahedral and octahedral sites are totally occupied, but still 6% of the tetrahedral sites are vacant. Although the Ca and Yb populations on the 24c site are not affected by the incorporation of Ti, as shown in Table 3, the relative Nb/Ga distribution over the 16a site favours the incorporation of Nb5+. On the contrary, in the 24d site, in which Ti is absent, Nb5+ is basically displaced by Ga3+, while the population of tetrahedral vacancies (6%) remains close to that found in 8 at% Yb:CNGG, i.e. 7.5%, as shown in Table 3.
3.5.2.c. OA of Ti-modified 8 at% Yb:CNGG. Fig. 3d shows a comparison of the 0 → 0′ OA of Yb3+ measured at T = 6 K in 10 at% Ti-modified 8 at% Yb:CNGG and in 8 at% Yb:CNGG single crystals. For ease of comparison, both spectra have been normalised to a unit area. It is evident that both spectra are equal, and in particular the optical absorption band at λ = 973 nm is observed in both cases with rather similar intensity as expected due to the slight change in the 24d vacancy density determined based on the scXRD and PALS (Table 1) results. New Yb3+ OA bands are not observed but the increase in the intensity of the λ = 971.1 nm band is consistent with the enhancement in the Ga3+ OF in the 24d site. One can conclude that the modification of the cationic charge over the 16a garnet site (Ga3+/Nb5+ substitution by Ti4+) has no, or very little, influence on the CF on Yb3+.
3.6. Q = 5+: Nb5+ in Yb:CNGG
Nb5+ is a constituent element of the CNGG crystals, which in undoped CNGG is distributed in the 16a and 24d sites in the ratio of 0.86/0.14. Yb3+ doping with high concentrations (>5 at%) displaces this ratio basically to confine all Nb5+ in the 16a octahedral site, and in parallel the concentration of 24c dodecahedral vacancies decreases near zero, while that of the 24d tetrahedral ones remains constant in the OF ≈ 0.075 level, as shown in Table 3.The 6 K OA spectrum of Yb3+ changes very little with an increase in Yb concentration, suggesting that the minor amount of Nb5+ in the tetrahedral 24d site has a minimal contribution to the Yb3+ band shape. Basically, no tetrahedral Nb5+ is found in the 8 at% Yb-doped CNGG crystals, and both the amount of tetrahedral vacancies and the intensity of the λ = 973 nm OA band remain independent of the Yb concentration.
Attempts to dope the CNGG crystals with V5+ as an alternative pentavalent cation failed due to the lack of incorporation of this ion into the garnet lattice, as shown in SI Fig. S7f, and correspondingly no difference in the cryogenic (T = 6 K) OA of Yb3+ was found between the nominally V-modified and non-modified 8 at% Yb:CNGG crystals, as shown in SI Fig. S17.
3.7. Room temperature fluorescence
Fig. 7 shows the Yb3+ luminescence of the Li-, 30 at% Mg- and 10 at% Ge-modified 8 at% Yb:CNGG single crystals. The purpose of this characterization is to determine if the decrease in the tetrahedral cationic vacancies has any effect on the observed bandwidth. For this purpose, plate samples with the same thickness (≈0.2 mm) were tested under identical experimental conditions, i.e. keeping the same excitation power level (130 mW) and wavelength conditions (λEXC = 971.6 nm), as well as monochromator slits (0.2 mm).Fig. 7a and 7b show that the Li- and 30 at% Mg-modified 8 at% Yb:CNGG single crystals have slightly narrower Yb emission than the unmodified 8 at% Yb:CNGG crystal, respectively. On the contrary, in the 10 at% Ge-modified 8 at% Yb:CNGG crystal, the intensity of the Yb3+ emission is observed to increase in the low-energy band side in comparison to the unmodified 8 at% Yb:CNGG crystal.
4. Discussion
The heterovalent substitutional strategy used in the present work pursues the replacement of the 5+ and 3+ electric charges of the constituent Nb and Ga elements with other electric charges in the range of 1+ to 5+. For this purpose, the growth of CNGG single crystals modified with Li+, Mg2+, Si4+, Ge4+, Ti4+, and V5+ cations was attempted. Only Li+, Mg2+, Ge4+, and Ti4+ produced single crystals of the garnet phase. The other cations either do not incorporate into the crystal, as in the case of V5+, or the polycrystalline precursor and solidified materials are not exclusively the garnet phase, as in the case of Si4+. Nonetheless, the range of electric charges, namely, from 0 to 4+, that we are presenting for the successfully grown CNGG single crystals allows us to disclose their influence on the optical properties of Yb3+.Firstly, it must be noted that the CNGG composition is sensitive to the growth conditions as well as to the presence of lanthanide doping elements. In particular, the incorporation of Yb not only reduces the cell volume but also has a deep influence on the density of cationic vacancies and the incorporation of Nb into the tetrahedral 24d site.10,11 Therefore, any comparison of the changes induced by the incorporation of other modifier cations in Yb-doped crystals must employ the proper Yb:CNGG composition as the reference rather than the undoped CNGG single crystal. To compare the different modified Yb:CNGG crystals, we selected a nominal (melt) 8 at% Yb composition in the dodecahedral 24c site for all the presented crystals. However, the segregation coefficient of Yb is also sensitive to other co-dopants and may change from 0.9 to 1.1,13 which should be considered to explain minor fluctuations in the observed results.
Further, the Ga volatility from the melt during the Czochralski growth, which is also observed in other Ga-based crystals,57,58 leads to a small depletion of the Ga/Nb ratio as the crystal is pulled out from the melt during the growth process, as shown in SI Fig. S12a. Given that the crystal becomes enriched in Nb5+ ions, an increase in cationic vacancy density can be expected to maintain charge neutrality, which could explain the increase in the relative intensity of the 6 K 0 → 0′ Yb3+ OA band at λ = 973 nm observed from the seed to the end of the crystal, as shown in SI Fig. S13.
From the point of view of cationic incorporation into the CNGG lattice, the simplest cases to be considered are Ge4+ and Ti4+. The similarity of the XAS results of Ge-modified 8 at% Yb:CNGG and the reference Ca3Ga2Ge3O12 crystal, as shown in Fig. 5, indicates unequivocally that Ge in CNGG sits exclusively in the 24d tetrahedral garnet site (as in the reference). Alternatively, the absence of a peak at 4969.8 eV in the XANES spectrum of the Ti-modified 8 at% Yb:CNGG crystal, as shown in Fig. 6a, rules out its presence in the tetrahedral garnet site, and the similarity of the XANES and EXAFS spectra for the Ti-modified 8 at% Yb:CNGG and SrTiO3 clearly indicates that Ti4+ sits exclusively in the octahedral 16a garnet site. Thus, Ge4+ and Ti4+ are each in a different site of the garnet lattice, and their influence on the Yb3+ 0 → 0′ OA observed at T = 6 K is quite different. Although Ge4+ induces a reduction in the intensity of the λ = 973 nm OA band and creates a new one at λ = 969.9 nm, as shown in Fig. 3c, the presence of Ti4+ does not introduce a significant change in the energy position of the Yb3+ 0 → 0′ OA, as shown in Fig. 3d. Therefore, it can be concluded that the most important contribution to the CF on Yb3+ comes from the occupancy of the 24d tetrahedral sites at the shortest distances to Yb3+ in the 24c sites, as shown in SI Fig. S1 and Table S3. In fact, there are two edge-sharing 24d tetrahedra linked to the 24c dodecahedral polyhedron at the shortest intercationic distance of 3.1242 Å, which are expected to create the strongest CF interaction with Yb3+.
Li is another cation in CNGG that sits exclusively in the tetrahedral 24d garnet site.11 The CLNGG single crystals were grown from a melt composition much closer to the stoichiometric garnet formula than CNGG, i.e. the amount of nominal cationic vacancies in the precursor CLNGG composition is five-times smaller (x = 0.025) than in the CNGG precursor (x = 0.125). The reduction in the cationic vacancy density in CLNGG with regard to CNGG was previously determined by scXRD refinements,11 and now it is experimentally demonstrated by the PALS results presented in Section 3.1.1. Table 1 shows that the intensity of the long-lived lifetime for positron annihilation in the cationic vacancies is reduced by ≈16.6% from CNGG to CLNGG, and by 6.2% from 8 at% Yb:CNGG to 8 at% Yb:CLNGG. On the contrary, in the case of Ti-modified 8 at% Yb:CNGG, the difference with regard to the unmodified 8 at% Yb:CNGG is less than 1%. Clearly, the incorporation of Li reduces the vacancy density upon the site it enters, i.e. the tetrahedral 24d garnet site. In parallel to this cationic vacancy reduction, Fig. 3a shows a decrease in the intensity of the λ = 973 nm Yb3+ OA band observed at T = 6 K upon the incorporation of Li+. Thus, in parallel to the previous discussion for Ge4+, this decrease in the Yb3+ OA must be ascribed to the reduction in vacant tetrahedral sites in the first neighbor cationic shell around the dodecahedral Yb3+. Further, the OA intensity loss at λ = 973 nm is parallel to the appearance of a new band at 971.9 nm in 8 at% Yb:CLNGG.
A decrease in the λ = 973 nm band intensity and the appearance of a new Yb3+ OA band at λ = 971.3 nm are also observed for the 30 at% Mg-modified 8 at% Yb:CNGG single crystal. In this case, the reduction in the λ = 973 nm band intensity is clear but its amount is smaller than that for the Li+ or Ge4+ cases. Unlike the incorporation of Li+, Ti4+ or Ge4+, the Mg2+ in 8 at% Yb:CNGG crystal is not located at a single site. The Mg-modified Yb:CNGG XANES spectrum in Fig. 4a shows features corresponding to the three garnet sites, and the scXRD refinement quantified this distribution as 17% (24c), 8% (16a) and 75% (24d) of the total Mg composition. The PALS results elucidate that the vacancy density in the Mg-modified 8 at% Yb:CNGG is intermediate between that of 8 at% Yb:CNGG and 8 at% Yb:CLNGG; thus, one would expect a lower reduction in the λ = 973 nm OA band intensity than in the Li and Ge cases. In fact, this is observed in the comparison of Fig. 3a and c with 3b. Thus, the presence of Mg2+ in the 24d tetrahedral site induces similar spectroscopic changes in the Yb 0 → 0′ OA than that observed for other heterovalent cations in this same site, while the Mg fraction in the dodecahedral and octahedral sites would behave as the Ti4+ case, i.e. they do not have much influence on the Yb3+ energy level position.
Ga3+ is the most abundant cation on the 24d tetrahedral site (OF ≈ 0.8). It even displaces 24d Nb5+ to compensate for the increase in electric charge associated with Yb3+ doping in the Ca2+ site, reaching OF > 0.9. The most intense Yb 0 → 0′ band at λ = 971.1 nm must be associated with the most abundant environment around Yb, i.e., where all the tetrahedral and octahedral first neighbors are occupied by 24d Ga3+ and 16a Nb5+, respectively.
In summary, we have shown that the different Yb3+ 0 → 0′ OA bands observed at λ = 973 nm, 971.9 nm, 971.3 nm, 971.1 nm and 969.6 nm can be correlated with the presence of a vacancy (Q = 0), Li+ (Q = 1), Mg2+ (Q = 2), Ga3+ (Q = 3) and Ge4+ (Q = 4) in the tetrahedral garnet site, respectively, while the presence of Ti4+ in the octahedral site substituting Nb5+ has no observable effect on the energy position of Yb3+ OA. This shows that the main contribution to the CF on the Yb3+ sites arises from the electric charges at the closest tetrahedra.
Nb5+ is indeed found in the tetrahedral sites of CNCG. According to the findings described above, it could be expected that it would contribute with a Yb3+ 0 → 0′ OA band at λ < 969.6 nm. However, the Nb 24d OF is only 10%, and as already mentioned, the presence of Yb3+ decreases the Nb 24d OF to 0.5–0.3%. It seems likely that such a minor amount of Nb5+ in the tetrahedral site cannot be resolved in the experimental spectra despite the high spectral resolution used.
From a mode-locked lasing point of view, the interest is to find how the changes introduced in the energy of the Yb3+ electronic levels may modify the fluorescence bandwidth. Fig. 7a and b show that in parallel with the disappearance of the λ = 973 nm 0 → 0′ OA band, the Yb3+ fluorescence becomes slightly narrower. This is consistent with the reduction in the range of energies exhibited by the available Yb centres in each case including 1.2744–1.2769 eV (λ = 973–971.1 nm) for Yb:CNGG versus 1.2758–1.2769 eV (λ = 971.9–971.1 nm) in the Yb:CLNGG case. Thus, elimination of the tetrahedral vacancies present in CNGG would not be desirable for a reduction in the laser pulse duration. However, Fig. 7c shows that in the 20 at% Ge-modified 8 at% Yb:CNGG case, some band broadening is observed despite the fact that Ge in the tetrahedral 24d garnet site also reduces the concentration of cationic vacancies of this site. Somehow, the new OA observed at λ = 969.9 nm associated with the presence of a 4+ charge in the 24d site is able to compensate for the loss of centres with absorption at λ = 973 nm. Nevertheless, this preliminary conclusion must be taken with caution because the actual Yb concentration in the crystals is reduced from 9.1 at% in nominally 8 at% Yb:CNGG to 7–7.5 at% in the Li- or Mg-modified 8 at% Yb:CNGG crystals; on the contrary, in the case of the used Ge-modified crystal, the Yb concentration increases up to 12.8 at%. These modifications in the Yb concentration may have an influence in the Yb3+ fluorescence profile due to the emission reabsorption. Future work is required to confirm the Yb3+ fluorescence profiles free of fluorescence reabsorption as well as to extend these concepts to the most common 3–5 at% Yb concentration level used in laser applications.
Several works, some of them described in the Introduction, have studied isovalent substitutions in YAG single crystals or transparent ceramics59 to modify the Yb3+ electronic level energies but without great success. Heterovalent substitutions in YAG have been rarely attempted. One such case was the mixing of Yb:YAG with Mn3Al2(SiO4)3 garnets.60 In the latter work, the heterovalent substitutions of Y3+ by Mn2+ and Al3+ by Si4+ were attempted. Unfortunately, the incorporation of Si into the crystal was not detected, as in the current case of Si-modified CNGG, as shown in SI Sections S2.2 and S8.2; thus, no modification of the tetrahedral garnet site was achieved. Conversely, Mn2+ sits in the dodecahedral site, or it could also be distributed in the octahedral site; see in SI Fig. S1. However, as discussed above, the electric charge modification on these sites has little influence on the Yb3+ 0 → 0′ OA. As a result, the Yb3+ fluorescence bandwidth obtained through this YAG modification was only FWHM = 140 cm−1, which is somehow higher than in Yb:YAG (FWHM = 85 cm−1), but far below that observed in Yb:CNGG (FWHM = 220 cm−1). From this perspective, the heterovalent substitution of Al3+ with Ge4+, rather than Si4+, would seem more favourable, although in the ceramic processing, other factors, such as refractive index matching, could limit the transparency.
5. Conclusions
Single crystal growth of 8 at% Yb-doped Ca3(NbGa□)5O12-type garnet (CNGG) modified with other optically silent cations was possible for Li+, Mg2+, Ge4+ and Ti4+ within some incorporation limits of ≈10% of the corresponding site occupancy. These heterovalent substitutions of the trivalent (Ga3+) and pentavalent (Nb5+) constituent cations simultaneously introduce some lattice strain and electric charge misfit in the CNGG crystalline lattice. The 2F7/2(0) → 2F5/2(0′) transition (shortly 0 → 0′) of Yb3+ measured at T = 6 K has been found to be a sensitive local probe for the crystal field (CF) changes introduced by these crystal modifications.The combined X-ray absorption (XAS) and single crystal diffraction (scXRD) analyses of Mg-, Ge- and Ti-modified Yb:CNGG single crystals, along with previous studies on the Li case, show that Li and Ge are found exclusively in the tetrahedral 24d crystal garnet site and Ti is found exclusively in the octahedral 16a site, while Mg distributes in the three (dodecahedral, 24c; octahedral, 16a; and tetrahedral 24d) garnet sites.
Previous scXRD studies showed that cationic vacancies in the three crystal sites are characteristic of undoped CNGG, but in CNGG crystals doped with Yb in excess of 5 at%, they are found with significance only in the tetrahedral 24d site. This view is now corroborated by positron annihilation lifetime spectroscopy (PALS), which shows a significant reduction in the intensity of the long-lived lifetime characteristic of positron annihilation at the vacancy defects upon Yb doping. The PALS results show a further reduction in the Yb:CNGG vacancy density when the crystal incorporates Li (as anticipated by scXRD in previous works), and to a lesser extent, Mg, but Ti incorporated in the octahedral 16a site does not reduce the concentration of cationic vacancies present in Yb:CNGG.
The 0 → 0′ Yb3+ optical absorption (OA) shows several bands related to the coexistence of several Yb3+ centres in the disordered CNGG host. The most intense OA band of Yb:CNGG at λ = 971.1 nm should be related to the most common Yb environment associated with the exclusive presence of Ga3+ in the nearest-to-Yb 24d tetrahedral site. Another less intense but well-resolved OA band at λ = 973 nm is also found in the non-modified Yb:CNGG crystals. The intensity of the latter band increases as the crystal growth proceeds, i.e. its intensity is larger at the crystal end than at the beginning, which is associated with a decrease in Ga incorporation as the growth proceeds. This minor band at λ = 973 nm is ascribed to the presence of an empty tetrahedral vacancy with zero electric charge nearby Yb3+.
Heterovalent cations incorporated in the tetrahedral site, such as Li+, Mg2+ and Ge4+, simultaneously reduce the cationic vacancy density on this site and the intensity of the λ = 973 nm Yb3+ OA. Conversely, the incorporation of Ti4+ in the octahedral site does not modify the OA Yb3+ spectra. The modification of the Yb3+ environment produces new OA bands at λ = 971.9 nm for Li+, λ = 971.3 nm for Mg2+, and λ = 969.6 nm for Ge4+. Consequently, the position of the 0 → 0′ Yb3+ OA shifts to a higher energy (shorter wavelength) as the cationic electric charge in the Yb3+ neighbourhood increases. This shows that heterovalent substitution in the tetrahedral 24d site of the garnet structure is the main driving force to change the CF on Yb and could be implemented in laser garnets (YAG and others) either by crystal growth or ceramic processing with the potential of larger inhomogeneous fluorescence broadening than that in the previously widely conducted isovalent substitution strategy.
Author contributions
All authors contributed to conceptualization, investigation, data analysis and funding acquisition. The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this study have been included within the article and the corresponding supplementary information (SI) and CIF materials. Further data are available from the corresponding author upon reasonable request.Supplementary information about garnet crystallography, growth of modified-Yb:CNGG and XAS reference single crystals, EXAFS and XRD analyses, as well as further optical spectroscopic characterizations, is available. See DOI: https://doi.org/10.1039/d5tc03824c.
CCDC 2448685, 2448696 and 2448697 contain the supplementary crystallographic data for this paper.61a–c
Acknowledgements
This work has been supported by grants PDC2022-133326-I00 (funded by MICIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR), PID2021-128090OB-C21 (funded by MICIN/AEI/10.13039/501100011033 and by “ERFD A way of making Europe”), CEX2024-001445-S Severo Ochoa Centres of Excellence grant, and partially by JSPS via Grant-in-Aid for Transformative Research Areas (A) “Hyper-ordered Structure Science” (no. 23H04094, 23H04119, and 20H05882). Mg and Ti XAS results were performed at SOLEIL under proposal 20210943, and Prof. P. Lagarde is acknowledged for helping with XAS data acquisition. Ge XAS results were performed at the CELLS-ALBA facility under proposal 2023097812. EPMA analyses have been performed by A. Fernández Larios at the Centro Nacional de Microscopía Electrónica of Universidad Complutense de Madrid. The contributions of J. Perles and M. Ramírez (SIdI-Universidad Autónoma de Madrid) to the scXRD measurements are also acknowledged.References
- U. Keller, Ultrafast Lasers. A comprehensive introduction to fundamental principles with practical applications, Springer, Switzerland AG, 2021, ch. 2. DOI:10.1007/978-3-030-82532-4, ISBN 978-3-030-82531-7.
- C. Hönninger, R. Paschotta, M. Graf, F. Morier-Genoud, G. Zhang, M. Moser, S. Biswal, J. Nees, A. Braun, G. A. Mourou, I. Johannsen, A. Giesen, W. Seeber and U. Keller, Ultrafast ytterbium-doped bulk lasers and laser amplifiers, Appl. Phys. B, 1999, 69, 3–17, DOI:10.1007/s003400050762.
- J. Drs, J. Fischer, N. Modsching, F. Labaye, V. J. Wittwer and T. Sudmeyer, Sub-30-fs Yb:YAG thin-disk laser oscillator operating in the strongly self-phase modulation broadened regime, Opt. Express, 2021, 29, 35929, DOI:10.1364/OE.440196.
- J. Dong, K. Ueda and A. A. Kaminskii, Continuous-wave and Q-switched microchip laser performance of Yb:Y3Sc2Al3O12 crystals, Opt. Express, 2008, 16(8), 5241–5251, DOI:10.1364/OE.16.005241.
- J. Koerner, C. Vorholt, H. Liebetrau, M. Kahle, D. Kloepfel, R. Seifert, J. Hein and M. C. Kaluza, Measurement of temperature-dependent absorption and emission spectra of Yb:YAG, Yb:LuAG, and Yb:CaF2 between 20 °C and 200 °C and predictions on their influence on laser performance, J. Opt. Soc. Am. B, 2012, 29(9), 2493–2502, DOI:10.1364/JOSAB.29.002493.
- H. Yu, K. Wu, B. Yao, H. Zhang, Z. Wang, J. Wang, Y. Zhang, Z. Wei, Z. Zhang, X. Zhong and M. Jiang, Growth and characteristics of Yb-doped Y3Ga5012 laser crystal, IEEE J. Quantum. Electron., 2010, 46(12), 1689–1695, DOI:10.1109/JQE.2010.2059373.
- M. O. Ramírez, L. E. Bausá, E. Cavallia and E. Bovero, Optical spectroscopy of Yb3+-doped Ca3Sc2Ge3O12 garnet crystal, J. Appl. Phys., 2006, 99, 013507, DOI:10.1063/1.2150261.
- J. O. Álvarez-Pérez, J. M. Cano-Torres, A. Ruiz, M. D. Serrano, C. Cascales and C. Zaldo, Correction: A roadmap for laser optimization of Yb:Ca3(NbGa)5O12-CNGG-type single crystal garnets, J. Mater. Chem. C, 2021, 9, 6945–6946, 10.1039/d1tc90105b.
- V. Lupei, A. Lupei, C. Gheorghe, L. Gheorghe, A. Achim and A. Ikesue, Crystal field disorder effects in the optical spectra of Nd3+ and Yb3+-doped calcium lithium niobium gallium garnets laser crystals and ceramics, J. Appl. Phys., 2012, 112, 063110, DOI:10.1063/1.4752070.
- E. Castellano-Hernández, M. D. Serrano, R. J. Jiménez-Riobóo, C. Cascales, C. Zaldo, A. Jezowski and P. A. Loiko, Na modification of lanthanide doped Ca3Nb1.5Ga3.5O12-type laser garnets: Czochralski crystal growth and characterization, Cryst. Growth Des., 2016, 16, 1480–1491, DOI:10.1021/acs.cgd.5b01607.
- M. D. Serrano, J. O. Álvarez-Pérez, C. Zaldo, J. Sanz, I. Sobrados, J. A. Alonso, C. Cascales, M. T. Fernández-Díaz and A. Jezowski, Design of Yb3+ optical bandwidths by crystallographic modification of disordered calcium niobium gallium laser garnets, J. Mater. Chem. C, 2017, 5, 11481, 10.1039/C7TC02760E.
- C. Gheorghe, S. Hau, L. Gheorghe, F. Voicu, M. Greculeasa, A. Broasca and G. Stanciu, RE3+-doped Ca3(Nb,Ga)5O12 and Ca3(Li,Nb,Ga)5O12 crystals (RE = Sm, Dy, and Pr): A review of current achievements, Materials, 2023, 16, 269, DOI:10.3390/ma16010269.
- J. O. Álvarez-Pérez, J. M. Cano-Torres, A. Ruiz, M. D. Serrano, C. Cascales and C. Zaldo, A roadmap for laser optimization of Yb:Ca3(NbGa)5O12-CNGG-type single crystal garnet, J. Mater. Chem. C, 2021, 9, 4628–4642, 10.1039/D0TC05718E.
- J. I. Goldstein, D. E. Newbury, P. Echlin, D. C. Joy, A. Roming, C. Lyman, C. Fiori and E. Lifshin, Scanning Electron Microscopy and X-ray Microanalysis, Plenum, New York, 1992 Search PubMed.
- M. Yamawaki, Y. Kobayashi, K. Hattori and Y. Watanabe, Novel system for potential nondestructive material inspection using positron annihilation lifetime spectroscopy, Jpn. J. Appl. Phys., 2011, 50, 086301, DOI:10.1143/JJAP.50.086301.
- J. Kansy and D. Giebel, Study of defect structure with new software for numerical analysis of PAL spectra, J. Phys: Conf. Ser., 2011, 265, 012030, DOI:10.1088/1742-6596/265/1/012030.
- R. Kraus-Rehberg and H. S. Leipner, Positron Annihilation in Semiconductor: Defect Studies, Springer-Verlag, Berlin/Heidelberg, 1st edn, 2010, p. 13 Search PubMed.
- M. Kitaura, Y. Taira and S. Watanabe, Characterization of imperfections in scintillator crystals using gamma-ray induced positron annihilation lifetime spectroscopy, Opt. Mater: X, 2022, 14, 100156, DOI:10.1016/j.omx.2022.100156.
- D. Vantelon, N. Trcera, D. Roy, T. Moreno, D. Mailly, S. Guilet, E. Metchalkov, F. Delmotte, B. Lassalle, P. Lagarde and A. M. Flank, The LUCIA beamline at SOLEIL, J. Synchrotron Radiat., 2016, 23, 635–640, DOI:10.1107/S1600577516000746.
- L. Simonelli, C. Marini, W. Olszewski, M. Ávila Pérez, N. Ramanan, G. Guilera, V. Cuartero and K. Klementiev, CLAESS: The hard X-ray absorption beamline of the ALBA CELLS Synchrotron, Cogent Phys., 2016, 3(1), 1–10, DOI:10.1080/23311940.2016.1231987.
- B. Ravel and M. Newville, ATHENA, ARTEMIS, HEPHAESTUS: Data Analysis for X-Ray Absorption Spectroscopy Using IFEFFIT, J. Synchrotron Radiat., 2005, 12(4), 537–541, DOI:10.1107/S0909049505012719.
- SHELXTL (V 6.10) Software Package, Siemens Energy and Automation Inc. Analytical Instrumentation.
- K. Shimamura, M. Timoshechkin, T. Sasaki, K. Hoshikawa and T. Fukuda, Growth and characterization of calcium niobium gallium garnet (CNGG) single-crystals for laser applications, J. Cryst. Growth, 1993, 128(1–4), 1021–1024, DOI:10.1016/S0022-0248(07)80090-X.
- Yu. K. Voronko, A. A. Sobol, A. Ya Karasik, N. A. Eskov, P. A. Rabochkina and S. N. Ushakov, Calcium niobium gallium and calcium lithium niobium gallium garnets doped with rare earth ions-effective laser media, Opt. Mater., 2002, 20, 197–209, DOI:10.1016/S0925-3467(02)00063-0.
- A. A. Kaminskii, E. L. Belokoneva, A. V. Butashin, K. Kurbanov, A. A. Markosyan, B. V. Mill, O. K. Nikol’skaya and S. É. Sarkisov, Crystal structure and spectral luminescence properties of the cation-deficient garnet Ca3(Nb,Ga)2Ga3O12-Nd, Inorg. Mater., 1986, 22(7), 927–936 Search PubMed.
- Y. Ono, K. Shimamura, Y. Morii, T. Fukuda and T. Kajinati, Structure analysis of a Ca–Nb–Ga garnet, Phys. B, 1995, 213, 420–422, DOI:10.1016/0921-4526(95)00176-A.
- F. A. Selim, C. R. Varney, M. C. Tarun, M. C. Rowe, G. S. Collins and M. D. McCluskey, Positron lifetime measurements of hydrogen passivation of cation vacancies in yttrium aluminum oxide garnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 174102, DOI:10.1103/PhysRevB.88.174102.
- K. Fujimori, M. Kitaura, Y. Taira, M. Fujimoto, H. Zen, S. Watanabe, K. Kamada, Y. Okano, M. Katoh, M. Hosaka, J. Yamazaki, T. Hirade, Y. Kobayashi and A. Ohnishi, Visualizing cation vacancies in Ce:Gd3Al2Ga3O12 scintillators by gamma-ray-induced positron annihilation lifetime spectroscopy, Appl. Phys. Express, 2020, 13, 085505, DOI:10.35848/1882-0786/aba0dd.
- J. Dong and K. Lu, Noncubic symmetry in garnet structures studied using extended X-ray-absorption fine-structure spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 8808, DOI:10.1103/PhysRevB.43.8808.
- J. O. Álvarez-Pérez, J. M. Cano-Torres, M. D. Serrano, C. Cascales and C. Zaldo, A probe of the radiation field magnetic component based on octahedral Yb3+ in the CaNbGa garnet -CNGG- single crystal, J. Mater. Chem. C, 2020, 8, 7882–7889, 10.1039/d0tc01608j.
- R. Pappalardo and D. L. Wood, Spectrum of Yb3+ in yttrium gallium garnet, J. Chem. Phys., 1960, 33, 1734–1742, DOI:10.1063/1.1731494.
- S. Geller, Crystal chemistry of the garnets, Z. Kristallogr., 1967, 125, 1–47, DOI:10.1524/zkri.1967.125.16.1.
- J. Song, K. Song, J. Wei, H. Lin, J. Wu, J. Xu, W. Su and Z. Cheng, Ionic occupation, structures, and microwave dielectric properties of Y3MgAl3SiO12 garnet-type ceramics, J. Am. Ceram. Soc., 2017, 101, 244–251, DOI:10.1111/jace.15174.
- N. Trcera, D. Cabaret, S. Rossano, F. Farges, A. Flank and P. Lagarde, Experimental and theoretical study of the structural environment of magnesium in minerals and silicate glasses using X-ray absorption near-edge structure, Phys. Chem. Miner., 2009, 36, 241–257, DOI:10.1007/s00269-008-0273-z.
- P. Ildefonse P, G. Calas, A. M. Flank and P. Lagarde, Low Z elements (Mg, Al, and Si) K-edge X-ray absorption spectroscopy in minerals and disordered systems, Nucl. Instrum. Methods Phys. Res., Sect. B, 1995, 97, 172–175, DOI:10.1016/0168-583X(94)00710-1.
- D. Li, M. Peng and T. Murata, Coordination and local structure of magnesium in silicate minerals and glasses: Mg K-edge XANES study, Can. Mineral., 1999, 37, 199–206 Search PubMed.
- G. Sankar, D. Gleeson, C. R. A. Catlow, J. M. Thomas and A. D. Smith, The architecture of Mg(II) centres in MAPO-36 solid acid catalysts, J. Synchrotron Radiat., 2001, 8, 625–627, DOI:10.1107/S0909049501000139.
- H. Yang, R. Hazen and R. Downs, et al., Structural change associated with the incommensurate-normal phase transition in akermanite, Ca2MgSi2O7, at high pressure, Phys. Chem. Miner., 1997, 24, 510–519, DOI:10.1007/s002690050066.
- H. Mohammadi, R. M. Da Silva, A. Zeidler, L. V. D. Gammond, F. Gehlhaar and M. Jr. de Oliveira, et al., Structure of diopside, enstatite, and magnesium aluminosilicate glasses: a joint approach using neutron and X-ray diffraction and solid-state NMR, J. Chem. Phys., 2022, 157(21), 214503, DOI:10.1063/5.0125879.
- C. Téqui, R. A. Robie, B. S. Hemingway, D. R. Neuville and P. Richet, Melting and thermodynamic properties of pyrope (Mg3Al2Si3012), Geochim. Cosmochim. Acta, 1991, 55, 1005–1010, DOI:10.1016/0016-7037(91)90158-2.
- J. Zhang and C. Herzberg, Melting of pyrope, Mg3Al2Si4O12, at 7-16 GPa, Am. Mineral., 1994, 79, 497–503 Search PubMed.
- B. V. Mills, Crystallisation of germanium and silicate garnets from solutions in molten salts, Sov. Phys. Crystallogr., 1975, 19(5), 653–655 Search PubMed.
- A. Agnesi, S. DellAcqua, A. Guandalini, G. Reali, A. Toncelli, M. Tonelli and E. Cavalli, Laser action in cw diode-pumped Nd:Ca3Sc2Ge3O12 crystal, Appl. Phys. B, 2000, 71, 153–156, DOI:10.1007/s003400000277.
- J. P. M. Damen, J. A. Pistorious and J. M. Robertson, Calcium gallium germanium garnet as a substrate for magnetic bubble application, Mater. Res. Bull., 1977, 12, 73–78, DOI:10.1016/0025-5408(77)90090-3.
- E. J. Sharp, J. E. Miller, D. J. Horowitz, A. Linz and V. Belruss, Optical spectra and laser action in Nd3+ doped CaY2Mg2Ge3O12, J. Appl. Phys., 1974, 45, 4974–4979, DOI:10.1063/1.1663166.
- A. A. Setlur, W. J. Heward, Y. Gao, A. M. Srivastava, R. G. Chandran and M. V. Shankar, Crystal chemistry and luminescence of Ce3+-doped Lu2CaMg2(Si,Ge)3O12 and its use in LED based lighting, Chem. Mater., 2006, 18, 3314–3322, DOI:10.1021/cm060898c.
- H. Mei, L. Zhang, C. Li, Z. Rao and L. Shu, Compositional design stability, and microwave dielectric properties in Ca3MgBGe3O12 (B = Zr, Sn) garnet ceramics with tetravalent cations on B-site, Ceram. Int., 2022, 48, 4658–4664, DOI:10.1016/j.ceramint.2021.11.001.
- J. Chen, H. Yan, A. Kuwabara, M. D. Smith, Y. Iwasa, H. Ogino, Y. Matsushita, Y. Tsujimoto, K. Yamaura and H. zur Loye, Flux crystal growth, crystal structure, and optical properties of new germanate garnet Ce2CaMg2Ge3O12, Front. Chem., 2020, 8, 91, DOI:10.3389/fchem.2020.00091.
- J. E. Miller, E. J. Sharp and D. J. Horowitz, Optical spectra and laser action of Neodymium in a crystal Ba0.25Mg2.75Y2Ge3O12, J. Appl. Phys., 1972, 43, 462–465, DOI:10.1063/1.1661140.
- J. J. Kas, F. D. Vila and J. J. Rehr, The FEFF Code, Wiley Online Library, Chester, UK, 2020, pp. 1–6; ISBN 9781119433941 Search PubMed.
- M. R. Ackerson, N. D. Tailby and E. B. Watson, XAFS spectroscopic study of Ti coordination in garnet, Am. Mineral., 2017, 102, 173–183, DOI:10.2138/am-2017-5633.
- V. Cantavella, J. Carda, G. Monros, M. A. Tena, P. Escribano and J. Alarcon, Zr4+ and Ti4+ substitution in gallium garnets, J. Mater. Chem., 1993, 3(10), 1059–1064, 10.1039/JM9930301059.
- H. Yamane and T. Kawano, Preparation, crystal structure and photoluminescence of garnet-type calcium tin titanium aluminates, J. Solid State Chem., 2011, 184, 965–970, DOI:10.1016/j.jssc.2011.02.016.
- J. A. Bland, The crystal structure of barium orthotitanate, Ba2TiO4, Acta Crystallogr., 1961, 14, 875, DOI:10.1107/S0365110X61002527.
- J. R. Günter and G. B. Jameson, Orthorhombic barium orthotitanate, α′-Ba2TiO4, Acta Crystallogr., 1984, C40, 207–210, DOI:10.1107/S0108270184003619.
- F. Farges, G. E. Brown Jr and J. J. Rehr, Coordination chemistry of Ti(IV) in silicate glasses and melts: I. XAFS study of titanium coordination in oxide model compounds, Geochim. Cosmochim. Acta, 1996, 60(16), 3023–3038, DOI:10.1016/0016-7037(96)00144-5.
- Z. Galazka, R. Uecker, K. Irmscher, M. Albrecht, D. Klimm, M. Pietsch, M. Brützam, R. Bertram, S. Ganschow and R. Fornari, Czochralski growth and characterization of β-Ga2O3 single crystals, Cryst. Res. Technol., 2010, 45, 1229, DOI:10.1002/crat.201000341.
- V. Kochurikhin, K. Kamada, K. J. Kim, M. Ivanov, L. Gushchina, Y. Shoji, M. Yoshino and A. Yoshikawa, Czochralski growth of 4-inch diameter Ce:Gd3Al2Ga3O12 single crystals for scintillator applications, J. Cryst. Growth, 2020, 531, 125384, DOI:10.1016/j.jcrysgro.2019.125384.
- A. Ikesue and Y. L. Aung, Synthesis and performance of advanced ceramic lasers, J. Am. Ceram. Soc., 2006, 89(6), 1936–1944, DOI:10.1111/j.1551-2916.2006.01043.x.
- Q. Wei, S. Sun, F. Yuan, Y. Huang, L. Zhang, W. Chen and Z. Lin, A novel solid-solution garnet Yb:YAG-MnASG with enhanced spectral properties, J. Alloys Compd., 2019, 786, 77e83, DOI:10.1016/j.jallcom.2019.01.308.
- (a) CCDC 2448685: Experimental Crystal Structure Determination, 2025 DOI:10.25505/fiz.icsd.cc2n61vs; (b) CCDC 2448696: Experimental Crystal Structure Determination, 2025 DOI:10.25505/fiz.icsd.cc2n6265; (c) CCDC 2448697: Experimental Crystal Structure Determination, 2025 DOI:10.25505/fiz.icsd.cc2n6276.
| This journal is © The Royal Society of Chemistry 2026 |






