 Open Access Article
Open Access ArticleDisclosing the molecular structure and dynamics of naphthalene diimide based organic semiconductors in the solid state
Marco
Severi
 *a,
Simiao
Yu
b,
Isaac
Abrahams
*a,
Simiao
Yu
b,
Isaac
Abrahams
 b,
Christian B.
Nielsen
b,
Christian B.
Nielsen
 *b and
Daniele
Fazzi
*b and
Daniele
Fazzi
 *ac
*ac
aDepartment of Chemistry “Giacomo Ciamician”, University of Bologna, via Piero Gobetti 85, 40129, Bologna, Italy. E-mail: marco.severi6@unibo.it; daniele.fazzi@unibo.it
bDepartment of Chemistry, Queen Mary University of London, Mile End Road, London, E1 4NS, UK. E-mail: c.b.nielsen@qmul.ac.uk
cDepartment of Chemistry and Biochemistry, Institute for Light and Matter, University of Cologne, Greinstraße 4-6, 50939, Cologne, Germany
First published on 21st October 2025
Abstract
Naphthalene diimide (NDI) based molecules are soft organic functional materials investigated for their n-type semiconducting properties and, recently, for their coupled electronic and ionic transport properties. Such qualities make them potential candidates as mixed ionic-electronic conductors (OMIECs) for electrochemical energy storage devices and bioelectronic sensors. A key aspect is the rationalization of their solid-state structure and morphology, which ultimately controls their transport properties. Here, we introduce two newly synthesized NDIs, namely, NDI-TEG, functionalised with linear triethylene glycol side chains, and NDI-crown, with 15-crown-5 rings. Their bulk structural properties, investigated via experimental characterization and state-of-the-art molecular dynamics (MD) simulations, are compared with those of the parental species NDI-C10, featuring symmetrical n-decyl side chains. Our MD simulations reproduce remarkably well the experimental crystal structures of NDI-C10 and NDI-TEG. At the same time, we compute ex novo the amorphous morphology of NDI-crown, by simulating the experimental film casting conditions. Structural order parameters and correlation functions allow us to gain detailed atomistic insights into both short- and long-range order, as well as to investigate the thermal disorder effects, highlighting the role of the functional side groups. Our study establishes a validated computational ground for modelling NDIs in condensed solid phases, benchmarking the procedure with respect to experimental XRD data, and extending it to amorphous films, thus paving the way for an in-depth understanding of the structure–property functions of small molecule n-type semiconductors.
Introduction
Naphthalene diimide (NDI) based compounds stand out due to their high stability and electron mobility, outperforming other rylene diimide-based systems.1,2 Facile tuning of the lowest unoccupied molecular orbital (LUMO) energy levels provides access to bench-stable materials with high operational stability for application in organic electronic devices and low susceptibility to deleterious side reactions involving, e.g., water and oxygen. Besides being studied for their exceptional supramolecular properties3 and n-type semiconducting characteristics,4 NDIs have recently been investigated as organic mixed ionic-electronic conductors (OMIECs).5OMIECs are a rising and promising class of soft functional materials (conjugated molecules or polymers) able to conduct both ionic and electronic charges (e.g. electrons and holes).6–12 Such coupled conduction mechanisms, together with the facile solution processability and chemical synthesis, have led to the application of OMIECs in devices where the ionic transport is crucial, ranging from organic electrochemical transistors,13–15 light-emitting devices,16–18 optoelectronics,19 and biosensors20 to energy storage systems.21–24
The performance of organic semiconductors, and in particular of OMIECs, is tied to the solid state morphology, which governs among others the water/ion penetration, the ionic and electronic transport properties, and the overall device functionality.11,25 OMIECs’ structure–function rules can be inferred from experimental data. The π-stacking and short-/long-range structural order can enhance the electronic transport, while polar side chains can govern the ionic diffusivity, by influencing the solubility, packing motifs and solvent intake.26,27 However, achieving precise control over the morphology and functionalities of OMIECs remains a critical challenge.23,28–34
Small-molecule OMIECs offer an attractive platform for fundamental investigations.35 In this case, fixing the central π-conjugated chromophore and exploring different functionalisations to the periphery of the system (e.g., side chain variations, halogen substitutions, etc.) provide access to closely related systems with wide-ranging differences in e.g. morphological and electronic characteristics. Notably, NDI-based molecules exhibit a complex morphological landscape.36–38 Depending on the side functional groups, the solid state structures may feature various degrees of order, ranging from crystalline, showing a quite rich and heterogeneous polymorphism, to liquid crystal phases. Paradigmatic examples are NDI-C6 (i.e., n-hexyl side chains), showing at least four different polymorphs, depending on the thermal treatment and deposition method, and NDI-C10, featuring a polymorphic transition followed by a liquid crystal phase close to the melting point.36,37
Despite this rich body of work, the structure–dynamics relationships of NDIs in the solid state remain largely underexplored. We therefore focus on elucidating the morphology and time-correlation dynamics of three NDI derivatives with distinct functionalised side chains. By systematically combining crystallographic characterization and extended molecular dynamics (MD) simulations, we provide atomistic-level insight into how chemical modifications govern the crystalline versus amorphous nature, packing motifs, and local ordering phenomena. Such structural insights are instrumental for interpreting future mixed conduction measurements and serve as an essential benchmark for developing predictive design rules of small-molecule organic conductors.
Starting from the single crystal of NDI-C10,36 symmetrically functionalized with n-decyl side chains, we provided to the best of our knowledge the first all-atom computational study (i.e., force-field molecular dynamics (MD) simulations) of such species, parametrizing the force field at best to reproduce the experimental X-ray diffraction (XRD) data. Following this computational validation, we extended our analysis to two newly synthesised NDI derivatives: NDI-TEG, which incorporates linear triethylene glycol side chains, and NDI-crown, functionalized with 15-crown-5 rings (Scheme 1). The hydrophilic oligoether side chain (such as triethylene glycol) is a popular motif in OMIEC molecular design enabling interactions with hydrated ions, while the cyclic crown ether derivatives offer cation–selective interactions governed by the radius of the crown ether and the ionic radius of the cation.39 These functionalisations draw inspiration from perylene diimide systems,40,41 where similar side groups have shown promising results towards enhancing the ion selectivity as well as the electron transport for mixed ionic-electronic conductor applications. NDI-TEG is highly crystalline, while NDI-crown is amorphous as confirmed by thin-film X-ray diffraction (see the SI, Fig. S9). Our extended atomistic MD simulations successfully reproduce the experimental crystal structure of NDI-TEG and, at the same time compute ex novo the amorphous morphology of NDI-crown. Finally, through a combined use of structural order parameters and correlation functions, we characterize both short- and long-range order of each NDI species in the solid state, thus paving the way for an in-depth understanding of their structure–property functions towards their use as organic mixed ionic and electronic conductors.
Methods
Details about the experimental methods (e.g., materials, synthesis, thermogravimetric analysis, differential scanning calorimetry, and X-ray diffraction data) are provided in the SI.Molecular dynamics simulations
MD simulations were performed using LAMMPS-2Aug202342,43 on supercells of NDI-C10, NDI-TEG and NDI-crown. The bonded parameters were taken from the OPLS-AA force field (version 2020),44 which has been already employed in several MD studies on OMIECs.45–49 Bonds involving hydrogen atoms were constrained using the SHAKE algorithm.50 The usage of appropriate force constants ensured the planarity of the NDI core. The supercell for NDI-C10 has dimensions of 8 × 8 × 8 (containing 512 molecules), generated from the experimental XRD structure taken from the Cambridge Crystallographic Data Centre (CCDC 1972224).36 To reproduce the single crystal structure via MD simulations, a careful re-parametrization of some force field terms is generally required. In this study, we re-parametrized the non-bonded terms via the following procedure. The non-bonded (e.g., van der Waals) parameters were obtained in two ways: (i) using standard values, as provided by OPLS-AA/2020, and (ii) using recomputed values, obtained by following the procedure reported in ref. 51–53, that is, performing quantum chemical calculations to derive appropriate partial charges (vide infra) and effective volume of the atoms and then applying the Tkatchenko–Scheffler (T–S) method.51–53 The quantum chemical calculations were performed using Gaussian1654 considering the ωB97X-D2 range separated functional and the def2-TZVPP basis set.55–57 The NDI-C10 (single molecule) structure was optimized starting from the XRD geometry (CCDC 1972224).36 The partial charges were evaluated using two population analysis schemes, namely, CHELPG and DDEC6 (density-derived electrostatic and chemical electron density partitioning).58–61 DDEC6 charges were computed using the Chargemol program. We ran four sets of MD simulations by exploiting all different combinations between non-bonded parameters and partial charges (that is, OPLS with standard non-bonded parameters and either CHELPG or DDEC6 atomic charges and OPLS with recomputed non-bonded parameters via the Tkatchenko–Scheffler (T–S) method (here named OPLS/T–S) and either CHELPG or DDEC6 atomic charges).After energy minimisation, the system was equilibrated in the NVT ensemble at 300 K for 1 ns. A Nosé–Hoover thermostat was used with a time constant of 0.2 ps. The MD integration time step was 2 fs. For the Coulomb interactions, the particle–particle–particle–mesh method for long-range electrostatics was used, and the van-der-Waals and Coulomb cut-offs were set to 1.2 nm. Then, a 20 ns simulation was performed in the NPT ensemble with a Nosé–Hoover barostat and Martyna, Tuckerman, and Klein correction, at 300 K and 1 atmosphere, with a time constant of 2 ps. The barostat was first set such that only isotropic cell fluctuations were allowed, that is, the cell angles are constrained and the dilations/compressions are coupled in all three directions (iso keyword in LAMMPS). By constraining the crystal cell to isotropic variations, we can isolate the contribution of the non-bonded parameters and atomic charges on the resulting mass density. The properties were finally averaged over the last 10 ns. After this first validation phase, the protocol that better reproduced the NDI-C10 density (i.e. OLPS/T–S and DDEC6 charges) was applied to both NDI-C10 and NDI-TEG, this time with anisotropic cell fluctuations for the production runs.
For NDI-TEG, we considered a 5 × 5 × 5 supercell (each unit cell contains 4 molecules, in such a way that a similar number of molecules to those for NDI-C10 are considered in the MD simulations) starting from the experimental XRD structure, as derived in this work. The non-bonded parameters have been computed using the T–S method, and the partial charges using the DDEC6 scheme. After energy minimisation, the system was heated in the NVT ensemble from 0 K to 300 K for 3 ns. A subsequent equilibration in the NVT ensemble at 300 K was performed for 1 ns. With respect to the benchmarking protocol defined above, we introduced a gentle heating from 0 K to 300 K for 3 ns to minimise the morphology fluctuations in the NVT ensemble. Production run was performed in the NPT ensemble at 300 K and 1 atmosphere for 20 ns. Triclinic cell fluctuations were allowed with the keyword tri in LAMMPS. The time constants of the thermostat and barostat are the same as defined above.
For NDI-crown, we employed a similar simulation protocol as reported in ref. 62 to generate an amorphous thin film morphology as obtained from deposition of chloroform solution.62–64 The force field employed is the same as that used for NDI-C10 and NDI-TEG (OPLS/T–S with DDEC6). After energy minimisation, the system (500 molecules in the simulation box) was heated from 0 K to 500 K in 5 ns using a Langevin thermostat and a Nosé–Hoover barostat, setting the pressure to 1 atmosphere and the time constant to 2 ps. The damping parameter of the Langevin thermostat was 3.8 ps.62 The dielectric constant of chloroform, 4.81, was employed to scale the electrostatic interactions. Subsequently, the system was simulated for 30 ns at 500 K and then cooled from 500 K to 300 K in 5 ns, with the same setting used during the heating process. The final production run was performed in the NPT ensemble for 30 ns, using a Nosé–Hoover thermostat and barostat, at 300 K and 1 atmosphere, and the dielectric constant was set to 1.0.
Structural analyses
The radial distribution functions (RDFs) considering the nitrogen atom belonging to NDI pairs and dihedral distribution functions (DDF) (see Scheme 1 for the definition of the dihedral angles considered in our analysis) were computed using the code TRAVIS.65,66 The molecular orientational order parameter Q was also considered to study the long range orientational order. Q is defined as the largest eigenvalue of the Saupe ordering matrix Qαβ,67–73 namely, | (1) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0075_20d1.gif) (i)α is a vector describing the molecular orientation and the indices α and β run over the three cartesian coordinates (x, y, z), that is, over the three vector components. Q ranges from 1, when all molecules are oriented in the same direction and the system is perfectly ordered, to 0, when all molecules are randomly oriented and the system is disordered. The orientational order parameter was computed using MDTraj.74
(i)α is a vector describing the molecular orientation and the indices α and β run over the three cartesian coordinates (x, y, z), that is, over the three vector components. Q ranges from 1, when all molecules are oriented in the same direction and the system is perfectly ordered, to 0, when all molecules are randomly oriented and the system is disordered. The orientational order parameter was computed using MDTraj.74
Results and discussion
NDI-C10
We focus on the room temperature polymorph of NDI-C10, the only species investigated in this study that has already been reported in the literature,36 which shows a triclinic unit cell. The NDI cores are stacked in layers separated by the side chains, with the latter adopting an all-trans conformation, as shown in Fig. 1. | ||
| Fig. 1 Experimental NDI-C10 crystal structure.36 Lattice vectors (a, b, c) are given in red, green and blue, respectively. View along the b vector (panel a) and from the c vector (panel b). | ||
At first, we validated the atomistic force field based on the experimental XRD data. As reported in the Methods section, we relied on the OPLS/2020 (from now on OPLS) for the bonded parameters by describing here only the fundamental role played by the non-bonded parameters and atomic charges in determining the structural and thermodynamic properties of crystalline NDI-C10. Aiming at reproducing the experimental crystal density, we tested four combinations in our MD simulations, namely, OPLS with standard non-bonded parameters and either CHELPG or DDEC6 atomic charges, OPLS with recomputed non-bonded parameters via the Tkatchenko–Scheffler (T–S) method (OPLS/T–S) and either CHELPG or DDEC6 atomic charges. While the OPLS non-bonded parameters and the CHELPG charges are extensively used in the literature, the recomputed T–S non-bonded parameters together with the DDEC6 scheme have been only recently proved to be successful in reproducing the elusive glass transition temperature in polymers51 and in the simulation of biomolecules.53 In our force field validation phase, we restricted the cell to isotropic fluctuations, constraining the crystal cell angles to their experimental value. In this way, we can isolate the contribution of the non-bonded parameters and atomic charges to the calculation of the density. Main results are summarized in Table 1.
| CHELPG | DDEC6 | |
|---|---|---|
| OPLS | 1.145 (2.93%) | 1.144 (2.93%) |
| OPLS/T–S | 1.214 (2.93%) | 1.185 (0.51%) |
| Experimental density36 | 1.179 |
The usage of standard OPLS non-bonded parameters underestimates the densities, which are almost insensitive to the choice of the atomic charges. Instead, the recomputed non-bonded parameters (OPLS/T–S) in combination with the CHELPG charges overestimate the density, while their combination with the DDEC6 produces the best match with the experimental data, leading to a supercell density equal to 1.185 g cm−3, that is, a 0.51% deviation from the experimental value of 1.179 g cm−3. Considering the above results, we found that our reparametrized OPLS/T–S force field, in combination with DDEC6 charges, can be considered the best interaction potential for reproducing NDI experimental data, and therefore, we considered it for all of the following simulations.
Once the force field was benchmarked, we ran a production simulation in which the cell edges and angles can vary independently. In this MD trajectory, we performed the structural analyses reported in Fig. 2.
 | ||
| Fig. 2 Structural analyses of the simulated NDI-C10 crystal structure (MD data, orange), compared to the experimental XRD data (blue). Panel (a): radial distribution function (RDF) between nitrogen atoms. Panel (b): ϑ angle (C1–N2–C3–C4, see Scheme 1) dihedral distribution function (DDF) (full width at half maximum – FWHM – equal to 25° for both peaks), and panel (c): ϕ angle (C6–C7–C8–C9) DDF (FWHM equal to 25°). Panel (d): order parameter Q (eqn (1)) computed considering three schemes: orientation of only the molecular cores (violet data), orientation of only the –C10 side chains (green data), or orientation of the whole molecule (brown data). | ||
The MD computed radial distribution function (RDF, Fig. 2a) nicely overlaps with the one computed for the experimental crystal structure (XRD), proving the effectiveness of our simulation protocol (anisotropic cell variations) and the validity of the re-parameterized force field (OPLS/T–S, DDEC6) in reproducing the NDI-C10 crystal structure. The computed principal peak, representing the first coordination shell between nitrogen atoms belonging to nearest-neighbour NDI pairs, slightly down shifts with respect to the experimental value, which is 4.48 Å (MD) vs. 4.75 Å (XRD) (Fig. 2a). This is ascribable to a slight volume compression with respect to the experimental cell reflected in a small increase of the mass density (1.263 g cm−3 from MD vs. 1.179 g cm−3 from XRD). The a and c cell vectors slightly shrink by 5.55% and 4.10%, respectively, with vector a representing the direction of the π–π stacking. Cell vector b undergoes a 3.55% dilation. The deviation of the computed RDF peaks around 16 Å is due to the compression along the c vector.
Concerning the side chain conformations along with the dynamics, the dihedral angle ϑ governs the direction of the alkyl chains with respect to the NDI core (C1–N2–C3–C4, Scheme 1). Its dihedral distribution function (DDF), reported in Fig. 2b, shows two peaks since the two side chains are oppositely oriented with respect to the NDI plane (Fig. 1). The position of the experimental and simulated peaks is the same, lying at 90° and 270°, and the full width at half height of the distribution is equal to 25° for both peaks, showing that the impact of the thermal disorder (T = 300 K) on the simulation cell is limited to a broadening with respect to the equilibrium value and does not promote the population of other conformers. The same considerations apply to the dihedral angle ϕ (C6–C7–C8–C9, Scheme 1), which describes the local orientations of the terminal methyl groups. Our MD simulation reproduces the experimental peak distribution at 180° (Fig. 2c), with the width at half height equal to 25°, as for ϑ. The dihedral distribution functions of other torsional angles are reported in the SI (Fig. S10). Notably, the ζ angle distribution nicely reproduces the experimental data, proving that the all-trans chain conformation is maintained throughout the dynamics. Our finite temperature MD simulation supports the experimental crystal data for NDI-C10 (see also Table S6, SI), showing stacked NDI units with fully extended alkyl chains, preserving their full extension even at 300 K, and therefore being resilient to thermal induced disorder effects at room temperature.
Finally, we evaluate the global orientational order by computing the nematic order parameter Q (eqn (1)) throughout the entire simulation cell, over the MD production run (i.e., 20 ns). Q was computed in three different schemes, as reported in Fig. 2d, namely, by considering (a) only the atoms belonging to the NDI cores (violet data), (b) only the atoms of the side chains (green data), or (c) the atoms of the whole molecule (brown dotted data). For each case, the Q is higher than 0.996 during the entire MD production run, revealing that the temperature does not affect the orientational ordering of the NDI cores, the side chains nor the overall crystal structure.
The perfect match between the experimental and MD based data proves that our MD methodology produces a state-of-the-art description for the NDI-C10 crystal cell at room temperature.
NDI-TEG
Following synthesis and crystal growth by slow cooling of a hot concentrated solution in methanol, we successfully obtained a single crystal structure of NDI-TEG by X-ray diffraction (see the SI for further details and Tables S1–S5). At room temperature, NDI-TEG is characterised by a monoclinic crystal lattice, as depicted in Fig. 3. The NDI cores are stacked in a columnar fashion along the b axis. Notably, two neighbouring NDI cores along the crystallographic c axis are oriented in opposite directions, one molecule towards the a–c plane and the other away from the a–c plane (Fig. 3b). The triethylene glycol side chains show a peculiar conformation, far from the all-trans conformation of the parent alkyl-based NDI-C10 species. In NDI-TEG side chains, only two dihedrals, the third and fifth, are close to 180°, while the others adopt different conformations. In the solid state, this unique side-chain conformation enables the NDIs to closely pack uniformly in all three dimensions without creating, in contrast to NDI-C10, a lamellar structure characterized by alternating layers of NDI planes and side chains.To gain atomistic insights into the NDI-TEG crystal structure, we employed the same MD simulation protocol as that benchmarked on NDI-C10. Remarkably, for NDI-TEG, we were able to reproduce the experimental density of 1.376 g cm−3 with only a 2.48% overestimation. Notably, the variations in the cell angles are less than 0.1% (SI, Table S7), while the changes in the b and c cell edges are under 1%. Only the cell vector a exhibits a larger variation of 2.80%. Fig. 4 shows the RDF, DDF and Q order parameter analyses for NDI-TEG, similar to that reported for NDI-C10 in Fig. 2.
 | ||
| Fig. 4 Structural analyses of the simulated NDI-TEG crystal structure (MD data, orange), compared to the experimental XRD data (blue). Panel (a): RDF between nitrogen atoms. Panel (b): ϑ angle (C1–N2–C3–C4, see Scheme 1) DDF (FWHM equal to 12° and 14°) and panel (c): ϕ angle (C6–C7–C8–C9) DDF (FWHM equal to 30°). Panel (d): order parameter Q (eqn (1)) computed considering three schemes: orientation of only the molecular cores (violet data), orientation of only the TEG side chains (green data), or orientation of the whole molecule (brown data). | ||
The comparison between the MD computed and experimental RDFs is quite remarkable (Fig. 4a), showing a perfect agreement between the two. The first principal peak is computed at 4.48 Å, close to the experimental value of 4.45 Å. A good agreement with the experimental results is also obtained for the ϑ angle DDF (Fig. 4b), which describes the rotation around the bond connecting the side chains and the NDI core (Scheme 1). The ϑ DDF of the crystal structure presents four peaks, two at 80° and 100° and two at 260° and 280°, respectively. This splitting is simply due to the choice of the frame of reference. In the crystal cell, two neighbouring cores have different orientations and the consequence is that the ϑ angle assumes two opposite values. In one molecule, the ϑ is 80° for one chain and 280° for the other side chain, and in the neighbouring molecule, the ϑ is 100° and 260°. The peaks computed from the MD trajectory deviate at most by 4° from the experimental value and the full width at half height of the four peaks is between 12° and 14°. The terminal dihedral angle of the TEG chains, ϕ, is more elusive (Fig. 4c). In the crystal structures, the ϕ can be 165° or 195°, and during the finite temperature MD simulation, the ϕ assumes the average value of 180° and the associated peak has a full width at half height of 30°. The thermal effects during the MD average the distribution of the principal peak and promote two smaller peaks at 85° and 276° (Fig. 4c). Also, the ζ angle, the first dihedral angle that influences the conformation of the side chain (Scheme 1), is in good agreement with the XRD data (Table S7 and Fig. S11, SI), reproducing the gauche and gauche prime orientations of the side chain.
Despite these thermal effects, the nematic order parameter Q confirms the overall reproduction of the experimental crystal cell structure (Fig. 4d). The ordering of the side chains and of the entire molecules is remarkably close to the crystal experimental case, showing a Q larger than 0.98. The Q parameter computed considering only the NDI cores can reach at most the value of 0.5, since two neighbouring cores have opposite spatial orientation in the experimental crystal cell. In our simulation, the Q parameter of the cores is close to 0.5 and thus the spatial order of the cores is perfectly maintained throughout the entire dynamics at 300 K.
NDI-crown
After synthesis, all attempts at growing a suitable single crystal of NDI-crown were unsuccessful, implying that the morphology cannot be determined through XRD measures at present (see the details in the SI, Fig. S9). Insights into its atomistic structure can, however, be obtained using our MD simulations, having re-parametrized and benchmarked the force field for both NDI-C10 and NDI-TEG derivatives. In such a way, it would be possible to generate reasonable morphologies for the amorphous phase. Here, we employed the previous parametrization scheme to simulate an NDI-crown thin film deposited from chloroform, reflecting typical experimental conditions. The resulting amorphous morphology is shown in Fig. 5, while the structural analyses on the computed morphology are shown in Fig. 6. | ||
| Fig. 6 Structural analyses of the simulated NDI-crown amorphous structure. Panel (a): RDF between nitrogen atoms. Panel (b): ϑ angle (C1–N2–C3–C4, see Scheme 1) DDF (FWHM equal to 27° and 30°). Panel (c): histogram of the ratio between two axes (axis 1 (red) and axis 2 (blue)) of the 15-crown-5 ring. Panel (d): spatial correlation function C(r) (eqn (3)) of the fluctuations of the vectors parallel (blue) and normal (orange) to the NDI core (see also blue and red vectors in Fig. 5). The vertical dotted line marks the loss of short range order. | ||
The resulting density of the simulation cell is 1.304 g cm−3, similar to the NDI-TEG density. The RDF (Fig. 6a) confirms that the structure is amorphous, characterized by a lack of long-range structural order. In such a scenario, the analysis of the ϑ angle is especially relevant (Fig. 6b). First, the two peaks located at 97° and 281° present a full width at half height equal to 30° and 27°, respectively, and are skewed towards smaller values with respect to the centre of the peak. The broadening is higher than the counterpart evaluated for NDI-C10 and NDI-TEG, indicating that thermal disorder effects on the 15-crown-5 side chains are slightly higher than the ones on the n-decyl and triethylene glycol chains. Moreover, the ϑ angle governs whether the 15-crown-5 motifs are placed either at the same side with respect to the NDI plane (syn isomer) or at opposite sides with respect to the NDI plane (anti isomer), see SI Fig. S14 for a structural representation of the isomers. We found that our simulation time (30 ns at 500 K and 30 ns at 300 K) is sufficient to obtain a stable syn/anti distribution, converging to 48% molecules in syn and 52% in anti.
To better characterize the structural properties of NDI-crown, we check the circular aspect ratio (roundness) of the crown ether side chain, namely, the ratio between the two inner-circle axes (axis 1 and axis 2), as defined in Fig. 6c. Such geometrical properties are fundamental since the size and shape of the crown ethers influence, for instance, the binding selectivity to ions.75 The distribution of the axis 1/axis 2 ratios (Fig. 6c) shows a mean value equal to 1.067, with a standard deviation of 0.200. The mean value of axis 1 is 5.95 Å, while the mean value of axis 2 is 5.69 Å, indicating that during the dynamics, the 15-crown-5 motif nicely approximates the shape of a circle, maintaining its roundness. It must be noticed that in the calculation of the radii, the atoms are treated as points, not considering the van der Waals radii.
Given the overall lack of long-range structural order, as proven by the RDF (Fig. 6a) and by the calculation of the nematic order parameter Q which is close to zero (Fig. S12, SI), we investigate the local dynamics and structural correlation between the NDI cores to gain insights into their short-range order and collective dynamics of NDI-crown.
To this aim, we resort to the analysis of structure-based correlation functions as introduced by Cavagna et al. studying general disordered systems,76 ranging from glasses to living systems, such as bacteria and bird flocks. In ref. 76, Cavagna et al. studied the local and collective spatial behaviour of birds within a flock during the fly time. We translate such an approach to describe how the movement of a molecule is correlated with another one within the amorphous phase, thus solving their collective spatial dynamics. We start by defining the behavioural state to observe considering a vector parallel to the NDI core (i.e., connecting the two nitrogen atoms, see the blue arrow in Fig. 5b) and a vector normal to the NDI core (see the red arrow in Fig. 5b). This vector dyad describes the orientation of the NDI plane in space. The fluctuation vector (![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0066_20d1.gif) i) of a specific NDI core (named here, site i) around the positional mean computed for all NDIs (N) is defined as
i) of a specific NDI core (named here, site i) around the positional mean computed for all NDIs (N) is defined as
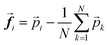 | (2) |
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0066_20d1.gif) i indicates that the positional orientation of a molecule (
i indicates that the positional orientation of a molecule (![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) i) is considerably different from the average orientation of the whole system (called polarization in ref. 76). To study possible correlations occurring between local positional fluctuations of NDIs, the spatial correlation function of the fluctuated vectors is computed as follows:
i) is considerably different from the average orientation of the whole system (called polarization in ref. 76). To study possible correlations occurring between local positional fluctuations of NDIs, the spatial correlation function of the fluctuated vectors is computed as follows: | (3) |
Fig. 6d depicts the computed C(r) as defined in eqn (3), for both parallel (Cp(r), blue data) and normal (Cn(r), orange data) NDI vectors. For short distances, smaller than 5 Å, the structural fluctuations of the vectors parallel to the cores are correlated (Cp(r) > 0), while those of the normal vectors are anticorrelated (Cn(r) < 0). A positive correlation of Cp(r) implies the existence of molecular aggregates where the NDI cores tend to be aligned in the same direction (in-plane correlation). Such aggregate configurations can be achieved via either a π–π stacking of the NDI plane (Fig. 5c) or an edge-on packing (Fig. 5d), where the NDI cores are perpendicular to each other, still maintaining the long axis vectors (blue vector, Fig. 5b) parallel. This finding reveals the existence of a short-range structural order between the NDI cores. The negative values for Cn(r) reflect an anticorrelation between the normal vectors of NDIs, thus implying a short-range order, however, with vectors pointing in opposite directions. Both Cp(r) and Cn(r) suggest that on average across the bulk NDI-crown self-organizes into local aggregates (e.g., dimers and trimers) with packing motifs that can range from π–π, edge-on or tilted stacking. For distances larger than 5 Å, both Cp(r) and Cn(r) decay to small values, close to zero, indicating the absence of spatial correlation and therefore long-range disorder.
Comparative analysis
Having fully characterized the short- and long-range structural order of NDI-C10, NDI-TEG and NDI-crown, we now compare the three species with a view to emphasise some preliminary structure–property functions. In Fig. 7, we report the radial distribution function, the coordination number and the dihedral distribution function of each system to underline different structural properties of NDIs, ultimately related to their molecular structure.From the comparison of the RDFs (Fig. 7a) clearly emerges the amorphous nature of NDI-crown compared to the crystalline structural order of NDI-C10 and NDI-TEG. For both NDI-C10 and NDI-TEG, the principal peak is located at the same distance (4.48 Å), thus reflecting similar nearest neighbour proximity between the NDI moieties for two such species. NDI-C10 shows sharper and more intense peaks than NDI-TEG, indicating tighter molecular packing and reduced influence of thermal disorder. In contrast, the broad and weak features of NDI-crown confirm its amorphous morphology. The amorphous NDI-crown, unlike the other two crystals, presents a tail of the radial distribution function, which extends to lower distances than NDI-C10 and NDI-TEG. The structures contributing to such a tail are represented by dimer-like aggregates where the intermolecular distance between the NDI cores is lower than 4 Å, corresponding to roughly 7–8% of the molecules in the simulation box. Such an aspect is quite remarkable because, despite the limited number of molecules featuring the closely packed structure, it shows that a structurally hindered species like the NDI-crown can still lead to inter-molecular distances which are even lower than those obtained by linear side chains, like C10 and TEG. The integral of the RDF (Fig. 7b) shows a dimer-like interaction up to 6 Å for NDI-C10 and NDI-TEG. The integral of the RDF also shows that NDI-C10 is the closest packed structure throughout the whole simulation box. Interestingly, each molecule of NDI-TEG and NDI-crown has the same number of neighbouring molecules at a radius of 10 Å, despite the differences in the chemical structure and short-range morphology.
The equilibrium value of the ϑ angle (Fig. 7c), governing the position of the side group, falls in the same region; however, it presents some differences for the three species. Most notably, due to the symmetry of the crystal cell, NDI-TEG shows four peaks, while NDI-C10 and NDI-crown show only two. In NDI-TEG, the ϑ angle is stiffer compared to the other two species, as reflected by the full width at half height of the peaks being 12–14°, while for NDI-C10 and NDI-crown, it ranges from 25° to 30°. This aspect might reflect larger thermal disorder effects for NDI-C10 and NDI-crown than for NDI-TEG. On the other hand, the ζ angle (Fig. 7d) highlights the difference between morphologies. For crystalline NDI-C10 and NDI-TEG, the peaks are centred around the experimental values and the effect of thermal disorder is comparable to the ϑ angle case. For NDI-crown, on the other hand, the ζ angle shows the morphological versatility of the amorphous phase. The three peaks are centred at 56°, 183° and 302° and the thermal effects are higher with respect to those affecting the ϑ angle, proving a wider exploration of the phase space.
The above structural analyses provide some understanding about the overall conformational versatility; however, they cannot give insights into the inner dynamics and time scales, reflecting possible time-dependent structural relaxations. To include dynamical information, we investigated some inner structural changes via a time-dependent correlation function largely used in the analysis of liquid (disordered) systems, showing how fast the memory of a molecular orientation is lost.77,78 The latter is the time required for the molecules to lose their initial configuration, called the reorientation time (see the SI for details about the computation of the correlation function). For NDI-C10 and NDI-TEG, we witness hindered rotational dynamics (i.e., constant correlation function), typical of rigid crystal structures (Fig. S13, SI). Interestingly, for NDI-crown, the rotational dynamics of both the naphthalene cores and the crown motifs are partially allowed, so the reorientation correlation function rapidly decays in the first 5 ns, though maintaining a high value (>0.90) still after 30 ns dynamics. Full reorientation, if any, might occur, however, on a timescale much longer than our capable computing time, suggesting a rigid, glassy-like state.79
Overall, the amorphous NDI-crown shows richer conformational versatility with respect to its crystalline NDI-C10 and NDI-TEG counterparts. This versatility, however, could be related to the simulated deposition process, which produces a (meta)stable state in which the internal dynamics are hindered.
Conclusions
In this work, we performed extended molecular dynamics (MD) simulations on three NDI species, namely, the well-known NDI-C10 (functionalized with n-decyl side chains), as the reference compound, and two newly synthesized NDIs, which are potential candidates for OMIECs: NDI-TEG (with linear triethylene glycol side chains) and NDI-crown (with cyclic 15-crown-5 motifs). The three species have been synthesized and experimentally characterized. NDI-C10 and NDI-TEG result in crystalline forms at room temperature, while NDI-crown appears amorphous in the solid state. To gain quantitative insights into the structural order at the molecular scale, we performed MD simulations by carefully re-parameterizing the non-bonded parameters of the force field. Such an approach results in a remarkable match between simulated and experimental single-crystal data for NDI-C10 and NDI-TEG, leading to an overestimation of only 1–2% in the MD computed mass density and crystal cell parameters.At room temperature, NDI-C10 single-crystals show a lamellar stacking motif with close packed NDI cores and perpendicular side chains showing an all-trans conformation. Thermal disorder does not trigger significant sliding or rotations of the NDI cores, nor does it introduce gauche-like conformations within the side chains, as confirmed by a high nematic global order parameter (Q > 0.99).
NDI-TEG, instead, forms a columnar arrangement in which neighbouring cores along the c axis adopt opposite orientations. The triethylene glycol side chains are normal to the NDI unit; however, they show a mixed gauche–trans conformation, similar to that of other semiconducting small molecules for p-type organic electrochemical transistors.29 This unique chain conformation allows for a dense molecular packing, without forming lamellar layers. Thermal fluctuations slightly broaden the dihedral angle distributions; however, the overall structure is maintained, as reflected by high Q values (>0.98).
Replicating the experimental conditions, our MD simulations were able to predict the solid-state morphology of NDI-crown, which was found to be amorphous. Accordingly, Q is close to zero. Despite a disordered bulk, NDI-crown shows some short-range structural order. We characterized the order by introducing a spatial correlation function, previously considered in the field of correlated complex systems, finding that on a short-range length scale, NDI-crown self-organizes into local aggregates (e.g., dimers and trimers), with packing motifs varying from π–π, edge-on or tilted stacking.
Finally, time-dependent orientational auto-correlation functions revealed the high structural stiffness of each species, however, showing a higher rotational degree of freedom for NDI-crown than for NDI-C10 and NDI-TEG. Such a feature suggests the existence of possible metastable (glassy-like) states, otherwise impossible to capture using standard MD simulation techniques, suggesting the use of advanced enhanced sampling methods for their investigation.80
Our joint experimental and computational investigation shows that linear and crown glycol side chains can have a profound impact on the bulk morphology of the NDIs. The first leads to highly crystalline materials with hindered internal dynamics, while the second results in amorphous films showing a local degree of molecular ordering and correlation dynamics. Such a structure-dynamic property may pave the way for further systematic analysis aiming at designing guidelines for electronic and ionic transport properties in small-molecule conductors.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5tc02399h.Technical data can be found also in attached files.
CCDC 2456282 contains the supplementary crystallographic data for this paper.81
Acknowledgements
S. Y. and C. B. N. acknowledge funding from the European Union Horizon Europe under EC Grant Agreement 101129638 and UK Research and Innovation (UKRI) under the UK government's Horizon Europe funding guarantee [grant number 10104091]. D. F. acknowledges the DFG Research Training Group 2591 ‘‘Template-designed Organic Electronics (TIDE)’’, the Global Faculty Program of the University of Cologne within the focus area ‘‘Quantum Matter and Materials (QM2)’’, the National Recovery and Resilience Plan (NRRP), Mission 04 Component 2 Investment 1.5 – NextGenerationEU, Call for tender no. 3277 dated 30/12/2021, Award Number: 0001052 dated 23/06/2022, and the National Project funded by the European Union – Next Generation EU, Project title ‘‘Modelling and design of organic conjugated redox materials for energy-saving applications: a bottom-up strategy’’, code MUR 2022WKTH9E – CUP J53D23008810006. D. F. and M. S. thank Dr A. Giovine from the Department of Computer Science and Engineering of the University of Bologna for providing full support in the usage of the High-Performance Computing service cluster of the University of Bologna.References
- A. Nowak-Król, K. Shoyama, M. Stolte and F. Würthner, Chem. Commun., 2018, 54, 13763–13772 RSC.
- X. Zhan, A. Facchetti, S. Barlow, T. J. Marks, M. A. Ratner, M. R. Wasielewski and S. R. Marder, Adv. Mater., 2011, 23, 268–284 CrossRef CAS.
- S. V. Bhosale, C. H. Jani and S. J. Langford, Chem. Soc. Rev., 2008, 37, 331–342 RSC.
- S. V. Bhosale, M. A. Kobaisi, R. W. Jadhav, P. P. Morajkar, L. A. Jones and S. George, Chem. Soc. Rev., 2021, 50, 9845–9998 RSC.
- S. Kang, J. Fan, J. B. P. Soares and M. Gupta, RSC Adv., 2023, 13, 5096–5106 RSC.
- S. V. Bhosale, M. A. Kobaisi, R. W. Jadhav, P. P. Morajkar, L. A. Jones and S. George, Chem. Soc. Rev., 2021, 50, 9845–9998 RSC.
- M. Al Kobaisi, S. V. Bhosale, K. Latham, A. M. Raynor and S. V. Bhosale, Chem. Rev., 2016, 116, 11685–11796 CrossRef PubMed.
- A. Giovannitti, C. B. Nielsen, D.-T. Sbircea, S. Inal, M. Donahue, M. R. Niazi, D. A. Hanifi, A. Amassian, G. G. Malliaras, J. Rivnay and I. McCulloch, Nat. Commun., 2016, 7, 13066 CrossRef CAS PubMed.
- B. D. Paulsen, K. Tybrandt, E. Stavrinidou and J. Rivnay, Nat. Mater., 2020, 19, 13–26 CrossRef CAS.
- P. Gkoupidenis, Y. Zhang, H. Kleemann, H. Ling, F. Santoro, S. Fabiano, A. Salleo and Y. van de Burgt, Nat. Rev. Mater., 2024, 9, 134–149 CrossRef CAS.
- J. Rivnay, S. Inal, A. Salleo, R. M. Owens, M. Berggren and G. G. Malliaras, Nat. Rev. Mater., 2018, 3, 1–14 CrossRef.
- S. Fabiano, L. Flagg, T. C. H. Castillo, S. Inal, L. G. Kaake, L. V. Kayser, S. T. Keene, S. Ludwigs, C. Muller, B. M. Savoie, B. Lüssem, J. L. Lutkenhaus, M. Matta, D. Meli, S. N. Patel, B. D. Paulsen, J. Rivnay and J. Surgailis, J. Mater. Chem. C, 2023, 11, 14527–14539 RSC.
- J. T. Friedlein, R. R. McLeod and J. Rivnay, Org. Electron., 2018, 63, 398–414 CrossRef CAS.
- H. Dai and W. Yue, Adv. Eng. Mater., 2024, 26, 2301860 CrossRef CAS.
- M. Moser, J. F. Ponder Jr., A. Wadsworth, A. Giovannitti and I. McCulloch, Adv. Funct. Mater., 2019, 29, 1807033 CrossRef.
- A. van Dijken, A. Perro, E. A. Meulenkamp and K. Brunner, Org. Electron., 2003, 4, 131–141 CrossRef CAS.
- L. Edman, M. A. Summers, S. K. Buratto and A. J. Heeger, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 115212 CrossRef.
- P. Matyba, K. Maturova, M. Kemerink, N. D. Robinson and L. Edman, Nat. Mater., 2009, 8, 672–676 CrossRef CAS.
- Q. Pei, G. Yu, C. Zhang, Y. Yang and A. J. Heeger, Science, 1995, 269, 1086–1088 CrossRef CAS.
- A. Marks, S. Griggs, N. Gasparini and M. Moser, Adv. Mater. Interfaces, 2022, 9, 2102039 CrossRef CAS.
- Y. Liang, Z. Tao and J. Chen, Adv. Energy Mater., 2012, 2, 742–769 CrossRef CAS.
- G. A. Snook, P. Kao and A. S. Best, J. Power Sources, 2011, 196, 1–12 CrossRef CAS.
- D. Moia, A. Giovannitti, A. A. Szumska, I. P. Maria, E. Rezasoltani, M. Sachs, M. Schnurr, P. R. F. Barnes, I. McCulloch and J. Nelson, Energy Environ. Sci., 2019, 12, 1349–1357 RSC.
- J. Kim, Y. Kim, J. Yoo, G. Kwon, Y. Ko and K. Kang, Nat. Rev. Mater., 2023, 8, 54–70 CrossRef.
- A. Baggioli, M. Casalegno, G. Raos, L. Muccioli, S. Orlandi and C. Zannoni, Chem. Mater., 2019, 31, 7092–7103 CrossRef CAS.
- A. Welford, S. Maniam, E. Gann, X. Jiao, L. Thomsen, S. J. Langford and C. R. McNeill, Org. Electron., 2019, 75, 105378 CrossRef CAS.
- N. A. Kukhta, A. Marks and C. K. Luscombe, Chem. Rev., 2022, 122, 4325–4355 CrossRef CAS PubMed.
- F. D. Tsourtou, E. N. Skountzos, S. D. Peroukidis and V. G. Mavrantzas, Soft Matter, 2018, 14, 8253–8266 RSC.
- Z. S. Parr, R. B. Rashid, B. D. Paulsen, B. Poggi, E. Tan, M. Freeley, M. Palma, I. Abrahams, J. Rivnay and C. B. Nielsen, Adv. Electron. Mater., 2020, 6, 2000215 CrossRef CAS.
- N. Siemons, D. Pearce, C. Cendra, H. Yu, S. M. Tuladhar, R. K. Hallani, R. Sheelamanthula, G. S. LeCroy, L. Siemons, A. J. P. White, I. McCulloch, A. Salleo, J. M. Frost, A. Giovannitti and J. Nelson, Adv. Mater., 2022, 34, 2204258 CrossRef CAS.
- S. T. Keene, J. E. M. Laulainen, R. Pandya, M. Moser, C. Schnedermann, P. A. Midgley, I. McCulloch, A. Rao and G. G. Malliaras, Nat. Mater., 2023, 22, 1121–1127 CrossRef CAS PubMed.
- A. Khot and B. M. Savoie, J. Polym. Sci., 2022, 60, 610–620 CrossRef CAS.
- S. T. Keene, V. Gueskine, M. Berggren, G. G. Malliaras, K. Tybrandt and I. Zozoulenko, Phys. Chem. Chem. Phys., 2022, 24, 19144–19163 RSC.
- A. Giovannitti, I. P. Maria, D. Hanifi, M. J. Donahue, D. Bryant, K. J. Barth, B. E. Makdah, A. Savva, D. Moia, M. Zetek, P. R. F. Barnes, O. G. Reid, S. Inal, G. Rumbles, G. G. Malliaras, J. Nelson, J. Rivnay and I. McCulloch, Chem. Mater., 2018, 30, 2945–2953 CrossRef CAS PubMed.
- C. J. Kousseff, R. Halaksa, Z. S. Parr and C. B. Nielsen, Chem. Rev., 2022, 122, 4397–4419 CrossRef CAS PubMed.
- S. Milita, F. Liscio, L. Cowen, M. Cavallini, B. A. Drain, T. Degousée, S. Luong, O. Fenwick, A. Guagliardi, B. C. Schroeder and N. Masciocchi, J. Mater. Chem. C, 2020, 8, 3097–3112 RSC.
- I. de O. Martins, F. Marin, E. Modena and L. Maini, Faraday Discuss., 2022, 235, 490–507 RSC.
- H. Chung and Y. Diao, J. Mater. Chem. C, 2016, 4, 3915–3933 RSC.
- G. W. Gokel, W. M. Leevy and M. E. Weber, Chem. Rev., 2004, 104, 2723–2750 CrossRef CAS.
- S. Yu, H.-Y. Wu, V. Lemaur, C. J. Kousseff, D. Beljonne, S. Fabiano and C. B. Nielsen, Angew. Chem., 2024, 136, e202410626 CrossRef.
- H. Liao, J. Chen, L. Lan, Y. Yu, G. Zhu, J. Duan, X. Zhu, H. Dai, M. Xiao, Z. Li, W. Yue and I. McCulloch, ACS Appl. Mater. Interfaces, 2022, 14, 16477–16486 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. L. Jorgensen, M. M. Ghahremanpour, A. Saar and J. Tirado-Rives, J. Phys. Chem. B, 2024, 128, 250–262 CrossRef CAS.
- A. Landi, M. Reisjalali, J. D. Elliott, M. Matta, P. Carbone and A. Troisi, J. Mater. Chem. C, 2023, 11, 8062–8073 RSC.
- R. Alessandri, C.-H. Li, S. Keating, K. T. Mohanty, A. Peng, J. L. Lutkenhaus, S. J. Rowan, D. P. Tabor and J. J. de Pablo, JACS Au, 2024, 4, 2300–2311 CrossRef CAS.
- J. F. Coker, S. Moro, A. S. Gertsen, X. Shi, D. Pearce, M. P. van der Schelling, Y. Xu, W. Zhang, J. W. Andreasen, C. R. Snyder, L. J. Richter, M. J. Bird, I. McCulloch, G. Costantini, J. M. Frost and J. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2403879121 CrossRef PubMed.
- A. A. Y. Guilbert, M. Zbiri, P. A. Finn, M. Jenart, P. Fouquet, V. Cristiglio, B. Frick, J. Nelson and C. B. Nielsen, Chem. Mater., 2019, 31, 9635–9651 CrossRef CAS.
- S. Moro, N. Siemons, O. Drury, D. A. Warr, T. A. Moriarty, L. M. A. Perdigão, D. Pearce, M. Moser, R. K. Hallani, J. Parker, I. McCulloch, J. M. Frost, J. Nelson and G. Costantini, ACS Nano, 2022, 16, 21303–21314 CrossRef CAS PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- K.-H. Lin, L. Paterson, F. May and D. Andrienko, npj Comput. Mater., 2021, 7, 1–7 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- D. J. Cole, J. Z. Vilseck, J. Tirado-Rives, M. C. Payne and W. L. Jorgensen, J. Chem. Theory Comput., 2016, 12, 2312–2323 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- T. A. Manz and N. Gabaldon Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- N. Gabaldon Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC.
- T. A. Manz, RSC Adv., 2017, 7, 45552–45581 RSC.
- N. Gabaldon Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC.
- S. E. Root, N. E. Jackson, S. Savagatrup, G. Arya and D. J. Lipomi, Energy Environ. Sci., 2017, 10, 558–569 RSC.
- S. Sunny, S. Shah, M. Garg, I. Zozoulenko and S. Ghosh, Macromolecules, 2024, 57, 5155–5165 CrossRef CAS.
- J. Gladisch, E. Stavrinidou, S. Ghosh, A. Giovannitti, M. Moser, I. Zozoulenko, I. McCulloch and M. Berggren, Adv. Sci., 2020, 7, 1901144 CrossRef CAS.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS.
- M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105 CrossRef CAS PubMed.
- L. De Gaetani and G. Prampolini, Soft Matter, 2009, 5, 3517 RSC.
- V. Marcon, D. W. Breiby, W. Pisula, J. Dahl, J. Kirkpatrick, S. Patwardhan, F. Grozema and D. Andrienko, J. Am. Chem. Soc., 2009, 131, 11426–11432 CrossRef CAS.
- D. Andrienko, J. Mol. Liq., 2018, 267, 520–541 CrossRef CAS.
- G. R. Luckhurst and G. W. Gray, The Molecular Physics of Liquid Crystals, Academic Press, 1979 Search PubMed.
- G. V. Paolini, G. Ciccotti and M. Ferrario, Mol. Phys., 1993, 80, 297–312 CrossRef CAS.
- I. Cacelli, L. De Gaetani, G. Prampolini and A. Tani, J. Phys. Chem. B, 2007, 111, 2130–2137 CrossRef CAS.
- G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, Chem. Phys. Chem., 2009, 10, 125–136 CrossRef CAS PubMed.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- Z. Liu, S. K. M. Nalluri and J. F. Stoddart, Chem. Soc. Rev., 2017, 46, 2459–2478 RSC.
- A. Cavagna, A. Cimarelli, I. Giardina, G. Parisi, R. Santagati, F. Stefanini and M. Viale, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11865–11870 CrossRef CAS.
- D. Laage, G. Stirnemann, F. Sterpone, R. Rey and J. T. Hynes, Annu. Rev. Phys. Chem., 2011, 62, 395–416 CrossRef CAS PubMed.
- E. Duboué-Dijon and D. Laage, J. Phys. Chem. B, 2015, 119, 8406–8418 CrossRef PubMed.
- A. Cavagna, Phys. Rep., 2009, 476, 51–124 CrossRef CAS.
- S. Bonella, S. Meloni and G. Ciccotti, Eur. Phys. J. B, 2012, 85, 97 CrossRef CAS.
- CCDC 2456282: Experimental Crystal Structure Determination, 2025 DOI:10.5517/ccdc.csd.cc2nfyxz.
| This journal is © The Royal Society of Chemistry 2026 |




