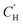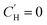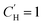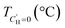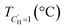Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational and experimental insights into variable temperature propylene (C3H6), propane (C3H8), and hydrogen sulfide (H2S) sorption in ultra-high permselectivity CANAL ladder polymers
Brandon C. Tapia ,
Jing Ying Yeo
,
Jing Ying Yeo and
Zachary P. Smith
and
Zachary P. Smith *
*
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: zpsmith@mit.edu
First published on 1st January 2026
Abstract
Membranes are a promising technology for energy-efficient separations of high-value gaseous chemical streams (e.g., hydrogen sulfide from methane or propane from propylene). Among the classes of emerging microporous polymers, CANAL polymers have attracted significant interest because of their selectivities and plasticization resistance for acid gas separations. In this work, a computational atomistic system is developed for CANAL-Me-Me2F, an archetypal CANAL polymer. Computed properties (free volume distribution, wide-angle X-ray scattering, and thermal expansion coefficients) align with experimental results. High-pressure sorption isotherms of H2, N2, O2, CH4, CO2, H2S, C3H6, and C3H8 were computed via grand canonical Monte Carlo and iterated Monte Carlo–molecular dynamics simulations, demonstrating good agreement with experimental isotherms at 35 °C. H2S, C3H6, and C3H8 isotherms were further computed between temperatures of 55–190 °C, followed by extraction of dual-mode sorption (DMS) parameters. Sorption energetics showed less exothermic Langmuir affinity for the more polarizable gases (H2S and C3H6) in CANAL-Me-Me2F relative to PIM-1, which is ascribed to the lack of heteroatoms in CANAL-Me-Me2F, and supported by simulations of a hypothetical nitrile-functionalized CANAL-Me-Me2F. This study develops a computational approach that can probe the unique nanoscale behavior of CANAL polymers and applies it to studying the thermodynamics of condensable gas sorption within CANAL-Me-Me2F.
1. Introduction
Reducing energy consumption in chemical separations is an important industrial target that can address up to 15% of global energy use.1 One potential route to achieving this goal is transitioning from conventional thermal-based separations to membrane-based systems, which leverage chemical potential gradients to separate compounds based upon their size and affinity to the membrane.2Ladder polymers are a promising class of emerging materials with highly rigid and contorted backbones, among which, the best known are polymers of intrinsic microporosity (PIMs).3 These materials have inefficient chain packing, yielding interconnected free volume elements that allow an increase in permeability while maintaining moderate selectivity.3 Nevertheless, the out-of-equilibrium glassy structure of PIMs results in a loss of free volume with time, decreasing their permeability that would benefit industrial application.3,4 Thus, significant work has been devoted to developing microporous membranes that can mitigate physical aging.3
In 2022, Lai et al.5 reported a class of 3D-contorted ladder polymers made via catalytic arene–norbornene annulation (CANAL) polymerization, comprised of fused norbornyl benzocyclobutene repeat units. These CANAL polymers exhibited molecular weights between 67 and 170 kDa, suitable for forming mechanically and thermally robust gas separation membranes. Interestingly, CANAL polymers exhibit a unique physical aging trend that does not follow the upper bound relationship. Instead, selectivity is greatly increased while permeability does not suffer significantly for small molecules, unlike the commonly observed tradeoff in other membrane materials, including traditional PIMs.3,6 This aging behavior allows for CANAL polymers to rival industrially used membranes in selectivity while significantly surpassing them in permeability. For example, the CANAL polymer studied in this work, CANAL-Me-Me2F, exhibits twice the selectivity and 100 times the permeability of industrial cellulose acetate membranes for CO2/CH4 separations after 150 days of aging.5
Considering these prior promising results, this study examines sorption of gas streams containing propylene (C3H6) and propane (C3H8), and hydrogen sulfide (H2S) in CANAL-Me-Me2F. These gases were selected due to their industrial relevance and the typical challenges in accessing experimental data for these gases. Propylene is an essential feedstock for plastic production, but the generation of propylene, largely via thermal cracking, also generates propane which must be removed.1,7,8 This separation is challenging due to similar boiling points (C3H6: −47.62 °C, C3H8: −42.11 °C) and van der Waals diameters (C3H6: 4.0 Å, C3H8: 4.2 Å) of the gases, leading to a highly energy-intensive distillation process.9–11 Hydrogen sulfide is another component that must be removed from hydrocarbon streams due to both its toxicity and ability to poison catalysts, especially as lower-quality feedstocks become economically feasible.12 Industrially mature fuel-gas sweetening relies on either cryogenic distillation or absorption depending on the target application (i.e., liquid or gaseous product).13,14 However, these methods must overcome enthalpies of condensation or leverage toxic solvents during operations, respectively. These unwanted features are not found in membrane separations.1,15,16
Due to the exceptional microporosity of CANAL polymers, which exhibit some of the highest BET surface areas of polymers reported in literature, they are expected to exhibit high sorption capacities despite their lack of heteroatoms.5 However, sorption studies on olefins, paraffins, and acid gases, while highly desirable, remain limited in the open literature.17,18 To the best of our knowledge, there has only been one study by Yeo et al.19 focusing on H2S separations in CANALs, and none focusing on olefin/paraffin applications. Moreover, H2S-focused studies are also limited for the archetypal PIM (PIM-1) and its derivatives.20–23 There are likely two main reasons for this lack of H2S-focused work in the literature: (1) H2S is a highly toxic gas, limiting capabilities in academic labs to consider these experiments, and (2) gathering experimental sorption data is time consuming, especially for gases such as H2S and condensable hydrocarbons with high sorption capacity. Additionally, many experimental systems are limited to temperature ranges that may be inadequate for industrial applications. Nevertheless, these studies are necessary to understand the thermodynamic behavior of these complex mixtures and to evaluate their potential in gas separations, especially as sorption selectivity can be more indicative of membrane performance relative to diffusion selectivity for highly sorbing gases, such as H2S-containing mixtures.17 Specifically, sorption analyses help to characterize polymer–gas affinity, predict effects of competitive sorption, and quantify polymer–gas energetics. As a result, these measurements are vital tools that can be used to investigate whether CANALs are a feasible materials platform for various gas separations.
Simulations provide an important complement to experiments. They can probe nanostructure relationships and conditions inaccessible to experimental methods, and can provide high throughput studies to identify promising candidates for future experimental synthesis and studies. In an effort to add to the presently limited literature on sour gas and olefin/paraffin separations in high free volume polymers, we present here a combined experimental and computational study of C3H6, C3H8, and H2S sorption within CANAL-Me-Me2F.
We validate this framework by first comparing our results to experimentally measured properties (density, wide-angle X-ray scattering, free volume distribution, and sorption isotherms), followed by simulating properties that are potentially experimentally inaccessible, namely sorption and associated energetics for C3H6, C3H8, and H2S at temperatures of 35 °C, 55 °C, 125 °C, and 190 °C.
2. Background and theory
The sorption–diffusion model is commonly applied to describe gas transport in polymeric membranes, where P is the permeability, D is the effective diffusion coefficient, and S is the effective sorption coefficient:2| P = D × S | (1) |
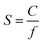 | (2) |
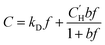 | (3) |
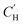 is the Langmuir capacity constant (cmSTP3 cmpol−3), and b is the Langmuir affinity constant (atm−1). The DMS model views sorption in a polymer as the simple addition of sorption in hypothetical Langmuir and Henry modes, which are said to dominate partitioning at low and high pressures, respectively.24
is the Langmuir capacity constant (cmSTP3 cmpol−3), and b is the Langmuir affinity constant (atm−1). The DMS model views sorption in a polymer as the simple addition of sorption in hypothetical Langmuir and Henry modes, which are said to dominate partitioning at low and high pressures, respectively.24
The sorption selectivity (αSi/j) for one gas over another is defined by the ratio of their respective sorption coefficients:
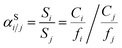 | (4) |
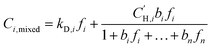 | (5) |
As there may be multiple solutions to the DMS model with similar goodness of fits as shown by Ricci et al.,28 extracting physically meaningful results from the parameters requires additional constraints within the optimization procedure. One class of constraints are linear free energy relationships (LFERs) and Van't Hoff relationships applied to the DMS fitting procedure as performed by Wu et al.29
In the limit of infinite dilution, sorption can be decoupled into Langmuir and Henry mode sorption as:
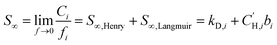 | (6) |
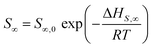 | (7) |
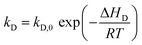 | (8) |
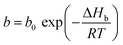 | (9) |
3. Computational methods
3.1 Simulated polymerization technique
Simulating polymer structures to extract physically meaningful property sets is challenging, primarily due to their amorphous nature and the limited chain lengths that can be accessed with simulations.33 Unlike crystalline and other ordered structures (e.g., metal–organic frameworks), amorphous polymers do not have periodic structures that can be readily compiled. Ladder polymers and PIMs bring the additional challenge of high steric hindrance due to their bulky structures.34 Thus, traditional polymer building methods such as random walks, reverse Monte Carlo (RMC), or configurational bias Monte Carlo (CBMC) methods frequently fail to properly reduce the energy of the system or reproduce experimentally observed steric hindrance.33,34 To overcome these issues, simulated polymerization was employed here using the open-source Polymatic polymerization algorithm and software (version 1.1).33,35 Briefly, the Polymatic technique places all monomers within a simulation box. Next, attempts are made to find bonding candidates based upon distance and orientation between potential bonding atoms. Should no candidates for polymerization be found, molecular dynamics are employed to search for more favorable bonding positions. Polymatic is extensively described in literature and has been validated with multiple polymers, including the archetypal microporous polymer, PIM-1.33,34,36–39The standard energy minimization strategy within the Polymatic algorithm was employed where canonical (NVT) molecular dynamics were performed every 5 polymerization steps except for when isothermal–isobaric (NPT) molecular dynamics were employed every 15 polymerization steps.33 Additional bonding orientation constraints were employed to reduce unrealistic bond generation. Artificial charges of ±0.3 e were added to bonding atoms to increase bonding probability but removed once bonding was finalized. These orientation constraints and artificial charges are built into Polymatic and have been used previously for PIM-1.33
3.2 Polymer relaxation
After polymerization, CANAL-Me-Me2F underwent a molecular dynamics relaxation scheme to more closely reflect its morphology under experimental conditions. To achieve this result, a 21-step equilibration algorithm was used where the pressure was stepped up in increments and then gradually reduced (Fig. S1 and Table S1) as recommended by Abbot et al.33 This 21-step technique was developed based on the initial work of Theodorou and Suter and modified by Larsen et al.34,40 Molecular dynamics were performed with LAMMPS (version 22 Aug 2018 for pre-processing steps and version 28 Mar 2023 for sorption isotherms).413.3 Simulation parameters
Two separate systems were developed. The first was a united-atom (UA) framework defined by the General Amber Force Field 2 (GAFF2) force field for intramolecular energies and the Transferable Potential for Phase Equilibria United-Atom (TraPPE-UA) force field for intermolecular energies as was previously shown to apply well for PIMs.33,36–38,42–48 In this UA technique, hydrogens are coupled with their respective heavy atoms, forming pseudoatoms. The second system was an all-atom (AA) framework defined by the GAFF2 force field for both inter- and intramolecular energies.45 Partial charges were generated using the restrained electrostatic potential (RESP) approach at the HF/6-31G(d) level using the Connolly surface algorithm in Gaussian 16 via the PyRed program.49–53 To quantify charges, a single repeat unit model was used, except on bonding atoms where two joined repeat units were used instead so that the charges on bonding atoms could be better described. This method of using polymer periodicity has been previously applied in charge fitting and force field parameterization as polymers are generally too large to feasibly fit quantum-mechanically-derived charges to the entire chain.42,54–56 Charge tail corrections were included up to 15 Å and cross-charges were calculated using the Lorentz–Berthelot mixing rules.57 The particle–particle–particle mesh (PPPM or P3M) method with a desired relative error (“accuracy”) of 10−5 was used to calculate long-range Coulombic interactions.58 A Nosé–Hoover thermostat and barostat59–62 were employed with Størmer–Verlet integration.63,64 All penetrants except for H2 and H2S used the GAFF2 and TraPPE-UA force fields for inter- and intramolecular parameters, respectively. The H2 force field was modeled using the parameters of Yang and Zhong,65 as suggested for use by Barraco et al.66 The H2S force field was modeled using a modified 4–3 model originally developed by Shah et al.67 Additional information on the H2S force field is available in Section S1.3 of the SI.3.4 Fixed and flexible adsorption techniques
Grand canonical Monte Carlo (GCMC) simulations were employed to generate sorption isotherms using the Cassandra Monte Carlo package (version 1.2.6).68 GCMC holds chemical potential (µ), volume (V), and temperature (T) constant. Both a rigid and a flexible method were employed for sorption isotherm generation. The rigid method solely employed GCMC with the polymer system held static throughout the run. These rigid simulations were run for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps with the final one-third of the data used to calculate equilibrium averages (Fig. S3). The flexible method employed iterative MC and MD (MCMD), where one iteration consisted of 2
000 MC steps with the final one-third of the data used to calculate equilibrium averages (Fig. S3). The flexible method employed iterative MC and MD (MCMD), where one iteration consisted of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps followed by 2 ns of isothermal–isobaric MD with a 0.5 fs timestep to allow for system relaxation. All inserted gas molecules were intramolecularly fixed (i.e., no bending or stretching) but were allowed to rotate and translate during MD. The 0.5 fs timestep was used to account for this rigid adsorbate assumption as reported previously.37 Each flexible isotherm was run for at least 5 cycles at each pressure point, but cycles were continued until they converged (Fig. S4 and S5 and Table S2). To achieve these flexible simulations, communication between LAMMPS and Cassandra was performed with the Python-based pysimm package (using an in-house modified distribution of version 1.1, both of which are open-source).69–73 The flexible method provides a more realistic system description of condensable gas uptake by allowing molecular rearrangement, but it is significantly more computationally expensive than the rigid method.
000 MC steps followed by 2 ns of isothermal–isobaric MD with a 0.5 fs timestep to allow for system relaxation. All inserted gas molecules were intramolecularly fixed (i.e., no bending or stretching) but were allowed to rotate and translate during MD. The 0.5 fs timestep was used to account for this rigid adsorbate assumption as reported previously.37 Each flexible isotherm was run for at least 5 cycles at each pressure point, but cycles were continued until they converged (Fig. S4 and S5 and Table S2). To achieve these flexible simulations, communication between LAMMPS and Cassandra was performed with the Python-based pysimm package (using an in-house modified distribution of version 1.1, both of which are open-source).69–73 The flexible method provides a more realistic system description of condensable gas uptake by allowing molecular rearrangement, but it is significantly more computationally expensive than the rigid method.
3.5 Uncertainty and error propagation
As CANAL-Me-Me2F is amorphous, five different systems were generated independently using Polymatic. Uncertainties in “static” properties (i.e., properties that were directly calculated from the equilibrated polymer system, e.g., density) were determined as the sample standard deviation between the five replicates. Uncertainties in Monte Carlo simulations were determined as the sample standard deviation of the fluctuations within each replicate's equilibrium value, followed by error propagation between the five replicates.743.6 Gravimetric and volumetric sorption
Depending on the study, results may be reported gravimetrically (e.g., mmol g−1) or volumetrically (e.g., cmSTP3 cmpol−3) where conversion between the two is described as follows:
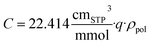 | (10) |
While both methods are reasonable, challenges arise when attempting to compare computationalto experimental results. Since the polymer density within the simulation may not match that of experiment, as has been previously shown by Abott et al.33 for PIM-1, the conversion between measurement styles can influence comparison between simulated and experimental results. To account for this density difference, the simulated volumetric results reported here are scaled by the ratio of experimental to simulated densities, effectively normalizing the results so that they are comparable regardless of measurement style reported. In other words, the ρpol used in eqn (10) is the experimental density, not the simulated density.
4. Experimental methods
4.1 Density measurements
CANAL-Me-Me2F films were solution cast and subject to methanol treatment using the same procedure described in Lai et al.5 The density of the films was measured using a gravimetric approach, and the area was determined using a hand-traced polygon in ImageJ software (version 1.51 k).76 The thickness across the films was measured using a Mituyo (Kanagawa, Japan) micrometer, with an accuracy of ± 1.27 µm.4.2 Free volume distribution via non-local density functional theory (NLDFT)
BET surface areas of the CANAL-Me-Me2F polymers were measured with an N2 probe at 77 K using a Micromeritics ASAP 2020 with the same procedure as described in Lai et al.5 Analysis of free volume distributions was performed using the non-local density functional theory (NLDFT) model for carbon slit pore geometry using the SAIEUS software, which implements the L-curve method for the regularization parameter, λ.774.3 Experimental gas sorption isotherm measurements
Gas sorption isotherms for the CANAL-Me-Me2F films were collected using an automated constant-volume pressure-decay system from Maxwell Robotics (Austin, TX) at 35 °C. A detailed protocol for these tests can be found in previous work by Mizrahi Rodriguez et al.784.4 Thermal expansion coefficient via dynamic mechanical analysis (DMA)
To understand the dimensional change in the CANAL-Me-Me2F films during heating, the length of each film was continuously measured using a single screw film clamp test experiment on a TA Instruments (New Castle, DE) DMA 850 using a heating (30 to 140 °C) procedure with a ramp rate of 5 °C min−1.4.5 Materials
Chloroform (HPLC grade) and methanol (ACS reagent grade) were purchased from Sigma Aldrich (St. Louis, MO). The following gases were purchased from Airgas (Radnor, PA): He (>99.999%), H2 (>99.999%), N2 (>99.999%), O2 (>99.999%), CH4 (>99.99%), H2S (air certified standard mixture, 99.99%), C3H6 (>99.0%), and C3H8 (>99.0%). CANAL-Me-Me2F polymer used for C3H8 and C3H6 sorption and density measurements was purchased from Osmoses (Cambridge, MA). CANAL-Me-Me2F polymer used for H2, O2, N2, and CH4 sorption is the same polymer as previously studied by Lai et al.55. Results and discussion
5.1 System validation
The chosen molecular system parameters were validated via structural property alignment between simulated and experimental systems. To make this validation, bulk density, skeletal density, free volume distribution (FVD), and the static structure factor of the simulated system were determined.Bulk density is defined as
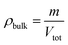 | (11) |
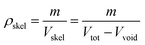 | (12) |
The experimental bulk density at room temperature of 0.96 ± 0.02 g cm−3 led to differences of 17% and 1% compared to the bulk densities of the UA and AA frameworks at 35 °C, respectively. Abbot et al.35 reported simulated bulk densities for UA frameworks consistently lower than experimental bulk densities for multiple polymers (PS, PMMA, PET, PC, PEI, PIM-1) when polymerized with Polymatic, hypothetically due to difficulty in comparing geometrically- and experimentally-derived densities, especially for high free volume polymers, where differences are likely amplified.
The simulated bulk density of the polymer decreases with increasing temperature for both the UA and AA frameworks as shown in Fig. 1. Interestingly, the slopes of the density versus temperature plots for both the UA and AA frameworks are remarkably similar at (−2.2 ± 0.2)·10−4 g cm−3 K−1 and (−2.3 ± 0.2)·10−4 g cm−3 K−1, respectively for bulk density. Free volume theory predicts that an increase in free volume should increase the volumetric thermal expansion coefficient, αV, defined as:81
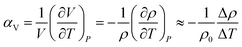 | (13) |
The experimental volumetric thermal expansion coefficient was determined from the linear thermal expansion coefficient (αL) and, assuming isotropic expansion, calculated as:89
| αV = 3αL | (14) |
| System | Polymer | αV (104·K−1) | Temperature range (°C) |
|---|---|---|---|
| a As further explained in Section S2.1, the experimental αV was found using a polynomial fit, creating a non-constant value.b Reference provided αV, thus, eqn (14) was not applied. | |||
| United-atom | CANAL-Me-Me2F | 2.2 ± 0.8 | 35–150 |
| 2.7 ± 0.3 | 15–300 | ||
| All-atom | CANAL-Me-Me2F | 2.3 ± 0.6 | 35–150 |
| 2.4 ± 0.2 | 15–300 | ||
| Experimental | CANAL-Me-Me2F | 1.0–2.2a | 35–139 |
| Experimental90 | Polystyrene | 1.8–2.4 | <Tg |
| Experimental90 | poly(methyl methacrylate) | 2.1 | <Tg |
| Experimental91 | Cellulose acetate | 3.3b | <Tg |
| Experimental92 | PIM-1 | 2.1 | 30–110 |
To better understand the polymer microstructure, the FVD was calculated using PoreBlazer, defined as the negative derivative of the cumulative free volume, V, with respect to the probe diameter, D:
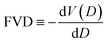 | (15) |
Fig. 2b and c detail the minimum and maximum pore sizes present, taken as the values at which 99% and 1% of the cumulative free volume was accessible, respectively, over a 15–300 °C temperature range. The AA framework shows a narrower FVD than the UA framework across all temperatures. The FVD is seen to broaden with increasing temperature—largely due to the increase in the maximum FVE size, which increases an order of magnitude faster than the minimum FVE size. These results agree with the density decreasing as a function of temperature, as free volume elements may increase in size as the polymer expands. The more uniform minimum FVE size with increasing temperature suggests that even though the average FVE size may increase, there remain stochastically fluctuating pockets that maintain gas sieving capabilities even at high temperatures.
Crystallographic data was computed using the Interactive Structure Analysis of Amorphous and Crystalline Systems (ISAACS) program (version 2.10).97 The static structure factor, S(q), was used to compare against experimental wide-angle X-ray scattering (WAXS) data from Lai et al.5 The simulated scattering data reasonably follows the experimentally gathered data with a broad amorphous halo around 1.0 Å−1 as shown in Fig. 3. The d-spacing for the amorphous halo of the experimental results is 7.1 Å, while that of the UA and AA results are 6.6 Å and 6.5 Å, respectively. For the experimental result, the increase in intensity as q goes to zero is not visible in the simulated static structure factor and is attributed to experimental error as the regime around and below 0.3 Å−1 is better suited for small-angle X-ray scattering (SAXS).98
 | ||
| Fig. 3 Experimental wide-angle X-ray scattering (WAXS) data (solid line) from Lai et al.5 compared with simulated static structure factors of all-atom (dotted line) and united-atom (dashed line) CANAL-Me-Me2F systems. Error bands represent the sample standard deviation from five replicate polymer systems. Data are normalized to their maximum ordinate value in the range 0.9–1.1 Å−1. | ||
5.2 Small-gas sorption isotherms
This study focuses primarily on H2S, C3H6, and C3H8, which are plasticizing gases. When compared to smaller gases, such as H2 and N2, these larger gases create complexities with modeling, such as the need for additional force field parameters and iterated MCMD. To better understand limitations specific to the polymer model itself, sorption isotherms for fixed-framework UA models of H2, N2, O2, and CH4 were simulated at 35 °C and compared to experimentally obtained sorption isotherms, shown in Fig. 4. Because these smaller gases do not cause detectable polymer plasticization, flexible frameworks do not provide increased convergence with experimental results, as shown explicitly in Fig. 4a and d for H2 and CH4, respectively. | ||
| Fig. 4 Comparisons of united-atom simulations and experimental (black squares) isotherms in CANAL-Me-Me2F for (a) H2, (b) N2, (c) O2, and (d) CH4, all at 35 °C. Rigid (filled datapoints) and flexible (unfilled datapoints) isotherms were computed for H2 and CH4 while only rigid isotherms were computed for N2 and O2. Fugacity was calculated via a second-order Virial expansion.99 | ||
The simulated systems show quantitative agreement with experimental results. Specifically, results for H2, N2, and O2 fall within error of experimental values, while results for CH4 show slight under- or overprediction depending on whether an MC or MCMD procedure was applied. The usage of a flexible framework increases the sorbed concentration of a gas when compared to the rigid framework, as polymer rearrangement within the flexible framework allows gas molecules to settle in previously inaccessible locations. These results indicate the ability for the CANAL-Me-Me2F model to quantitatively model sorption using GCMC for non-plasticizing gases and give credence to the relevance of the chosen forcefield parameters. The ability to model experimental isotherms agrees with previous studies that have found GCMC to be a valuable tool for predicting sorption of non-plasticizing gases in polyimides, porous aromatic frameworks, and PIMs.34,100,101
5.3 Plasticizing gas sorption isotherms
For plasticizing gases (e.g., CO2, H2S, C3H6, and C3H8), the effects of fixed versus flexible framework were significant, as exemplified in Fig. 5. For CO2, the flexible framework overpredicted yet showed qualitative agreement with experimental results at fugacities below 20 atm before strongly diverging. Interestingly, for CO2, the flexible framework performed worse than the fixed framework. The flexible framework model for H2S underpredicted yet qualitatively aligned with the experimental H2S isotherm at fugacities below 10 atm. For the larger C3H6 and C3H8 hydrocarbons, quantitative agreement with experimental isotherms is demonstrated at low to moderate fugacities (<3 atm), indicating the applicability of this flexible framework. These comparisons with experimental results highlight how the polar molecules (CO2 and H2S) show poorer alignment with experimental results than the hydrocarbons. This result could be due to the additional force field complexities that arise for interparticle interactions when significant polarity is present, amplifying the relative simplicity of force fields compared to actual molecular electronic behavior. Therefore, even for plasticizing gases, it is advisable to compare both fixed and flexible frameworks to determine which is best for specific cases. | ||
| Fig. 5 Comparison of flexible framework united-atom simulations and experimental isotherms in CANAL-Me-Me2F at 35 °C for (a) CO2, (b) H2S, (c) C3H6, and (d) C3H8. Experimental results are shown with black squares while flexible framework (MCMD) simulations are shown with colored circles. Fixed framework united-atom simulations are shown for CO2 in (a) as triangles. Fugacity was determined for CO2, C3H6 and C3H8 via a second-order Virial expansion and for H2S with the Peng–Robinson equation of state.99,102,103 The experimental H2S isotherm has previously been reported in Yeo et al.19 | ||
Previous studies that have examined CO2 sorption in PIM-1 using the iterative MCMD approach have reported both under- and overfitting, compared to experimental results.37,104 The broad range of CO2 sorption isotherms in PIM-1 is indicative of the fact that slight changes in reaction conditions, post-treatment, and testing methods can significantly alter the results.105 Compounding these challenges is the issue that simulated “synthesis,” relaxation, and sorption measurements are unable to be performed as one would do experimentally. Thus, we emphasize that divergence from experimental results is not unexpected given these limitations and experimental scatter.106
5.4 Dual-mode sorption model
An LFER and Van't Hoff constrained DMS model has previously been applied to CANALs and H2S sorption in glassy polymers.19,22 Here, we extend those H2S results reported at 35 °C to 35–190 °C. Sorption isotherms and their corresponding DMS fits are shown in Fig. 6 with DMS parameters tabulated in Table 2. As the effect of Langmuir sorption decreases with increasing temperature due to the deactivation of surface modes and the exothermic nature of Langmuir sorption, the sorption isotherms become more linear with increasing temperature. Details on the DMS fitting procedure including initial guesses and parameter bounds (Tables S4–5) are available in the SI. | ||
| Fig. 6 Simulated MCMD sorption isotherms and corresponding dual-mode sorption (DMS) model fits for (a) H2S, (b) C3H6, and (c) C3H8 at temperatures of 35 °C, 55 °C, 125 °C, and 190 °C. DMS fits were restricted via linear-free energy relationships (LFERs) and Van't Hoff constraints as implemented by Wu et al.29 Uncertainties in DMS parameters were estimated from the inverse of the Hessian of χ2 at the optimum, followed by standard error propagation to determine uncertainty in concentration.74 | ||
| Gas | Temperature (°C) | kD (cmSTP3 cmpol−3 atm−1) | (cmSTP3 cmpol−3) | b (atm−1) |
|---|---|---|---|---|
| H2S | 35 | 13.7 ± 0.2 | 87 ± 3 | 0.223 ± 0.002 |
| 55 | 9.9 ± 0.1 | 54 ± 2 | 0.210 ± 0.005 | |
| 125 | 4.12 ± 0.03 | 8 ± 2 | 0.18 ± 0.02 | |
| 190 | 2.32 ± 0.01 | 0.0 ± 0.5 | 0.16 ± 0.03 | |
| C3H6 | 35 | 13.5 ± 0.2 | 53 ± 1 | 2.40 ± 0.04 |
| 55 | 10.4 ± 0.1 | 40.5 ± 0.4 | 1.60 ± 0.01 | |
| 125 | 5.2 ± 0.1 | 12 ± 1 | 0.54 ± 0.03 | |
| 190 | 3.3 ± 0.1 | 0.0 ± 0.7 | 0.26 ± 0.02 | |
| C3H8 | 35 | 10.2 ± 0.2 | 61 ± 1 | 2.64 ± 0.05 |
| 55 | 8.4 ± 0.1 | 51.7 ± 0.6 | 1.58 ± 0.01 | |
| 125 | 5.0 ± 0.1 | 20 ± 1 | 0.39 ± 0.01 | |
| 190 | 3.5 ± 0.1 | 0 ± 1 | 0.16 ± 0.01 |
In the optimization, no functional form was fit to the Langmuir capacity constant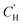 , as it has previously been fit to both linear107 and Van't Hoff temperature dependent models,32 as shown in eqn (16) and (17), respectively:
, as it has previously been fit to both linear107 and Van't Hoff temperature dependent models,32 as shown in eqn (16) and (17), respectively:
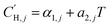 | (16) |
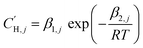 | (17) |
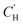 parameter from the LFER-constrained DMS model across a large range of temperatures. As shown in Fig. 7, both models show similar goodness-of-fit. The log-modified mean absolute percentage error (MAPE)108 for each model is shown in Table 3, indicating that the more applicable model in a given scenario is dependent on the specified gas and temperature. However, when extrapolating towards
parameter from the LFER-constrained DMS model across a large range of temperatures. As shown in Fig. 7, both models show similar goodness-of-fit. The log-modified mean absolute percentage error (MAPE)108 for each model is shown in Table 3, indicating that the more applicable model in a given scenario is dependent on the specified gas and temperature. However, when extrapolating towards 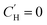 to approximate where Langmuir sorption is no longer present, the proposed Van't Hoff relationship significantly overpredicts the corresponding temperatures compared to the linear fit. The linear fits predict there to be a loss of Langmuir sorption between 132–167 °C, as is reflected in the sorption isotherms of Fig. 6 where the sorption isotherms at 190 °C exhibit negligible Langmuir contribution. As the Van't Hoff relationship does not allow for determination at
to approximate where Langmuir sorption is no longer present, the proposed Van't Hoff relationship significantly overpredicts the corresponding temperatures compared to the linear fit. The linear fits predict there to be a loss of Langmuir sorption between 132–167 °C, as is reflected in the sorption isotherms of Fig. 6 where the sorption isotherms at 190 °C exhibit negligible Langmuir contribution. As the Van't Hoff relationship does not allow for determination at  , results are reported for
, results are reported for  . This Van't Hoff fit does not predict loss of Langmuir sorption until between 262–1279 °C. This broad range illustrates the limitations of using phenomenological models for material property predictions and corroborates conclusions by Koros and Paul107 and Koros et al.32 who determined that while the Van't Hoff fit is “convenient,” it lacks theoretical justification. The linear fit, they argued, can be better related to the free volume within the polymer below its glass transition temperature and subsequent vanishing at the glass transition temperature. A comprehensive study of Xe sorption and 129Xe NMR using poly(p-phenylene oxide) supported the observation that a linear extrapolation of
. This Van't Hoff fit does not predict loss of Langmuir sorption until between 262–1279 °C. This broad range illustrates the limitations of using phenomenological models for material property predictions and corroborates conclusions by Koros and Paul107 and Koros et al.32 who determined that while the Van't Hoff fit is “convenient,” it lacks theoretical justification. The linear fit, they argued, can be better related to the free volume within the polymer below its glass transition temperature and subsequent vanishing at the glass transition temperature. A comprehensive study of Xe sorption and 129Xe NMR using poly(p-phenylene oxide) supported the observation that a linear extrapolation of 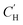 to zero corroborates well with the location of the Tg, where
to zero corroborates well with the location of the Tg, where 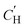 is expected to become negligible.109 However, extrapolations in this work do not identify a clear Tg that can be identified experimentally, as CANAL polymers do not have a detectable Tg prior to thermal degradation at ∼450 °C.5
is expected to become negligible.109 However, extrapolations in this work do not identify a clear Tg that can be identified experimentally, as CANAL polymers do not have a detectable Tg prior to thermal degradation at ∼450 °C.5
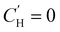 for linear and
for linear and 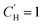 for Van't Hoff fits of
for Van't Hoff fits of 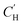 versus temperature and inverse temperature, respectively
versus temperature and inverse temperature, respectively
5.5 Sorption energetics
To better understand polymer–gas affinity between CANAL-Me-Me2F and C3H6, C3H8, and H2S, as well as to understand how these results differ from the archetypal microporous polymer, PIM-1, the thermodynamics of sorption were analyzed via the DMS model. The same LFER-constrained model as detailed above for CANAL-Me-Me2F was used for PIM-1. The DMS parameters for H2S in PIM-1 were computed from the isotherms of Dean et al.22 The DMS parameters for C3H6 and C3H8 in PIM-1 were computed from the isotherms of Li et al.110 These parameters are reported in Table S7. We note that when using an unconstrained DMS optimization, sorption energetics in PIM-1 can lead to significantly different values and trends (Table S9), thus, efforts to constrain parameters to physically-relevant trends are vital to more reliable structure–property relationships.Langmuir sorption, as shown in Fig. 8a and Table S6, is responsible for over 55% of infinite dilution sorption at 35 °C for H2S and over 90% for the two hydrocarbons. By 125 °C, however, these values decrease to between 25% and 65%, indicating the stronger temperature dependence of Langmuir sorption compared to Henry sorption. As shown in Fig. 8b, the sorption coefficient at infinite dilution, S∞, of H2S in PIM-1 has a larger contribution from the Langmuir mode than CANAL-Me-Me2F. This result correlates with the lower plasticization pressure of CANALs.19 The significantly lower S∞ for H2S in CANAL-Me-Me2F was expected due to the degree of linearity exhibited in the isotherms shown in Fig. 6a.
 | ||
| Fig. 8 (a) Sorption coefficient at infinite dilution (S∞) for H2S, C3H6, and C3H8 in CANAL-Me-Me2F at temperatures of 35 °C, 55 °C, 125 °C, and 190 °C. Uncertainty is propagated from uncertainty in the DMS parameters and shown as the combined uncertainty of both Langmuir and Henry modes. (b) Percent contribution of S∞ from the Langmuir mode for CANAL-Me-Me2F and PIM-1, compared for H2S, C3H6 and C3H8 at 35 °C. PIM-1 parameters were fit using previously published isotherms.22,110 | ||
As detailed explicitly in Table 4, the trends in heats of sorption differ between CANAL-Me-Me2F and PIM-1. Analysis of the energetics of infinite dilution sorption for the two hydrocarbons showed that in PIM-1, C3H6 was significantly more exothermic than C3H8 (ΔHS,∞,C3H6 − ΔHS,∞,C3H8 ≈ −20 kJ mol−1) while in CANAL-Me-Me2F, the two terms were nearly within uncertainty of each other (≈ 1 kJ mol−1). These differences in energetics between the two hydrocarbons are most significantly due to partitioning within the Langmuir regime, as differences in ΔHD between C3H6 and C3H8 were within 3 kJ mol−1 for both polymers.
| Polymer | Gas | ΔHS,∞ (kJ mol−1) | ΔHD (kJ mol−1) | ΔHb (kJ mol−1) |
|---|---|---|---|---|
| CANAL-Me-Me2F | H2S | −20.5 ± 0.2 | −13.6 ± 0.1 | −2 ± 1 |
| C3H6 | −29.0 ± 0.3 | −10.9 ± 0.3 | −17.0 ± 0.8 | |
| C3H8 | −30.0 ± 0.3 | −8.2 ± 0.4 | −21.7 ± 0.6 | |
| PIM-1 | H2S | −27.2 ± 0.2 | −17.0 ± 0.3 | −23.2 ± 0.2 |
| C3H6 | −37.9 ± 0.7 | −22.1 ± 0.1 | −33.5 ± 0.3 | |
| C3H8 | −18.0 ± 0.7 | −22.0 ± 0.6 | −12.2 ± 0.6 |
The differences seen in the energetics of surface sorption of C3H6 and C3H8 between CANAL-Me-Me2F and PIM-1 are hypothesized to be due to the heteroatoms within PIM-1 that are not present in CANAL-Me-Me2F. Propylene is more polarizable than propane, leading to potentially stronger interactions between the nitrile functionality in PIM-1 and the π-bond in propylene.111 While no other studies on propylene sorption in CANALs have been performed, this effect can be likened to how increased side group polarity in PIM-1 (e.g., conversion of nitrile groups to primary amines), increases the sorption selectivity of propylene over propane.112 To further support the polarizability hypothesis, sorption simulations as described previously were conducted on a hypothetical CANAL-Me-Me2F-like polymer with two methyl groups per repeat unit substituted for nitrile groups (CANAL-Me-Me2F-CN), as shown in Fig. 9. As shown in Fig. 10, the Langmuir energetics of propylene were made more exothermic relative to propane while the Henry energetics remained similar. Details on the computational modeling of CANAL-Me-Me2F-CN are available in Section S1.5 and DMS parameters are available in Table S8.
 | ||
| Fig. 9 Structures of CANAL-Me-Me2F, CANAL-Me-Me2F-CN, and PIM-1. Note that the CANAL-Me-Me2F-CN structure is hypothetical. | ||
 | ||
| Fig. 10 Difference in heats of sorption between CANAL-Me-Me2F-CN (ΔHCN) and CANAL-Me-Me2F (ΔH) for infinite dilution, Henry, and Langmuir sorption from constrained DMS optimization routines. | ||
Similar to the previously described differences in Langmuir sorption of C3H6 in CANAL-Me-Me2F and PIM-1, H2S, as a polar molecule, demonstrates more exothermic Langmuir sorption in PIM-1 (ΔHb ≈ −23 kJ mol−1) than in CANAL-Me-Me2F (≈ −2 kJ mol−1). As also shown in Fig. 10, the Langmuir energetics of H2S are more exothermic in CANAL-Me-Me2F-CN than in CANAL-Me-Me2F. Due to overlapping uncertainties between these energetic differences in H2S and non-polar C3H8, however, these results are less conclusive than those of C3H6 described above.
Interestingly, ΔHD values for all three gases in CANAL-Me-Me2F are less exothermic than those obtained for the same gases in PIM-1. This result aligns with a previous finding that differences in sorption in the Henry's mode were strongly influenced by polymer backbone and less so on specific functionality.22 In further agreement is that ΔHD values between CANAL-Me-Me2F and CANAL-Me-Me2F-CN are within uncertainties of each other.
5.6 Mixed-gas sorption
To investigate the ability for CANAL-Me-Me2F to perform the industrially relevant propylene/propane separation, the mixed-gas DMS model was applied. A 70/30 molar ratio of propylene/propane was chosen as a balance between typical hydrocarbon stream composition from catalytic cracking (>80 mol% propylene) and from propane dehydrogenation (50 mol% propylene).113,114The effect of the mixed-gas DMS model on the sorption isotherms of C3H6 and C3H8 at 35 °C is shown in Fig. 11a, yielding the characteristic decrease in Langmuir capacity with unchanged sorption effects of the Henry mode, as expected from the mixed-gas model formulation. The mixed-gas selectivities in CANAL-Me-Me2F (αSC3H6/C3H8 = SC3H6/SC3H8) are shown in Fig. 11b. Due to significant uncertainties in the selectivities, the effect of increasing temperature on selectivity from 35 °C to 190 °C cannot be definitively stated.
 | ||
| Fig. 11 (a) Dual-mode sorption (DMS) isotherms for C3H6 and C3H8 in CANAL-Me-Me2F for pure-gas (solid lines) and mixed-gas (dashed lines) for a 70/30 molar mixture of C3H6/C3H8 at 35 °C versus the fugacity of each component. DMS fits were restricted via linear-free energy relationships (LFERs) as implemented by Wu et al.29 (b) Mixed-gas sorption selectivity of a 70/30 molar mixture of C3H6/C3H8 in CANAL-Me-Me2F at 35 °C and 190 °C versus the combined fugacity of both penetrants. (c) Mixed-gas sorption selectivity of a 70/30 molar mixture of C3H6/C3H8 in CANAL-Me-Me2F and PIM-1 at 35 °C versus the combined fugacity of both penetrants. Data for CANAL-Me-Me2F is from simulated MCMD isotherms. Data for PIM-1 is from the recomputed isotherms of Li et al.110 | ||
Comparison of the propylene/propane sorption selectivity between CANAL-Me-Me2F and PIM-1 at 35 °C is shown in Fig. 11c. CANAL-Me-Me2F has a sorption selectivity below one for the majority of the fugacity range studied, while PIM-1 has a sorption selectivity near one. As the Langmuir mode becomes saturated with increasing fugacity, the potential surface sorption differences between the two polymers as examined previously decrease in importance, and the propylene/propane selectivities in CANAL-Me-Me2F and PIM-1 trend towards each other.
6. Conclusions
This study establishes an atomistic computational framework for CANAL polymers, which was validated against experimental data including density, free volume distribution (FVD), wide-angle X-ray scattering (WAXS), and sorption isotherms. Furthermore, a significant focus was placed on simulating the sorption and corresponding energetics of H2S, C3H6, and C3H8, which are difficult to evaluate experimentally. While non-plasticizing gases were quantitatively modeled via GCMC, highly condensable gases—particularly the C3H6 and C3H8 hydrocarbons—required an iterative MCMD approach. These results support the use of MCMD simulations as a predictive tool, especially for time-intensive sorption studies and those with hazardous gases. Application of the dual-mode sorption (DMS) model over a broad range of temperatures from 35 °C to 190 °C for H2S, C3H6, and C3H8 within CANAL-Me-Me2F revealed the significant characteristic Langmuir-mode contribution to sorption at lower temperatures and pressures. By 190 °C, sorption isotherms were nearly linear and characterized by the Henry mode. The higher Langmuir affinities for the hydrocarbons relative to H2S in the purely hydrocarbon CANAL emphasizes how sorption in the CANAL polymer is largely driven by van der Waals interactions. Langmuir energetics were more exothermic for H2S and C3H6 in PIM-1 than in CANAL-Me-Me2F, potentially due to specific gas–polymer interactions made feasible through the nitrile group present in PIM-1, which was supported by simulations of a hypothetical nitrile-functionalized CANAL-Me-Me2F. Overall, this work advances the understanding of condensable gas sorption in high free volume heteroatom-free ladder polymers. The microstructural and multi-temperature sorption analyses performed within this study suggest that increasing size-sieving through CANAL backbone modification can be quantified via geometric FVDs, aromaticity can be leveraged to favor Langmuir sorption of polarizable penetrants, and temperature can be used to significantly modulate the contribution of Langmuir sorption within CANALs. By validating an atomistic simulation system for CANAL-Me-Me2F, we provide a foundation for extending computational studies to other CANAL polymers. When used in conjunction with experiments, these simulations enable a more complete characterization of sorption behavior and support the rational design of membrane materials for complex gas separations.Author contributions
B. C. Tapia: conceptualization, methodology, software, formal analysis, investigation, data curation, writing – original draft, visualization. J. Y. Yeo: conceptualization, methodology, formal analysis, investigation, writing – review & editing. Z. P. Smith: supervision, writing – review & editing, funding acquisition.Conflicts of interest
Zachary P. Smith reports a relationship with Osmoses, Inc. that includes: board membership, consulting or advisory, and equity or stocks. Zachary P. Smith has patent licensed to Osmoses., Inc.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ta09448h.Acknowledgements
The authors thank Pablo A. Dean for helpful discussions on the DMS model optimization, Cassiano G. Aimoli for helpful discussions on molecular simulations, Francesco M. Benedetti for sorption experiments of H2, N2, O2, CH4, and CO2, and Ashley M. Robinson and Yan Xia for helpful discussions on CANAL polymer synthesis. The authors acknowledge the MIT SuperCloud, the Lincoln Laboratory Supercomputing Center, and the MIT Office of Research Computing and Data for providing HPC resources that have contributed to the research results reported within this paper. This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Separation Science Program under Award DE-SC0023252.References
- D. S. Sholl and R. P. Lively, Seven chemical separations to change the world, Nature, 2016, 532(7600), 435–437, DOI:10.1038/532435a.
- J. G. Wijmans and R. W. Baker, The solution-diffusion model: A review, J. Membr. Sci., 1995, 107(1), 1–21, DOI:10.1016/0376-7388(95)00102-i.
- Z.-X. Low, P. M. Budd, N. B. McKeown and D. A. Patterson, Gas permeation properties, physical aging, and its mitigation in high free volume glassy polymers, Chem. Rev., 2018, 118(12), 5871–5911, DOI:10.1021/acs.chemrev.7b00629.
- A. G. McDermott, P. M. Budd, N. B. McKeown, C. M. Colina and J. Runt, Physical aging of polymers of intrinsic microporosity: a SAXS/WAXS study, J. Mater. Chem. A, 2014, 2(30), 11742–11752, 10.1039/c4ta02165g.
- H. W. H. Lai, F. M. Benedetti, J. M. Ahn, A. M. Robinson, Y. Wang, I. Pinnau, Z. P. Smith and Y. Xia, Hydrocarbon ladder polymers with ultrahigh permselectivity for membrane gas separations, Science, 2022, 375(6587), 1390–1392, DOI:10.1126/science.abl7163.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Maximizing the right stuff: The trade-off between membrane permeability and selectivity, Science, 2017, 356(6343), eaab0530, DOI:10.1126/science.aab0530.
- L.-P. Guo, R.-S. Liu, J. Qian, G.-P. Hao, J. Guo, H. Wu, F. Wang and A.-H. Lu, Surface sieving carbon skins for propylene and propane separation, Nat. Chem. Eng., 2024, 1(6), 411–420, DOI:10.1038/s44286-024-00075-9.
- C. C. E. Christopher, A. Dutta, S. Farooq and I. A. Karimi, Process synthesis and optimization of propylene/propane separation using vapor recompression and self-heat recuperation, Ind. Eng. Chem. Res., 2017, 56(49), 14557–14564, DOI:10.1021/acs.iecr.7b03432.
- Physical constants of organic compounds, in CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press/Taylor & Francis, Boca Raton, FL, 106th edn, 2025 Search PubMed.
- C. Zhang, R. P. Lively, K. Zhang, J. R. Johnson, O. Karvan and W. J. Koros, Unexpected molecular sieving properties of Zeolitic Imidazolate Framework-8, J. Phys. Chem. Lett., 2012, 3(16), 2130–2134, DOI:10.1021/jz300855a.
- Y. Su, S. Cong, M. Shan and Y. Zhang, Enhanced propylene/propane separation in facilitated transport membranes containing multisilver complex, AIChE J., 2022, 68(1), e17410, DOI:10.1002/aic.17410.
- Y. H. Chan, S. S. M. Lock, M. K. Wong, C. L. Yiin, A. C. M. Loy, K. W. Cheah, S. Y. W. Chai, C. Li, B. S. How, B. L. F. Chin, Z. P. Chan and S. S. Lam, A state-of-the-art review on capture and separation of hazardous hydrogen sulfide (H2S): Recent advances, challenges and outlook, Environ. Pollut., 2022, 314, 120219, DOI:10.1016/j.envpol.2022.120219.
- A. Pudi, M. Rezaei, V. Signorini, M. P. Andersson, M. G. Baschetti and S. S. Mansouri, Hydrogen sulfide capture and removal technologies: A comprehensive review of recent developments and emerging trends, Sep. Purif. Technol., 2022, 298, 121448, DOI:10.1016/j.seppur.2022.121448.
- T. N. A. Tengku Hassan, A. M. Shariff, M. M. Mohd Pauzi, M. S. Khidzir and A. Surmi, Insights on cryogenic distillation technology for simultaneous CO2 and H2S removal for sour gas fields, Molecules, 2022, 27(4), 1424, DOI:10.3390/molecules27041424.
- F. B. Torres, J. P. Gutierrez, L. A. Ruiz, M. A. Bertuzzi and E. Erdmann, Comparative analysis of absorption, membrane, and hybrid technologies for CO2 recovery, J. Nat. Gas Sci. Eng., 2021, 94, 104082, DOI:10.1016/j.jngse.2021.104082.
- X. He, D. Chen, Z. Liang and F. Yang, Insight and comparison of energy-efficient membrane processes for CO2 capture from flue gases in power plant and energy-intensive industry, Carbon Capture Sci. Technol., 2022, 2, 100020, DOI:10.1016/j.ccst.2021.100020.
- K. Mizrahi Rodriguez, S. Lin, A. X. Wu, K. R. Storme, T. Joo, A. F. Grosz, N. Roy, D. Syar, F. M. Benedetti and Z. P. Smith, Penetrant-induced plasticization in microporous polymer membranes, Chem. Soc. Rev., 2024, 53(5), 2435–2529, 10.1039/d3cs00235g.
- D. S. Sholl and R. P. Lively, Exemplar mixtures for studying complex mixture effects in practical chemical separations, JACS Au, 2022, 2(2), 322–327, DOI:10.1021/jacsau.1c00490.
- J. Y. Yeo, F. M. Benedetti, B. Pedretti, A. M. Robinson, R. Yin, H. W. H. Lai, T. H. Lee, Y. Xia and Z. P. Smith, Investigation of competitive sorption and plasticization of hyperaged CANAL ladder polymers for acid gas purification, J. Membr. Sci., 2025, 726, 123973, DOI:10.1016/j.memsci.2025.123973.
- S. Yi, X. Ma, I. Pinnau and W. J. Koros, A high-performance hydroxyl-functionalized polymer of intrinsic microporosity for an environmentally attractive membrane-based approach to decontamination of sour natural gas, J. Mater. Chem. A, 2015, 3(45), 22794–22806, 10.1039/c5ta05928c.
- S. Yi, B. Ghanem, Y. Liu, I. Pinnau and W. J. Koros, Ultraselective glassy polymer membranes with unprecedented performance for energy-efficient sour gas separation, Sci. Adv., 2019, 5(5), eaaw5459, DOI:10.1126/sciadv.aaw5459.
- P. A. Dean, K. Mizrahi Rodriguez, S. Guo, N. Roy, T. M. Swager and Z. P. Smith, Elucidating the role of micropore-generating backbone motifs and amine functionality on H2S, CO2, CH4 and N2 sorption, J. Membr. Sci., 2024, 696, 122465, DOI:10.1016/j.memsci.2024.122465.
- K. Mizrahi Rodriguez, P. A. Dean, S. Guo, N. Roy, T. M. Swager and Z. P. Smith, Elucidating the role of micropore-generating backbone motifs and amine functionality on membrane separation performance in complex mixtures, J. Membr. Sci., 2024, 696, 122464, DOI:10.1016/j.memsci.2024.122464.
- D. R. Paul, Effect of immobilizing adsorption on the diffusion time lag, J. Polym. Sci., Part A-2, 1969, 7(10), 1811–1818, DOI:10.1002/pol.1969.160071015.
- G. H. Fredrickson and E. Helfand, Dual-mode transport of penetrants in glassy polymers, Macromolecules, 1985, 18(11), 2201–2207, DOI:10.1021/ma00153a024.
- S. Kanehashi and K. Nagai, Analysis of dual-mode model parameters for gas sorption in glassy polymers, J. Membr. Sci., 2005, 253(1), 117–138, DOI:10.1016/j.memsci.2005.01.003.
- W. J. Koros, R. T. Chern, V. Stannett and H. B. Hopfenberg, A model for permeation of mixed gases and vapors in glassy polymers, J. Polym. Sci., Polym. Phys. Ed., 1981, 19(10), 1513–1530, DOI:10.1002/pol.1981.180191004.
- E. Ricci and M. G. De Angelis, Modelling mixed-gas sorption in glassy polymers for CO2 removal: a sensitivity analysis of the dual mode sorption model, Membranes, 2019, 9(1), 8, DOI:10.3390/membranes9010008.
- A. X. Wu, J. A. Drayton, K. Mizrahi Rodriguez, F. M. Benedetti, Q. Qian, S. Lin and Z. P. Smith, Elucidating the role of fluorine content on gas sorption properties of fluorinated polyimides, Macromolecules, 2021, 54(1), 22–34, DOI:10.1021/acs.macromol.0c01746.
- R. M. Barrer, J. A. Barrie and N. K. Raman, Solution and diffusion in silicone rubber I—A comparison with natural rubber, Polymer, 1962, 3, 595–603, DOI:10.1016/0032-3861(62)90108-8.
- Z. P. Smith, R. R. Tiwari, T. M. Murphy, D. F. Sanders, K. L. Gleason, D. R. Paul and B. D. Freeman, Hydrogen sorption in polymers for membrane applications, Polymer, 2013, 54(12), 3026–3037, DOI:10.1016/j.polymer.2013.04.006.
- W. J. Koros, D. R. Paul and G. S. Huvard, Energetics of gas sorption in glassy polymers, Polymer, 1979, 20(8), 956–960, DOI:10.1016/0032-3861(79)90192-7.
- L. J. Abbott, K. E. Hart and C. M. Colina, Polymatic: a generalized simulated polymerization algorithm for amorphous polymers, Theor. Chem. Acc., 2013, 132(3), 1334, DOI:10.1007/s00214-013-1334-z.
- G. S. Larsen, P. Lin, K. E. Hart and C. M. Colina, Molecular simulations of PIM-1-like polymers of intrinsic microporosity, Macromolecules, 2011, 44(17), 6944–6951, DOI:10.1021/ma200345v.
- L. Abbott; C. Colina Polymatic: a simulated polymerization algorithm, 2013. https://nanohub.org/resources/17278, accessed 2024-11-21.
- W. J. Morgan, D. M. Anstine and C. M. Colina, Temperature effects in flexible adsorption processes for amorphous microporous polymers, J. Phys. Chem. B, 2022, 126(33), 6354–6365, DOI:10.1021/acs.jpcb.2c04543.
- G. Kupgan, A. G. Demidov and C. M. Colina, Plasticization behavior in polymers of intrinsic microporosity (PIM-1): A simulation study from combined Monte Carlo and molecular dynamics, J. Membr. Sci., 2018, 565, 95–103, DOI:10.1016/j.memsci.2018.08.004.
- D. M. Anstine, A. G. Demidov, N. F. Mendez, W. J. Morgan and C. M. Colina, Screening PIM-1 performance as a membrane for binary mixture separation of gaseous organic compounds, J. Membr. Sci., 2020, 599, 117798, DOI:10.1016/j.memsci.2019.117798.
- G. Kupgan, T. P. Liyana-Arachchi and C. M. Colina, NLDFT pore size distribution in amorphous microporous materials, Langmuir, 2017, 33(42), 11138–11145, DOI:10.1021/acs.langmuir.7b01961.
- D. N. Theodorou and U. W. Suter, Detailed molecular structure of a vinyl polymer glass, Macromolecules, 1985, 18(7), 1467–1478, DOI:10.1021/ma00149a018.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- M. G. Martin and J. I. Siepmann, Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes, J. Phys. Chem. B, 1998, 102(14), 2569–2577, DOI:10.1021/jp972543+.
- M. G. Martin and J. I. Siepmann, Novel configurational-bias Monte Carlo method for branched molecules. Transferable potentials for phase equilibria. 2. United-atom description of branched alkanes, J. Phys. Chem. B, 1999, 103(21), 4508–4517, DOI:10.1021/jp984742e.
- J.-S. Lee, C. D. Wick, J. M. Stubbs and J. I. Siepmann, Simulating the vapour–liquid equilibria of large cyclic alkanes, Mol. Phys., 2005, 103(1), 99–104, DOI:10.1080/00268970412331303341.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general Amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174, DOI:10.1002/jcc.20035.
- X. He, V. H. Man, W. Yang, T.-S. Lee and J. Wang, A fast and high-quality charge model for the next generation general AMBER force field, J. Chem. Phys., 2020, 153(11), 114502, DOI:10.1063/5.0019056.
- J. J. Potoff and J. I. Siepmann, Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen, AIChE J., 2001, 47(7), 1676–1682, DOI:10.1002/aic.690470719.
- L. Zhang and J. I. Siepmann, Direct calculation of Henry's law constants from Gibbs ensemble Monte Carlo simulations: nitrogen, oxygen, carbon dioxide and methane in ethanol, Theor. Chem. Acc., 2006, 115(5), 391–397, DOI:10.1007/s00214-005-0073-1.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97(40), 10269–10280, DOI:10.1021/j100142a004.
- E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, R. E. D. Server: a web service for deriving RESP and ESP charges and building force field libraries for new molecules and molecular fragments, Nucleic Acids Res., 2011, 39, W511–W517, DOI:10.1093/nar/gkr288.
- M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; G. A. Petersson; H. Nakatsuji; X. Li; M. Caricato; A. V. Marenich; J. Bloino; B. G. Janesko; R. Gomperts; B. Mennucci; H. P. Hratchian; J. V. Ortiz; A. F. Izmaylov; J. L. Sonnenberg; F. Williams; Ding; F. Lipparini; F. Egidi; J. Goings; B. Peng; A. Petrone; T. Henderson; D. Ranasinghe; V. G. Zakrzewski; J. Gao; N. Rega; G. Zheng; W. Liang; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell; J. A. Montgomery Jr.; J. E. Peralta; F. Ogliaro; M. J. Bearpark; J. J. Heyd; E. N. Brothers; K. N. Kudin; V. N. Staroverov; T. A. Keith; R. Kobayashi; J. Normand; K. Raghavachari; A. P. Rendell; J. C. Burant; S. S. Iyengar; J. Tomasi; M. Cossi; J. M. Millam; M. Klene; C. Adamo; R. Cammi; J. W. Ochterski; R. L. Martin; K. Morokuma; O. Farkas; J. B. Foresman; D. J. Fox Gaussian 16 Rev. C.01, 2016 Search PubMed.
- F.-Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, R. Lelong, N. Grivel, D. Lelong, W. Rosanski, P. Cieplak and R. E. D. The, tools: advances in RESP and ESP charge derivation and force field library building, Phys. Chem. Chem. Phys., 2010, 12(28), 7821–7839, 10.1039/c0cp00111b.
- M. L. Connolly, Analytical molecular surface calculation, J. Appl. Crystallogr., 1983, 16(5), 548–558, DOI:10.1107/s0021889883010985.
- C. M. Davel, T. Bernat, J. R. Wagner and M. R. Shirts, Parameterization of general organic polymers within the open force field framework, J. Chem. Inf. Model., 2024, 64(4), 1290–1305, DOI:10.1021/acs.jcim.3c01691.
- S. Patel and C. L. Brooks III, CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations, J. Comput. Chem., 2004, 25(1), 1–16, DOI:10.1002/jcc.10355.
- A. S. Teja, R. J. Lee, D. Rosenthal and M. Anselme, Correlation of the critical properties of alkanes and alkanols, Fluid Phase Equilib., 1990, 56, 153–169, DOI:10.1016/0378-3812(90)85100-o.
- G. C. Maitland, M. Rigby, B. Smith and W. A. Wakeham, Intermolecular Forces: Their Origin and Determination, International Series of Monographs on Chemistry, Oxford University Press, Oxford, 1987 Search PubMed.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, 1988, DOI:10.1201/9780367806934.
- Homogeneous flows for atomic fluids: Theory, in Nonequilibrium Molecular Dynamics: Theory, Algorithms and Applications, ed. B. D. Todd and P. J. Daivis, Cambridge University Press, Cambridge, 2017, pp. 104–149, DOI:10.1017/9781139017848.006.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A, 1985, 31(3), 1695–1697, DOI:10.1103/physreva.31.1695.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519, DOI:10.1063/1.447334.
- S. Nosé, A molecular dynamics method for simulations in the Canonical ensemble, Mol. Phys., 1984, 52(2), 255–268, DOI:10.1080/00268978400101201.
- M. Tuckerman, B. J. Berne and G. J. Martyna, Reversible multiple time scale molecular dynamics, J. Chem. Phys., 1992, 97(3), 1990–2001, DOI:10.1063/1.463137.
- L. Verlet, Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules, Phys. Rev., 1967, 159(1), 98–103, DOI:10.1103/physrev.159.98.
- Q. Yang and C. Zhong, Molecular simulation of adsorption and diffusion of hydrogen in metal−organic frameworks, J. Phys. Chem. B, 2005, 109(24), 11862–11864, DOI:10.1021/jp051903n.
- M. Barraco, S. Neyertz, N. E. Benes and D. Brown, Comparison of eight classical Lennard-Jones-based H2 molecular models in the gas phase at temperatures and pressures relevant to hydrogen on-board storage tanks, J. Phys. Chem. A, 2023, 127(30), 6335–6346, DOI:10.1021/acs.jpca.3c03212.
- M. S. Shah, M. Tsapatsis and J. I. Siepmann, Development of the transferable potentials for phase equilibria model for hydrogen sulfide, J. Phys. Chem. B, 2015, 119(23), 7041–7052, DOI:10.1021/acs.jpcb.5b02536.
- J. K. Shah, E. Marin-Rimoldi, R. G. Mullen, B. P. Keene, S. Khan, A. S. Paluch, N. Rai, L. L. Romanielo, T. W. Rosch, B. Yoo and E. J. Maginn, Cassandra: An open source Monte Carlo package for molecular simulation, J. Comput. Chem., 2017, 38(19), 1727–1739, DOI:10.1002/jcc.24807.
- M. E. Fortunato, A. G. Demidov, S. Lin, P. Lin, K. Leon, B. L. A. Perera, B. C. Tapia and C. M. Colina, SmithLabMIT/pysimm: v1.1.1, 2025, DOI:10.5281/zenodo.17247184.
- M. E. Fortunato; A. G. Demidov; S. Lin; P. Lin; L. Kwan; B. L. A. Perera; C. M. Colina polysimtools/pysimm, 2024. https://github.com/polysimtools/pysimm, accessed 2024-11-21.
- M. E. Fortunato and C. M. Colina, pysimm: A python package for simulation of molecular systems, SoftwareX, 2017, 6, 7–12, DOI:10.1016/j.softx.2016.12.002.
- A. G. Demidov, M. E. Fortunato and C. M. Colina, Update 0.2 to “pysimm: A Python package for simulation of molecular systems.”, SoftwareX, 2018, 7, 70–73, DOI:10.1016/j.softx.2018.02.006.
- A. G. Demidov, B. L. A. Perera, M. E. Fortunato, S. Lin and C. M. Colina, Update 1.1 to “pysimm: A Python package for simulation of molecular systems.”, SoftwareX, 2021, 15, 100749, DOI:10.1016/j.softx.2021.100749.
- P. R. Bevington and D. K. Robinson, Data Reduction and Error Analysis for the Physical Sciences, McGraw-Hill, 2003 Search PubMed.
- S. Neyertz and D. Brown, Single- and mixed-gas sorption in large-scale molecular models of glassy bulk polymers. Competitive sorption of a binary CH4/N2 and a ternary CH4/N2/CO2 mixture in a polyimide membrane, J. Membr. Sci., 2020, 614, 118478, DOI:10.1016/j.memsci.2020.118478.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9(7), 671–675, DOI:10.1038/nmeth.2089.
- P. C. Hansen and D. P. O'Leary, The use of the L-curve in the regularization of discrete ill-posed problems, SIAM J. Sci. Comput., 1993, 14(6), 1487–1503, DOI:10.1137/0914086.
- K. Mizrahi Rodriguez, F. M. Benedetti, N. Roy, A. X. Wu and Z. P. Smith, Sorption-enhanced mixed-gas transport in amine functionalized polymers of intrinsic microporosity (PIMs), J. Mater. Chem. A, 2021, 9(41), 23631–23642, 10.1039/d1ta06530k.
- L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Materials informatics with PoreBlazer v4.0 and the CSD MOF database, Chem. Mater., 2020, 32(23), 9849–9867, DOI:10.1021/acs.chemmater.0c03575.
- J.-J. Shieh and T. S. Chung, Gas permeability, diffusivity, and solubility of poly(4-vinylpyridine) film, J. Polym. Sci., Part B: Polym. Phys., 1999, 37(20), 2851–2861, DOI:10.1002/(sici)1099-0488(19991015)37:20<2851::aid-polb5>3.0.co;2-u.
- T. Lodge and P. C. Hiemenz, Polymer Chemistry, CRC Press, Taylor & Francis Group, 3rd edn, 2020 Search PubMed.
- Z. Tang and S. Okazaki, All-atomistic molecular dynamics study of the glass transition of amorphous polymers, Polymer, 2022, 254, 125044, DOI:10.1016/j.polymer.2022.125044.
- M. Klajmon, V. Aulich, J. Ludík and C. Červinka, Glass transition and structure of organic polymers from all-atom molecular simulations, Ind. Eng. Chem. Res., 2023, 62(49), 21437–21448, DOI:10.1021/acs.iecr.3c03038.
- P. Sharma, S. Roy and H. A. Karimi-Varzaneh, Validation of force fields of rubber through glass-transition temperature calculation by microsecond atomic-scale molecular dynamics simulation, J. Phys. Chem. B, 2016, 120(7), 1367–1379, DOI:10.1021/acs.jpcb.5b10789.
- J. Han, R. H. Gee and R. H. Boyd, Glass transition temperatures of polymers from molecular dynamics simulations, Macromolecules, 1994, 27(26), 7781–7784, DOI:10.1021/ma00104a036.
- A. V. Lyulin, N. K. Balabaev and M. A. J. Michels, Molecular-weight and cooling-rate dependence of simulated Tg for amorphous polystyrene, Macromolecules, 2003, 36(22), 8574–8575, DOI:10.1021/ma034406i.
- A. Karuth, A. Alesadi, W. Xia and B. Rasulev, Predicting glass transition of amorphous polymers by application of cheminformatics and molecular dynamics simulations, Polymer, 2021, 218, 123495, DOI:10.1016/j.polymer.2021.123495.
- W. Paul and G. D. Smith, Structure and dynamics of amorphous polymers: computer simulations compared to experiment and theory, Rep. Prog. Phys., 2004, 67(7), 1117, DOI:10.1088/0034-4885/67/7/r03.
- L. Dubrovinsky, Thermal expansion and equation of state, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer, S. Mahajan and P. Veyssière, Elsevier, Oxford, 2002, pp. 1–4, DOI:10.1016/b0-08-043152-6/01817-9.
- E. A. Grulke, D. R. Bloch, A. Akihiro, J. Brandrup and H. I. Edmund, Physical constants of some important polymers, in Polymer Handbook, John Wiley & Sons, 1999 Search PubMed.
- R. F. Clash Jr and L. M. Rynkiewicz, Thermal expansion properties of plastic materials, Ind. Eng. Chem., 1944, 36(3), 279–282, DOI:10.1021/ie50411a021.
- M. Yamato, A. Imai and H. Kawakami, Thermal properties of polymer with intrinsic microporosity membranes, Polymer, 2022, 259, 125339, DOI:10.1016/j.polymer.2022.125339.
- N. A. Seaton, J. P. R. B. Walton and N. Quirke, A new analysis method for the determination of the pore size distribution of porous carbons from nitrogen adsorption measurements, Carbon, 1989, 27(6), 853–861, DOI:10.1016/0008-6223(89)90035-3.
- C. Lastoskie, K. E. Gubbins and N. Quirke, Pore size distribution analysis of microporous carbons: a density functional theory approach, J. Phys. Chem., 1993, 97(18), 4786–4796, DOI:10.1021/j100120a035.
- H.-G. Peng, R. S. Vallery, M. Liu, M. Skalsey and D. W. Gidley, Depth-profiled positronium annihilation lifetime spectroscopy on porous films, Colloids Surf., A, 2007, 300(1), 154–161, DOI:10.1016/j.colsurfa.2006.10.072.
- R. Hou, S. J. D. Smith, K. Konstas, M. Doherty, C. D, C. Easton, J. Park, H. Yoon, H. Wang, D. Freeman and B. R. Hill, M. Synergistically improved PIM-1 membrane gas separation performance by PAF-1 incorporation and UV irradiation, J. Mater. Chem. A, 2022, 10(18), 10107–10119, 10.1039/d2ta00138a.
- S. Le Roux and V. Petkov, ISAACS – interactive structure analysis of amorphous and crystalline systems, J. Appl. Crystallogr., 2010, 43(1), 181–185, DOI:10.1107/s0021889809051929.
- L. Makowski, Characterization of proteins with wide-angle X-ray solution scattering (WAXS), J. Struct. Funct. Genomics, 2010, 11(1), 9–19, DOI:10.1007/s10969-009-9075-x.
- J. H. Dymond, R. C. Wilhoit, K. N. Marsh and K. C. Wong, Virial coefficients of pure gases, Landolt-Börnstein - Group IV Physical Chemistry, ed. M. Frenkel, K. N. Marsh, Springer-Verlag, Berlin/Heidelberg, 2002; Vol. 21A, DOI:10.1007/b71692.
- L. Canti Theoretical modeling of gas adsorption in microporous aromatic polymers, University of Eastern Piedmont, Vercelli, Italy, 2016. doi: DOI:10.20373/uniupo/openthesis/81935.
- Y. Yoshimoto, Y. Tomita, K. Sato, S. Higashi, M. Yamato, S. Takagi, H. Kawakami and I. Kinefuchi, Gas adsorption and diffusion behaviors in interfacial systems composed of a polymer of intrinsic microporosity and amorphous silica: a molecular simulation study, Langmuir, 2022, 38(24), 7567–7579, DOI:10.1021/acs.langmuir.2c00661.
- P. J. Linstrom and W. G. Mallard, The NIST Chemistry WebBook: A chemical data resource on the internet, J. Chem. Eng. Data, 2001, 46(5), 1059–1063, DOI:10.1021/je000236i.
- D.-Y. Peng and D. B. Robinson, A new two-constant equation of state, Ind. Eng. Chem. Fundam., 1976, 15(1), 59–64, DOI:10.1021/i160057a011.
- M. Balçık, S. B. Tantekin-Ersolmaz, I. Pinnau and M. G. Ahunbay, CO2/CH4 mixed-gas separation in PIM-1 at high pressures: Bridging atomistic simulations with process modeling, J. Membr. Sci., 2021, 640, 119838, DOI:10.1016/j.memsci.2021.119838.
- T. H. Lee and Z. P. Smith, Better standards are needed for membrane materials, Nat. Mater., 2024, 23(1), 11–12, DOI:10.1038/s41563-023-01763-2.
- S. Neyertz, N. E. Benes and D. Brown, Molecular simulations of hybrid cross-linked membranes for H2S gas separation at very high temperatures and pressure: Binary 90%/10% N2/H2S and CH4/H2S, ternary 90%/9%/1% N2/CO2/H2S and CH4/CO2/H2S mixtures, J. Membr. Sci., 2023, 687, 122092, DOI:10.1016/j.memsci.2023.122092.
- W. J. Koros and D. R. Paul, CO2 sorption in poly(ethylene terephthalate) above and below the glass transition, J. Polym. Sci., Polym. Phys. Ed., 1978, 16(11), 1947–1963, DOI:10.1002/pol.1978.180161105.
- C. Tofallis, A better measure of relative prediction accuracy for model selection and model estimation, J. Oper. Res. Soc. Am., 2015, 66(8), 1352–1362, DOI:10.1057/jors.2014.103.
- H. Yoshimizu, S. Ohta, T. Asano, T. Suzuki and Y. Tsujita, Temperature dependence of the mean size of polyphenyleneoxide microvoids, as studied by Xe sorption and 129Xe NMR chemical shift analyses, Polym. J., 2012, 44(8), 821–826, DOI:10.1038/pj.2012.123.
- P. Li, T. S. Chung and D. R. Paul, Temperature dependence of gas sorption and permeation in PIM-1, J. Membr. Sci., 2014, 450, 380–388, DOI:10.1016/j.memsci.2013.09.030.
- R. D. Nelson, D. R. Lide and A. A. Maryott, Selected Values of Electric Dipole Moments for Molecules in the Gas phase, National Standards Reference Data Series; NSRDS-NBS 10, National Institute of Standards and Technology, Gaithersburg, MD, 1967. DOI: DOI:10.6028/NBS.NSRDS.10.
- B. W. C. Chen and C. P. O'Brien, Highly selective propylene/propane separation using amine-modified PIM-1 (PIM-NH2), J. Membr. Sci., 2025, 731, 124229, DOI:10.1016/j.memsci.2025.124229.
- W. C. Kuah, S. Effendy and S. Farooq, Industrial scale propylene/propane separation using pressure vacuum swing adsorption, Ind. Eng. Chem. Res., 2018, 57(18), 6451–6463, DOI:10.1021/acs.iecr.8b00289.
- S. Sridhar and A. A. Khan, Simulation studies for the separation of propylene and propane by ethylcellulose membrane, J. Membr. Sci., 1999, 159(1), 209–219, DOI:10.1016/s0376-7388(99)00061-7.
| This journal is © The Royal Society of Chemistry 2026 |