Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predictive thermal safety of lithium-ion batteries through a unified kinetic-thermal framework
Jiale Huang a,
Yiyang Xia
a,
Yiyang Xia a,
Shijia Xua,
Ling Lia,
Hongbo Jia,
Xiaoping Chen*a and
Jun Xu
a,
Shijia Xua,
Ling Lia,
Hongbo Jia,
Xiaoping Chen*a and
Jun Xu *bc
*bc
aZhejiang Provincial International Joint Laboratory of New Energy Vehicle Technology, College of Mechanical and Automotive Engineering, Ningbo University of Technology, Ningbo, China. E-mail: cxp@nbut.edu.cn
bDepartment of Mechanical Engineering, University of Delaware, Newark, DE 19716, USA. E-mail: junxu@udel.edu
cEnergy Mechanics and Sustainability Laboratory (EMSLab), University of Delaware, Newark, DE 19716, USA
First published on 11th December 2025
Abstract
Thermal runaway remains a critical barrier to the safe deployment of high-energy lithium-ion batteries. Here, we establish a unified quantitative framework that integrates intrinsic reaction kinetics with thermal transport to predict and design cell-level thermal safety. Accelerating rate calorimetry measurements are employed to resolve temperature-dependent self-heating behaviors across state of charge, providing direct inputs for a physics-based thermal model that captures both internal conduction and boundary convection. Systematic variation of state of charge, surface-to-volume ratio, and convective intensity reveals a distinct critical temperature separating stable and runaway regimes, enabling construction of a comprehensive thermal safety boundary. We show that the surface-to-volume ratio, rather than aspect ratio, serves as the fundamental geometric parameter governing temperature uniformity and heat dissipation. A dimensionless thermal safety criterion is further derived, explicitly linking self-heating to dissipation and allowing direct estimation of safe operating limits without reliance on full CFD simulations. This framework transforms thermal safety evaluation from empirical observation to a predictive, physics-informed design methodology, bridging mechanistic understanding and engineering practice to guide safe operation and scalable thermal management of lithium-ion batteries across chemistries, geometries, and cooling configurations.
1 Introduction
Lithium-ion batteries (LIBs) underpin the rapid expansion of electric vehicles and stationary energy storage systems, placing them at the heart of the global energy transition. However, their susceptibility to safety issues, particularly thermal runaway (TR), a self-accelerating failure process that can culminate in fire or explosion, remains a critical barrier to large-scale deployment.1,2Thermal runaway arises from a cascade of highly exothermic reactions that destabilize the electrochemical system once internal heat generation surpasses heat dissipation.3 Significant progress has been made in characterizing these reactions at the materials level (e.g., solid–electrolyte interphase decomposition, electrolyte oxidation, cathode oxygen release)4–10 and the component level (e.g., electrode–electrolyte interfaces, current collectors, separators).11–16 Advanced diagnostic tools such as accelerating rate calorimetry (ARC),17–20 differential scanning calorimetry (DSC),21,22 and in situ imaging and gas analysis23–25 have revealed the temporal sequence, onset temperatures, and energetics of these reactions. Complementary propagation studies have further elucidated how localized instabilities evolve into full-cell runaway by coupling reaction kinetics, heat generation, and thermal transport.26–29 Collectively, these investigations have established a detailed mechanistic understanding of TR initiation and evolution.
At the cell scale, however, thermal runaway is governed not only by chemical reactivity but by the dynamic competition between internal heat generation and external heat dissipation. This balance is strongly influenced by state of charge (SOC),30 intrinsic thermal conductivity and anisotropy,31 and boundary cooling conditions.32 When self-heating exceeds heat dissipation, nonlinear positive feedback leads to rapid temperature escalation. Although prior studies have proposed critical temperatures or heat generation thresholds,33–36 such criteria are typically geometry- or condition-specific. For instance, while geometric metrics like the aspect ratio are often used to characterize cell shape, they primarily describe the internal heat conduction distance. They fail to capture the fundamental competition between volumetric heat generation and surficial heat dissipation. Recently, data-driven approaches, particularly machine learning, have emerged as promising tools for predicting thermal runaway risks by learning complex nonlinear patterns from large datasets.37 In this light, combing data-driven insights with physics-based transport laws offers a robust pathway for safety prediction. Consequently, a unified, quantitative, and physically grounded thermal safety criterion that incorporates capacity, geometry, and environmental factors remains elusive.
To address this gap, we develop a comprehensive framework that explicitly couples intrinsic heat generation with external heat dissipation to construct a mechanistic thermal safety boundary for cylindrical LIBs. First, intrinsic self-heating behavior across SOCs is experimentally quantified using ARC under adiabatic conditions, providing temperature-dependent heat generation profiles. These data are integrated into a three-dimensional thermal model that resolves internal conduction and boundary convection under varying cooling intensities. By systematically varying SOC, surface-to-volume ratio, and convective heat transfer coefficient, we identify the critical temperature separating stable and runaway regimes. To generalize these discrete results, a random forest model is trained to construct a continuous, predictive thermal safety boundary. Finally, inspired by Semenov's thermal explosion theory, we derive a dimensionless thermal safety criterion (TSC) that quantitatively balances self-heating and dissipation, enabling rapid estimation of safe operating limits without full computational fluid dynamics (CFD) simulations.
Unlike case-specific thresholds or purely empirical approaches, this unified kinetic–thermal framework is physics-informed, scalable, and directly applicable to design. By integrating experimental calorimetry, numerical modeling, machine learning, and theoretical analysis, this work transforms thermal safety evaluation from empirical observation into a predictive, design-oriented methodology for assessing and optimizing the thermal stability of lithium-ion batteries across chemistries, geometries, and cooling strategies.
2 Thermodynamics of thermal runaway
2.1. Thermal runaway characteristics
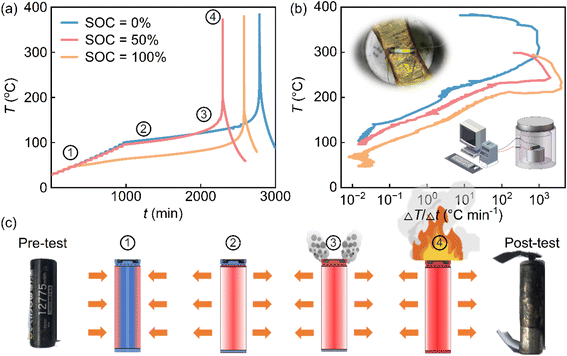
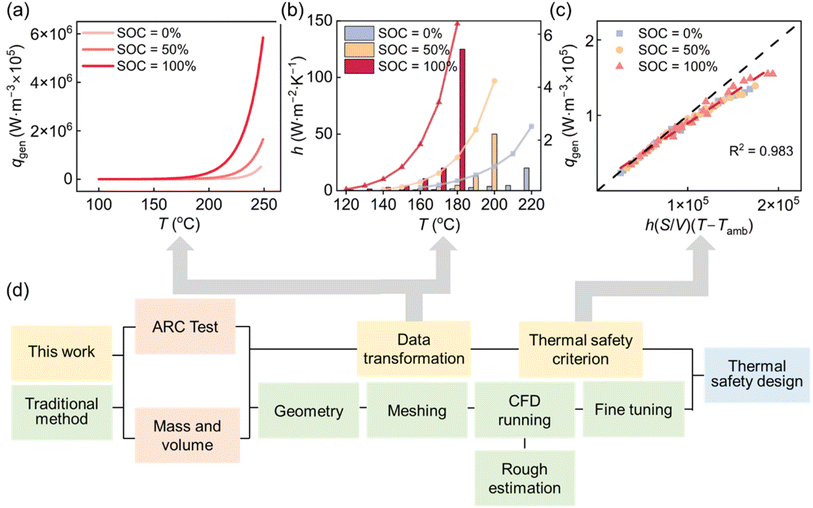
The TR behavior of a commercial 18650 NCM cylindrical cell was evaluated using ARC under adiabatic self-heating conditions representative of worst-case failure scenarios. Prior to testing, the cell's physical properties and cycling consistency were verified to ensure data reliability (Fig. S1).Despite differences in stored energy, all cells follow four characteristic stages: (1) heat-wait-seek, (2) self-heating, (3) venting, and (4) runaway. However, the onset temperature of self-heating is strongly SOC-dependent (Fig. 1(a)). At 100% SOC, self-heating begins near 48 °C, whereas at 0% and 50% SOC it is delayed until 100 °C, reflecting the increased reactivity of high-energy cathode, electrolyte, and anode interfaces at elevated SOCs. In the meantime, the transition temperature to runaway decreases with increasing SOC, reflecting that enhanced reactivity has a consistent trend that aligns with the four stages. The peak temperature during runaway exceeds 370 °C. It is noted that the recorded maximum temperatures across different SOCs are similar. However, this is attributed to the mechanical detachment of the thermocouples caused by violent gas release and combustion, which prevents the capture of the true maximum temperature. Nevertheless, the kinetic parameters derived from the earlier self-heating phase remain continuous and reliable, providing sufficient input for the thermal safety model.
The corresponding temperature rise rates (Fig. 1(b)) reveal the dynamic nature of the runaway process. Below 100 °C, the temperature evolution is dominated by ARC's controlled heating protocol. Once self-heating initiates, the rate increases exponentially with temperature, reflecting the kinetic acceleration of exothermic reactions. At comparable temperatures, higher SOCs exhibit markedly steeper rise rates, confirming that cells sorting more energy not only generate more heat but also accelerate feedback-driven instability.
Prior to self-heating, heat is externally supplied and partially dissipated through the cell surface (Fig. 1(c)). Once self-heating begins, external heating is disabled and the system transitions to a quasi-adiabatic state, where temperature evolution is governed almost entirely by internal reaction kinetics. Pre- and post-test photographs further confirm severe deformation and rupture, consistent with rapid internal pressure buildup during the runaway event (Fig. 1(c)). The measured temperature rise rate was then converted into the heat generation rate using
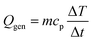 | (1) |
2.2. Determination of critical temperature
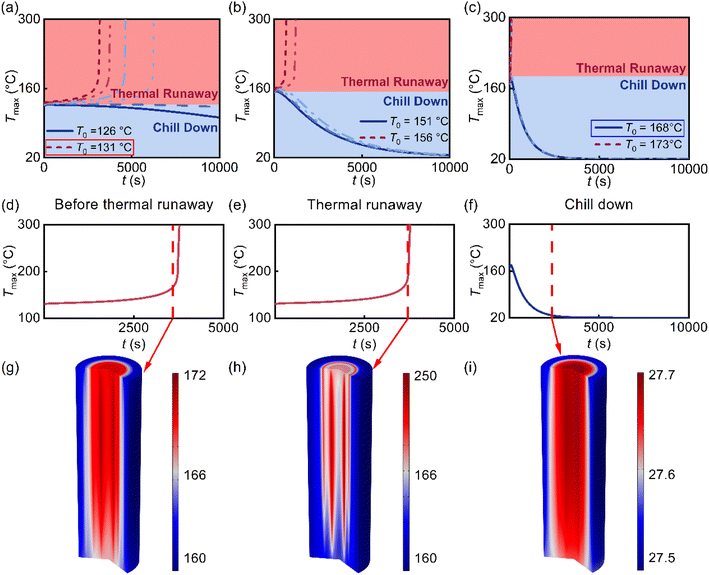
A numerical simulation framework was developed to resolve the coupled thermal processes governing the transition between stabilization and runaway. The model captures internal conduction and surface convection under externally imposed initial temperature conditions. Throughout the simulations, the ambient temperature Tamb was fixed at 25 °C, while the initial cell temperature T0 was systematically varied to determine the stability threshold. It is also worth noting that the simulations are initialized with a uniform temperature field, whereas real-world abuse scenarios often involve thermal gradients. This uniform initialization serves as a conservative design assumption. The thermal properties of the cell, anisotropic thermal conductivity (Fig. S2 and S3) and specific heat capacity (Fig. S4) have been carefully measured. The grid and time-step independence have been verified (Fig. S5). To determine the threshold for thermal failure, the initial cell temperature was systematically varied in 1 °C increments. For each numerical simulation, a virtual probe recorded the peak temperature in the domain, enabling classification of the final state as either chill down or runaway.For a 100% SOC 18650 cell subjected to convective coefficients of 1, 5, and 20 W m−2 K−1, representative initial temperature windows of 126–131 °C, 151–156 °C, and 168–173 °C were examined, respectively (Fig. 2(a)–(c)). Two distinct regimes emerged. In the runway regime, internal thermal feedback dominated, and the temperature diverged rapidly. In the chill-down regime, the cell cooled back to equilibrium as heat removal dominated over self-heating. Additionally, Fig. 2(d)–(f) present the temporal evolution of the maximum temperature for three representative cases: prior to runaway initiation, at the onset of thermal runaway, and during the stabilization phase of chill-down. The critical temperature Tc was thus defined as the highest initial condition that still results in stabilization, providing a quantitative boundary between safe and unsafe thermal trajectories.
To clarify the underlying physics, three representative states were extracted from the simulations (Fig. 2(g)–(i)). In the pre-runaway stage (h = 1 W m−2 K−1, T0 = 130 °C), internal temperature ranged only from 160 °C to 172 °C, indicating efficient heat redistribution through conduction and moderate surface losses. Once the runaway was triggered, the peak temperature surged to 250 °C within seconds, and a pronounced spatial gradient emerged, signifying strong positive feedback and loss of thermal equilibrium. In contrast, under high convection (h = 20 W m−2 K−1, T0 = 168 °C), the system remained thermally stable and nearly isothermal, with <0.2 °C variation across the domain.
These results clearly demonstrate that the transition between stabilization and runaway is governed by the interplay between intrinsic reaction kinetics and external heat removal capacity. The identified Tc thus serves as a mechanistic indicator of the boundary separating self-limiting and self-accelerating thermal responses in lithium-ion cells.
3 Interplay of heat dissipation and geometry in thermal stability
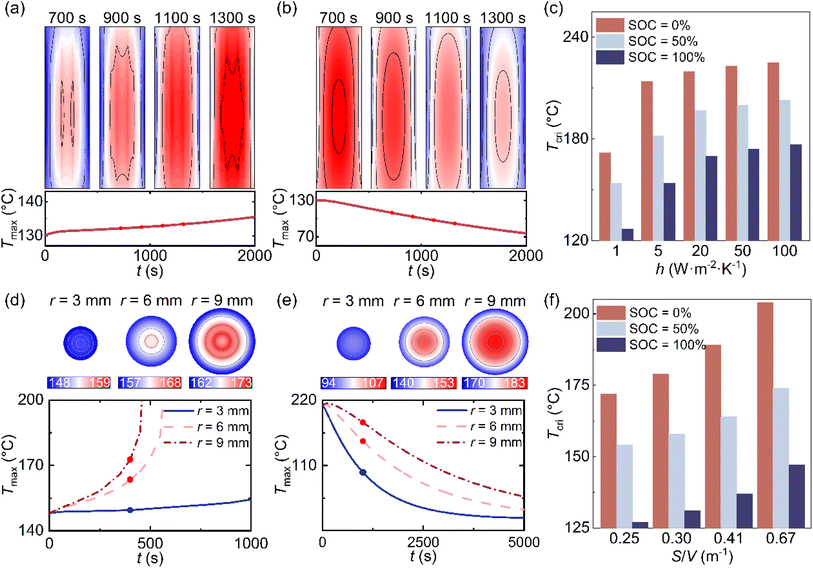
Beyond SOC, thermal stability in lithium-ion cells is strongly governed by two system-level factors: the external thermal environment and the cell geometry. The former dictates the rate of heat removal through surface convection, while the latter influences both internal temperature uniformity and the efficiency of boundary-mediated dissipation.During external heating, the front develops in an irregular, nonuniform pattern due to the nonlinear temperature dependences of reaction kinetics (Fig. 3(a) and (b)). In contrast, during cooling, the front becomes elliptical, shaped by the near-linear decay of temperature and the intrinsic anisotropy of thermal conductivity within the jelly-roll structure. This directional dependence underscores that thermal runaway onset is not purely kinetically controlled but also governed by spatial heat transport. Increasing the external heat transfer coefficient shifts the system toward greater stability, raising the threshold for runway (Fig. 3(c)). However, beyond approximately 20 W m−2 K−1, further increases yield diminishing returns, marking a practical upper limit for forced-air cooling in realistic designs. Beyond this threshold, geometric or material-level optimization is required to achieve additional safety margins.
While the aspect ratio has been widely used to describe geometric effects in prior studies, impacting heat spreading,38 propagation velocity,39 and convective performance,40–43 it treats geometry primarily as a shape descriptor and does not explicitly couple internal transport with external removal. This raises the question of whether the aspect ratio can serve as a universal indicator when heat release and thermal extraction act simultaneously. The surface-to-volume ratio (S/V) provides a more physically grounded metric, as it directly represents the balance between heat accumulation and the surface-mediated dissipation. Its relevance has been demonstrated in systems ranging from biological heat regulation to ionic transport in electrochemical cells.44–46 It is acknowledged that due to the anisotropic thermal conductivity of LIBs, the aspect ratio influences the internal heat conduction path and temperature uniformity. However, for the determination of the critical thermal safety boundary, the global energy balance is paramount. Since intrinsic heat generation is volumetric while dissipation is surficial, the competition between these two fluxes is mathematically governed by the surface-to-volume ratio (S/V). Consequently, laboratory-scale runaway studies have linked S/V to the rate of temperature escalation,47 confirming its role as the dominant geometric criterion for macro-scale safety evaluation. Theoretical modeling (Fig. S6) and parametric investigations (Fig. S7) further confirm that S/V intrinsically governs the transient thermal response of reactive solids.48
To isolate the impact of geometric configuration on thermal stability, the parametric study in Fig. 3(d) and (e) was conducted under a constant total volume constraint. Consequently, the total heat generation power remained identical across all cases, ensuring that the variations in temperature distribution were driven solely by the differences in internal thermal conduction resistance and surface dissipation area, rather than variations in total thermal energy. Across all SOCs, the critical temperature increases monotonically with S/V, demonstrating that the enhanced surface accessibility improves both energy dissipation and temperature homogenization. Collectively, these results establish S/V as a unified geometric parameter that captures the coupled effects of heat redistribution and boundary interaction, enabling more accurate prediction and design of thermal safety thresholds than aspect ratio alone. It is worth noting, however, that the metric assumes the internal heat transport is sufficient to utilize the available surface area. In cell geometries with extreme aspect ratios, such as very elongated or extremely flat configurations, the significant thermal anisotropy could lead to directional heat transfer bottlenecks. In such limit cases, the preferred direction of heat flow might decouple the effective cooling area from the total surface area, potentially complicating the single dependence on S/V. Nevertheless, for standard cylindrical form factors, S/V remains the dominant predictor of the global thermal safety boundary.
4 Predictive mapping of thermal stability regimes
4.1. Construction of the thermal safety boundary
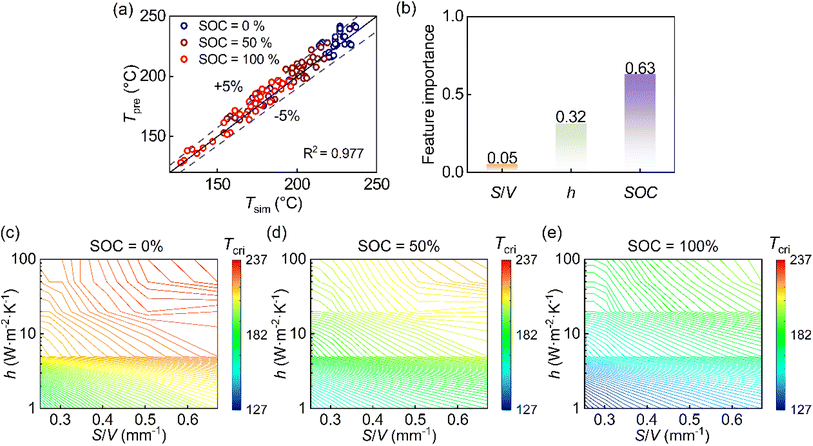
Using the validated simulation dataset spanning SOC, convective intensity, and surface-to-volume ratio, we constructed a thermal safety boundary that defines the maximum initial temperature a cell can withstand without entering runaway. To generalize discrete simulation outputs into a continuous and predictive design space, a machine-learning model based on random forest regression was trained and validated (Fig. S8 and S9).The trained machine-learning model exhibits strong agreement (R2 = 0.977), with >80% of cases within ±5% error and a maximum deviation of 7.54%, demonstrating its robustness in capturing nonlinear interactions among parameters (Fig. 4(a)). The feature importance analysis indicates that SOC is the dominant factor (weight = 0.63) (Fig. 4(b)), reflecting its control over reaction enthalpy and kinetic intensity. The convective parameter (weight = 0.32) ranks second, confirming the substantial impact of thermal management in delaying runaway onset. Although S/V contributes a smaller global weight value (0.05) due to the dominance of convective cooling at high h values, it remains essential in the weak convection regime typical of passive cooling or failure scenarios. Quantitative analysis of the simulation results (Fig. 3(f)) reveals that at h = 1 W m−2 K−1, increasing S/V from 0.25 to 0.67 m−1 raises the critical temperature by more than 20 °C at 50% SOC. This indicates that while geometry is secondary under strong active cooling, it provides a significant safety margin improvement when external heat dissipation is limited.
In the resulting thermal safety boundary as a contour map in the multidimensional parameter space, each contour denotes a critical temperature corresponding to a specific combination of SOC, S/V, and convection level (Fig. 4(c)–(e)). This boundary provides a direct, design-oriented tool: given operating conditions and cell geometry, one can determine the maximum allowable temperature without solving the full thermal model. Conversely, it can be used inversely to identify the minimum cooling requirement or geometric constraint necessary to maintain stability. By integrating the coupled influences of material state, geometry, and environment into a single predictive framework, the thermal safety boundary bridges mechanistic insight with engineering practicality, enabling quantitative design of cell-level safety margins.
4.2. Dimensionless thermal safety criterion
While the thermal safety boundary defines the safe operational envelope implicitly, practical design requires an explicit, physically interpretable stability index. To this end, we derive a dimensionless thermal safety criterion (TSC) grounded in the fundamental energy balance of a reactive system. According to Semenov's theory, thermal stability is achieved when the rate of reaction-driven heat release equals the rate of thermal loss to the surroundings.49 At the critical temperature Tcri, this steady-state balance can be expressed as,| Qgen(Tcri, SOC) = Qdiss(Tcri) | (2) |
| Qgen(T, SOC) = Vqgen(T, SOC) | (3) |
| Qdiss = hS(T − Tamb) | (4) |
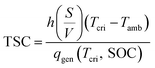 | (5) |
To incorporate realistic effects, we refine the criterion using the previously constructed thermal safety boundary. The ARC-derived qgen (Fig. 5(a)) shows a clear dependency on SOC and increases exponentially above 200 °C. As the heat generation rate rises, greater convective cooling is required for stabilization, highlighting the proportional relationship between dissipation and heat generation (Fig. 5(b)). This aligns with the proportionality implied by eqn (5), suggesting that qgen and h(S/V)(T − Tamb) can be directly regressed. Further, the linear regression (Fig. 5(c)) (R2 = 0.983) confirms the validity of the theoretical framework with minor deviations attributed to replacing surface temperature with the domain maximum in the calculation of T − Tamb. This regression allows for the derivation of the thermal safety criterion, so that we obtain
| TSC = 1.252 | (6) |
This criterion enables a direct pathway to construct thermal safety boundaries without repeated numerical simulations (Fig. 5(d)). Traditionally, determining safe operating limits required extensive meshing, CFD execution, and iterative tuning. In contrast, once qgen(T) is derived from ARC data, the TSC allows immediate calculation of the required product h(S/V) for a target allowable temperature. Engineers can therefore invert the criterion to determine the minimum cooling requirement or optimal geometry needed to prevent runaway.
By distilling a complex thermo-kinetic process into a concise, physics-informed stability index, the dimensionless thermal safety criterion provides a unified tool for cell design, cooling strategy optimization, and rapid safety evaluation across chemistries, geometries, and operational environments.
5 Conclusions
This study establishes a unified and quantitative framework for predicting and designing thermal safety in cylindrical lithium-ion cells by integrating experimentally derived self-heating behavior with numerical simulation and data-driven modeling. Using ARC to capture intrinsic reaction kinetics, we resolved the coupled interaction between internal thermal feedback and external heat removal across a wide design space of state of charge, convective environment, and geometric configuration. From these results, we constructed a thermal safety boundary, identified surface-to-volume as a physically meaningful geometric descriptor, and derived a dimensionless thermal safety criterion that directly links fundamental thermal processes to practical design constraints. Collectively, these advances provide a mechanistic, scalable, and design-oriented pathway for preventing thermal runaway in high-energy lithium-ion cells.5.1. Construction of a thermal safety boundary
Over 300 simulations were performed to identify the critical temperature that separates thermal runaway from stabilization across SOC (0–100%), convection (1–50 W m−2 K−1), and geometry. A random forest model accurately predicted these outcomes (R2 = 0.977, max deviation 7.54%, >80% within 5%), capturing nonlinear interactions between parameters. Feature importance analysis showed SOC as the dominant factor (0.63), followed by convective intensity (0.32) and geometry (0.05). The boundary revealed that increasing cooling capacity shifts cells toward higher stability, but gains plateau beyond 20 W m−2 K−1, establishing a practical benchmark for forced-air thermal management. The resulting map provides a direct tool for determining the maximum allowable temperature under any combination of operating and design parameters.5.2. Surface-to-volume ratio as a unifying geometric metric
We demonstrate that S/V provides a more fundamental and mechanistically grounded geometric parameter than aspect ratio because it simultaneously governs internal temperature uniformity and boundary-mediated heat removal. Increasing S/V from 0.25 to 0.67 m−1 improved thermal homogeneity and raised the critical temperature by more than 20 °C at 50% SOC and h = 1 W m−2 K−1. S/V also modulates the sensitivity of the system to convection. Under weak cooling (h ≤ 5 W m−2 K−1), geometry exerts a strong influence on stability, whereas under strong cooling (h ≥ 20 W m−2 K−1), geometric effects saturate. Thus, S/V serves as a unified metric that captures the coupled influence of internal transport and external dissipation within the thermal safety boundary and provides a design-relevant handle for engineering thermal robustness.5.3. Thermal safety criterion for rapid and physics-informed design
Inspired by Semenov's theory, we derived a dimensionless thermal safety criterion (TSC) that identifies the condition at which thermal feedback is exactly balanced by dissipation. Regression against critical-state simulation data confirmed the linear relationship between volumetric self-heating and h(S/V)(T − Tamb), yielding TSC = 1.252 with R2 = 0.983. Unlike traditional workflows that rely on iterative CFD simulation, the TSC enables direct calculation of the maximum safe operating temperature, or, inversely, the minimum required cooling or geometric configurations from ARC-derived thermal reactivity. This transforms thermal safety evaluation from trial-and-error modeling into an explicit, physics-informed formulation, offering a scalable and practical tool for battery design, parameter optimization, and safety certification.6 Methodology
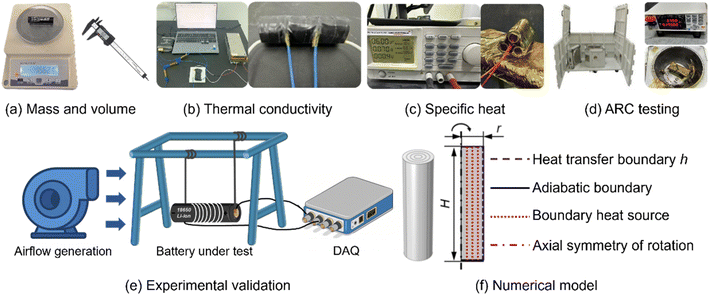
6.1. Cell specifications and preliminary characterization
A commercial 18650-type NCM cell (Delipow, 3500 mA h nominal capacity, 3.7 V nominal voltage, 4.2 V cutoff) was selected for all experiments. To ensure data reliability, a consistency test was performed on ten units using a battery cycler, verifying comparable voltage–capacity behavior over nine charge–discharge cycles (Fig. S1). Fundamental physical properties, including mass, dimensions, and volume, were measured with a high-precision analytical balance (Sartorius BSA224S, 0.1 mg resolution) and a vernier caliper (Fig. 6(a)). The average mass was 4.56 × 10−2 kg, and the density was 2.76 × 103 kg m−3. These measurements enabled calculation of the surface-to-volume (S/V) ratio, a key parameter in the subsequent thermal analysis.6.2. Measurement of thermal transport properties
In cylindrical lithium-ion cells, the jelly-roll structure leads to pronounced anisotropy in thermal transport: the electrode–separator stack acts as a parallel configuration in the radial direction and a series configuration in the axial direction. Consequently, radial thermal conductivity (kr) is typically orders of magnitude lower than axial conductivity (kz).Anisotropic thermal conductivities were measured using a custom-built apparatus equipped with embedded thermocouples and an Agilent 34970A data acquisition system (Fig. 6(b)). Specific heat capacity (cp) was measured using a calibrated heat capacity analyzer (Thermal Hazard Technology) (Fig. 6(c)). Both measurements were obtained within a single experimental sequence (Fig. S2). Heat transfer in the radial direction was modeled as one-dimensional conduction across the cylindrical wall, yielding: kr = 0.178 ± 0.011 W m−1 K−1, kz = 18.12 ± 1.15 W m−1 K−1. These results quantify the intrinsic anisotropy and thermal storage capacity essential for accurate modeling of cell heat transfer.
6.3. Accelerating rate calorimetry (ARC) testing
Thermal runaway behavior was evaluated using ARC under near-adiabatic conditions (Fig. 6(d)). During testing, the cell was subjected to incremental heating steps followed by isothermal hold periods until equilibrium was achieved. Once the self-heating rate exceeded a threshold of 0.02 °C min−1, the ARC automatically transitioned to adiabatic tracking, allowing real-time recording of temperature and pressure evolution. This procedure captured temperature-dependent self-heating rates, onset temperature, and maximum temperature rise, enabling the determination of intrinsic reactivity and heat generation rate Qgen(T). These results were later implemented as source terms in the numerical model for predictive simulation of thermal behavior.6.4. Experimental validation of the thermal safety boundary
To validate the simulation-derived thermal safety boundary, a convection-controlled experiment was conducted using a custom apparatus (Fig. 6(e)). The cell was mounted on a heating rack with heating wires to elevate the cell temperature and trigger self-heating. It should be noted that as the temperature raises, the exponential increase in internal chemical reaction heat generation becomes the dominant heat source, far exceeding the external heating input during the critical transition to thermal runaway. A Nidec fan supplied regulated air flow with a minimum velocity of 0.1 m s−1. Temperature evolution was monitored using the same Agilent data acquisition system.In each trial, external heating was terminated once the target temperature was reached, allowing the system to evolve under the competing effects of self-heating and convective cooling. The threshold temperature between stabilization and runaway was identified by progressively increasing the setpoint across successive tests. The maximum temperature attained in the last stable trial was recorded as the experimentally validated thermal safety temperature (Fig. S10 and S11).
6.5. Numerical modeling framework
A physics-based thermal model was developed to simulate heat transfer and predict the critical temperature for runaway initiation (Fig. 6(f)). The model represents the 18650 cell as a homogeneous cylinder with effective anisotropic properties. The transient heat transfer is governed by the energy conservation equation in cylindrical coordinates:
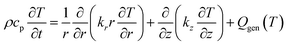 | (7) |
The boundary conditions are defined as follows. A convective heat transfer boundary condition is applied to the surfaces of the cell based on Newton's law of cooling:
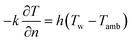 | (8) |
The simulation is initialized with a uniform temperature field:
| T(r,z,t = 0) = T0 | (9) |
The jellyroll was discretized into four layers, and temperature-dependent internal heat generation was implemented via interfacial heat source terms derived directly from the ARC data Qgen(T). The total heat release was spatially distributed to reflect volumetric reaction behavior while maintaining numerical stability. Heat conduction within the solid domain was coupled with convective boundary conditions on the cell surface, while the bottom face was treated as adiabatic. The initial temperature was prescribed uniformly.
Grid and time-step independence were verified. The model outputs, i.e., including peak temperature, temperature gradients, and critical temperature thresholds, served as the foundation for constructing the thermal safety boundary and calibrating the dimensionless thermal safety criterion.
Author contributions
Jiale Huang: methodology, simulation, data analysis, and writing – original draft; Yiyang Xia: experiment and data analysis; Shijia Xu: methodology and writing – review & editing; Ling Li: methodology and writing – review & editing; Hongbo Ji: experiment; Xiaoping Chen: conceptualization and methodology; Jun Xu: conceptualization, methodology, supervision, and writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ta09005a.Acknowledgements
XC was supported by National Natural Science Foundation of China (52575509).References
- Z. Rao, P. Lyu, M. Li, X. Liu and X. Feng, A thermal perspective on battery safety, Nat. Rev. Clean Technol., 2025, 1, 511–524, DOI:10.1038/s44359-025-00073-x.
- B. Liu, Y. Jia, C. Yuan, L. Wang, X. Gao, S. Yin and J. Xu, Safety issues and mechanisms of lithium-ion battery cell upon mechanical abusive loading: A review, Energy Storage Mater., 2020, 24, 85–112, DOI:10.1016/j.ensm.2019.06.036.
- X. Gao, C. Chak, Q. Hao, D. Zeng and J. Xu, Thermal safety of lithium-ion batteries: Mechanism, modeling, and characterizations, Annu. Rev. Heat Transfer, 2023, 26, 69–129, DOI:10.1615/AnnualRevHeatTransfer.2023048695.
- S. Sun and J. Xu, Safety behaviors and degradation mechanisms of aged batteries: A review, Energy Mater. Devices, 2024, 2, 9370048, DOI:10.26599/EMD.2024.9370048.
- Y. Liu, Y. Tian, Z. Fu, H. Du, B. Li, F. Kang, K. Amine and G. Chen, Thermite reaction-induced thermal runaway of lithium-ion batteries, Adv. Mater., 2025, e10486, DOI:10.1002/adma.202510486.
- Z. Cui and A. Manthiram, Thermal stability and outgassing behaviors of high-nickel cathodes in lithium-ion batteries, Angew. Chem., Int. Ed., 2023, 62, e202307243, DOI:10.1002/anie.202307243.
- L. Huang, G. Xu, X. Du, J. Li, B. Xie, H. Liu, P. Han, S. Dong, G. Cui and L. Chen, Uncovering LiH triggered thermal runaway mechanism of a high-energy LiNi0.5Co0.2Mn0.3O2/graphite pouch cell, Adv. Sci., 2021, 8, 2100676, DOI:10.1002/advs.202100676.
- Z. Zhong, L. Chen, C. Zhu, W. Ren, L. Kong and Y. Wan, Nano LiFePO4 coated Ni rich composite as cathode for lithium ion batteries with high thermal ability and excellent cycling performance, J. Power Sources, 2020, 464, 228235, DOI:10.1016/j.jpowsour.2020.228235.
- K. Chen, D. Zhang, J. Guo, F. Jiang, N. Shen, X. Yan, W. Zhang, N. Zhu, L. Chen, Y. Zhou, Z. Lyu, G. Xiao, X. Shen, X. Cheng and Y. Wu, Hydrogen generated from binders: An overlooked thermal runaway source in lithium-ion batteries, J. Energy Chem., 2025, 109, 602–608, DOI:10.1016/j.jechem.2025.06.004.
- H. Zhao, Y. Bai, H. Jin, J. Zhou, X. Wang and C. Wu, Unveiling thermal decomposition kinetics of single-crystalline Ni-rich LiNi0.88Co0.07Mn0.05O2 cathode for safe lithium-ion batteries, Chem. Eng. J., 2022, 435, 134927, DOI:10.1016/j.cej.2022.134927.
- Y. Wu, X. Liu, L. Wang, X. Feng, D. Ren, Y. Li, X. Rui, Y. Wang, X. Han, G. Xu, H. Wang, L. Lu, X. He, K. Amine and M. Ouyang, Development of cathode-electrolyte-interphase for safer lithium batteries, Energy Storage Mater., 2021, 37, 77–86, DOI:10.1016/j.ensm.2021.02.001.
- Y. Li, X. Feng, D. Ren, M. Ouyang, L. Lu and X. Han, Thermal runaway triggered by plated lithium on the anode after fast charging, ACS Appl. Mater. Interfaces, 2019, 11, 46839–46850, DOI:10.1021/acsami.9b16589.
- Z. Liu, Y. Jiang, Q. Hu, S. Guo, L. Yu, Q. Li, Q. Liu and X. Hu, Safer lithium-ion batteries from the separator aspect: Development and future perspectives, Energy Environ. Mater., 2021, 4, 336–362, DOI:10.1002/eem2.12129.
- W. Zhang, X. Feng, L. Lu, H. Wang, L. Wang, X. He, M. Wei and M. Ouyang, Anode failure hunter with a self-quenched function boosting lithium-ion battery safety, ACS Energy Lett., 2025, 10, 4933–4940, DOI:10.1021/acsenergylett.5c02364.
- Z. Jiang, C. Liu, L. Huang, S. Zhu, X. Zhang, R. Wu, T. Gong, Y. Wu, L. Guo, P. Han, J. Ma, G. Xu and G. Cui, Interfacial reactions take the lead: Elucidating the dominant role of cathode-electrolyte interactions in triggering thermal runaway of high-nickel lithium-ion batteries, Energy Environ. Sci., 2025, 18, 8232–8243, 10.1039/D5EE01431J.
- X. Ding, X. Wang, C. Zhu, J. Hu, M. Xu, M. Ma and J. Huang, Research on ignition criterion and combustion behavior of aluminum alloy for lithium battery, Sci. Rep., 2025, 15, 13734, DOI:10.1038/s41598-025-97209-7.
- X. Feng, M. Fang, X. He, M. Ouyang, L. Lu, H. Wang and M. Zhang, Thermal runaway features of large format prismatic lithium ion battery using extended volume accelerating rate calorimetry, J. Power Sources, 2014, 255, 294–301, DOI:10.1016/j.jpowsour.2014.01.005.
- X. Feng, D. Ren, S. Zhang, X. He, L. Wang and M. Ouyang, Influence of aging paths on the thermal runaway features of lithium-ion batteries in accelerating rate calorimetry tests, Int. J. Electrochem. Sci., 2019, 14, 44–58, DOI:10.20964/2019.01.14.
- Y. Wang, K. Zaghib, A. Guerfi, F. F. C. Bazito, R. M. Torresi and J. R. Dahn, Accelerating rate calorimetry studies of the reactions between ionic liquids and charged lithium ion battery electrode materials, Electrochim. Acta, 2007, 52, 6346–6352, DOI:10.1016/j.electacta.2007.04.067.
- J. Lamb, L. Torres-Castro, J. C. Hewson, R. C. Shurtz and Y. Preger, Investigating the role of energy density in thermal runaway of lithium-ion batteries with accelerating rate calorimetry, J. Electrochem. Soc., 2021, 168, 060516, DOI:10.1149/1945-7111/ac0699.
- S. Zheng, L. Wang, X. Feng and X. He, Probing the heat sources during thermal runaway process by thermal analysis of different battery chemistries, J. Power Sources, 2018, 378, 527–536, DOI:10.1016/j.jpowsour.2017.12.050.
- A. Kriston, I. Adanouj, V. Ruiz and A. Pfrang, Quantification and simulation of thermal decomposition reactions of Li-ion battery materials by simultaneous thermal analysis coupled with gas analysis, J. Power Sources, 2019, 435, 226774, DOI:10.1016/j.jpowsour.2019.226774.
- K. Nam, S. Bak, E. Hu, X. Yu, Y. Zhou, X. Wang, L. Wu, Y. Zhu, K. Chung and X. Yang, Combing in situ synchrotron X-ray diffraction and absorption techniques with transmission electron microscopy to study the origin of thermal instability in overcharged cathode materials for lithium-ion batteries, Adv. Funct. Mater., 2013, 23, 1047–1063, DOI:10.1002/adfm.201200693.
- C. Liu, S. Reed and A. Manthiram, Delineating the triphasic side reaction products in high-energy density lithium-ion batteries, Adv. Mater., 2025, e09889, DOI:10.1002/adma.202509889.
- X. Liu, L. Yin, D. Ren, L. Wang, Y. Ren, W. Xu, S. Lapidus, H. Wang, X. He, Z. Chen, G. Xu, M. Ouyang and K. Amine, In situ observation of thermal driven degradation and safety concerns of lithiated graphite anode, Nat. Commun., 2021, 12, 4235, DOI:10.1038/s41467-021-24404-1.
- Y. Jia, P. Zhao, D. P. Finegan and J. Xu, Dynamics of intra-cell thermal front propagation in lithium-ion battery safety issues, Adv. Energy Mater., 2024, 14, 2400621, DOI:10.1002/aenm.202400621.
- C. F. Lopez, J. A. Jeevarajan and P. P. Mukherjee, Experimental analysis of thermal runaway and propagation in lithium-ion battery modules, J. Electrochem. Soc., 2015, 162, A1905, DOI:10.1149/2.0921509jes.
- C. Jin, Y. Sun, J. Yao, X. Feng, X. Lai, K. Shen, H. Wang, X. Rui, C. Xu, Y. Zheng, L. Lu, W. Wang and M. Ouyang, No thermal runaway propagation optimization design of battery arrangement for cell-to-chassis technology, eTransportation, 2022, 14, 100199, DOI:10.1016/j.etran.2022.100199.
- H. Chen, J. E. H. Buston, J. Gill, D. Howard, R. C. E. Williams, E. Read, A. Abaza, B. Cooper and J. X. Wen, A simplified mathematical model for heating-induced thermal runaway of lithium-ion batteries, J. Electrochem. Soc., 2021, 168, 010502, DOI:10.1149/1945-7111/abd64c.
- A. Karmakar, H. Zhou, B. S. Vishnugopi, J. A. Jeevarajan and P. P. Mukherjee, State-of-charge implications of thermal runaway in Li-ion cells and modules, J. Electrochem. Soc., 2024, 171, 01529, DOI:10.1149/1945-7111/ad1ecc.
- C. Wu, M. Tang, W. Peng, A. Shi, S. Gao, S. Zhang and D. Wang, Study on the impact of temperature-dependent anisotropic thermal conductivity on thermal diffusion in lithium-ion batteries, J. Power Sources, 2024, 622, 235333, DOI:10.1016/j.jpowsour.2024.235333.
- X. Liu, T. Zhang, Q. Gao, Z. Han, H. Huang, Y. Xu, H. Chen and X. Xu, The suppression of thermal propagation using spray cooling with R410A in overheated lithium battery pack, Case Stud. Therm. Eng., 2024, 58, 104339, DOI:10.1016/j.csite.2024.104339.
- Y. Jia, M. Uddin, Y. Li and J. Xu, Thermal runaway propagation behavior within 18650 lithium-ion battery packs: A modeling study, J. Energy Storage, 2020, 31, 101668, DOI:10.1016/j.est.2020.101668.
- Y. Jia, B. Liu, Z. Hong, S. Yin, D. P. Finegan and J. Xu, Safety issues of defective lithium-ion batteries: identification and risk evaluation, J. Mater. Chem. A, 2020, 8, 12472–12484, 10.1039/D0TA04171H.
- J. Zhao, Z. Lv, D. Li, X. Feng, Z. Wang, Y. Wu, D. Shi, M. Fowler and A. Burke, Battery engineering safety technologies (BEST): M5 framework of mechanisms, modes, metrics, modeling, and mitigation, eTransportation, 2024, 22, 100364, DOI:10.1016/j.etran.2024.100364.
- J. Schoberl, M. Ank, M. Schreiber, N. Wassiliadis and M. Lienkamp, Thermal runaway propagation in automotive lithium-ion batteries with NMC-811 and LFP cathodes: Safety requirements and impact on system integration, eTransporation, 2024, 19, 100305, DOI:10.1016/j.etran.2023.100305.
- L. Wang, Y. Qiu, W. Yuan, Y. Tian and Z. Zhou, Next-generation battery safety management: Machine learning assisted life-time prediction and performance enhancement, J. Energy Chem., 2025, 109, 726–739, DOI:10.1016/j.jechem.2025.05.065.
- H. Moayedi, Performance improvement and thermal management of a lithium-ion battery by optimizing tab locations and cell aspect ratio, Int. J. Heat Mass Tran., 2023, 214, 124456, DOI:10.1016/j.ijheatmasstransfer.2023.124456.
- F. Zhang, X. Feng, C. Xu, F. Jiang and M. Ouyang, Thermal runaway front in failure propagation of long-shape lithium-ion battery, Int. J. Heat Mass Tran., 2022, 182, 121928, DOI:10.1016/j.ijheatmasstransfer.2021.121928.
- C. Mao, M. L. Wang, K. Gao, H. Jin, W. Y. Cho, H. Leon-Rodriguez, K. Hong, S. Han, J. Jeong and H. W. Kang, Dimensionless analysis and novel configuration for enhanced natural convection cooling in lithium-ion batteries, Case Stud. Therm. Eng., 2025, 74, 106766, DOI:10.1016/j.csite.2025.106766.
- D. Lee, J. Lee, J. Kim, S. Cho and C. Kim, Thermal behaviors analysis of 55 Ah large-format lithium-ion pouch cells with different cell aspect ratios, tab locations, and C-rates, Appl. Therm. Eng., 2020, 175, 115422, DOI:10.1016/j.applthermaleng.2020.115422.
- X. Feng, F. Zhang, J. Feng, C. Jin, H. Wang, C. Xu and M. Ouyang, Propagation dynamics of the thermal runaway front in large-scale lithium-ion batteries: Theoretical and experiment validation, Int. J. Heat Mass Tran., 2024, 225, 125393, DOI:10.1016/j.ijheatmasstransfer.2024.125393.
- D. Dubey, A. Mishra, S. Ghosh, M. Reddy and R. Pandey, Geometry-influenced cooling performance of lithium-ion battery, Appl. Therm. Eng., 2023, 230(Part A), 120723, DOI:10.1016/j.applthermaleng.2023.120723.
- G. Planinšič and M. Vollmer, The surface-to-volume ratio in thermal physics: From cheese cube physics to animal metabolism, Eur. J. Phys., 2008, 29, 369, DOI:10.1088/0143-0807/29/2/017.
- X. Yi, G. Qi, X. Liu, C. Depcik and L. Liu, Challenges and strategies toward anode materials with different lithium storage mechanisms for rechargeable lithium batteries, J. Energy Storage, 2024, 95, 112480, DOI:10.1016/j.est.2024.112480.
- Z. Wang, C. Xu, L. Chen, J. Si, W. Li, S. Huang, Y. Jiang, Z. Chen and B. Zhao, In-situ lithiation synthesis of nano-sized lithium sulfide/graphene aerogel with covalent bond interaction for inhibiting the polysulfides shuttle of Li-S batteries, Electrochim. Acta, 2019, 312, 282–290, DOI:10.1016/j.electacta.2019.04.169.
- S. Ko, H. Otsuka, S. Kimura, Y. Takagi, S. Yamaguchi, T. Masuda and A. Yamada, Rapid safety screening realized by accelerating rate calorimetry with lab-scale small batteries, Nat. Energy, 2025, 10, 707–714, DOI:10.1038/s41560-025-01751-7.
- J. Holman, Heat Transfer, McGraw-Hill, 10th edn, 2009 Search PubMed.
- N. Semenoff, Zur theorie des verbrennungsprozesses, Z. Phys., 1928, 48, 571–582, DOI:10.1007/BF01340021.
| This journal is © The Royal Society of Chemistry 2026 |