Effect of severe plastic deformation on thermoelectric properties of BiCuSeO
Gowtham
Venkatesan
a,
Srashti
Vishvakarma
b,
Inder
Kumar
b,
Satyam
Suwas
c and
Ramesh Chandra
Mallik
 *b
*b
aInter-disciplinary Centre for Energy Research, Indian Institute of Science, Bangalore 560012, India
bDepartment of Physics, Thermoelectric Material and Device Laboratory, Indian Institute of Science, Bangalore 560012, India. E-mail: rcmallik@iisc.ac.in
cDepartment of Materials Engineering, Texture and Related Studies Laboratory, Indian Institute of Science, Bangalore 560012, India
First published on 5th December 2025
Abstract
Severe plastic deformation processes are an excellent way to attain grain refinements and introduce dislocations in the material without compromising on the sample dimensions. High-pressure torsion (HPT) is a prime example of a severe plastic deformation process. In this work, HPT processing is employed to introduce a dense network of dislocation structures in BiCuSeO, which is a layered material known for its promising thermoelectric properties. Two categories of samples were prepared. The first category is the hot-pressed sample (HP) and the second category is the HPT-processed and subsequently hot-pressed samples (HPT-HP). The pristine HPT-HP1 sample shows a reduced bandgap of 0.74 eV compared to the pristine HP sample with a bandgap of 0.83 eV due to the combined effect of shear strain and pressure from the HPT process. This reduction in bandgap contributes to the increase in electrical conductivity from 17 S cm−1 in the pristine HP sample to 25 S cm−1 in the pristine HPT-HP1 sample at 823 K. The HPT-HP1 sample preparation conditions were then chosen to prepare a Cu-deficient Pb-substituted set of samples. The shear deformation from the HPT creates increased levels of dislocation density of about 5.02 × 1016 m−2 in the HPT-HP Bi0.94Pb0.06Cu0.97SeO sample compared to its HP counterpart (2.53 × 1014 m−2). These dislocations along with their corresponding lattice strains lead to a lattice part of thermal conductivity of 0.37 W m−1 K−1 at 823 K. Additionally, the reduced bandgap effect leads to an electrical conductivity of 145.5 S cm−1 in the HPT-HP Bi0.94Pb0.06Cu0.97SeO sample, resulting in a zT of 1.11 at 823 K.
1. Introduction
The global shift towards renewable energy resources is gaining momentum, with a growing recognition of the importance of even small-scale applications. In this context, thermoelectrics has emerged as a field of study, wherein waste heat is converted from various systems into electricity.1–4 A driving force behind this research is the ubiquity of the primary input waste heat, which is abundantly available in the surroundings at no additional cost. The thermoelectric measure of performance is characterized by the dimensionless figure of merit (zT) which is given by the relation: , where S is the absolute Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity comprising of the lattice part (κl) and electronic part (κe) and T is the absolute temperature.
, where S is the absolute Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity comprising of the lattice part (κl) and electronic part (κe) and T is the absolute temperature.
BiCuSeO, a p-type semiconductor thermoelectric material, distinguishes itself as an environment friendly material with noteworthy performance5 (zT ∼ 1.5 at 873 K) among thermoelectric materials.6 It has a tetragonal unit cell with a space group of P4/nmm (space group number - 129) where the origin has 2/m symmetry, and the 4mm symmetry is at the (¼, ¼, z) position.7 Its crystal structure follows a layered ZrCuSiAs-type arrangement containing two distinct layers – the (Bi2O2)2+ insulating layer and the (Cu2Se2)2− conducting layer.7,8 Being a layered material, it possesses inherently low thermal conductivity.7–10 Studies around the globe by various research groups have shown that the electrical properties of BiCuSeO could be improved as well.7,11–20 Recent studies on BiCuSeO ceramics have shown improvements in the performance of the material through reduction in lattice thermal conductivity with the help of dislocations.14,15 This work also attempts an approach toward implementing dislocations in the reduction of lattice thermal conductivity in BiCuSeO.
High-pressure torsion (HPT) is a severe plastic deformation (SPD) technique which is characterized by its strain inducing nature, to provide grain-refinement and dislocation density.16,17 In SPD, the volume of the sample is confined, and the material cannot escape or expand, for which HPT is a prime example.16 However, HPT as an SPD process is majorly used on metals17–19 which have the capacity to deform easily due to the presence of many active slip systems. Plastic deformation on ceramics is not extensively explored due to the brittle nature of ceramic materials.
This work utilizes HPT along with hot-pressing to compact and deform the BiCuSeO ceramic thereby introducing more dislocations than the hot-pressing technique without compromising on the sample's density (>96% relative density). Subsequently, Cu-deficient Pb-substituted BiCuSeO samples were also prepared using the same HPT-HP process. The Pb substituent was chosen due to the increase in carrier concentration it provides15,20–25 which would complement the reduction in thermal conductivity caused by the HPT-HP process. Cu-deficiency was chosen to further increase the carrier concentration since Cu vacancy is the primary source of p-type concentration in BiCuSeO.15,26 Dislocation densities of 5.02 × 1016 m−2 were achieved in the Bi0.94Pb0.06Cu0.97SeO HPT-HP sample, which results in a lattice thermal conductivity of 0.37 W m−1 K−1 and a respective zT of 1.11 at 823 K. This work unlocks a potential processing technique (HPT) for thermoelectric oxide materials to explore the reduction of lattice thermal conductivity and improve the thermoelectric performance.
2. Experimental
2.1. Synthesis
The synthesis of BiCuSeO involved measurements of constituent powders, each of 99.99% purity, including Bi2O3, Bi, Pb, Se, and Cu. These raw materials were weighed according to their stoichiometric ratio and then thoroughly mixed using an agate mortar and pestle to ensure a homogeneous blend. The mixed constituents were subsequently cold-compacted, resulting in the formation of small cylindrical structures. To maintain the purity of the samples, these cylinders were vacuum sealed in quartz tubes, creating a controlled environment with a pressure of approximately 10−3 mbar. A two-stage furnace heating schedule was implemented to synthesize the desired material ingot. In the first stage, the material was gradually heated to 573 K and maintained at this temperature for 12 hours. Subsequently, the second stage involved raising the temperature to 873 K and sustaining it for 24 hours, culminating in the formation of the target material ingot. The resulting ingot was then processed by manual grinding, yielding a fine powder. The fine powder was used for preparing two distinct categories of samples – the hot-pressed (HP) samples, and HPT followed by hot-pressing (HPT-HP) samples. All the samples prepared were compacted to a relative density >96%. The HPT parameters and the following hot-pressing parameters are tabulated in Table 1. The optimization process of HPT parameters is described in the SI, Table S1.| Composition | Temperature (K) | Pressure (MPa) | Pressing time (hours) | Nomenclature | Dislocation density (×1016 m−2) |
|---|---|---|---|---|---|
| a HPT conditions maintained – 0.88 GPa, 5 turns, 1 rpm | |||||
| BiCuSeO | 923 | 50 | 2 | HP | 0.0198 |
| BiCuSeO | 923 | 25 | 0.5 | HPT-HP1 | 3.4028 |
| BiCuSeO | 923 | 50 | 1 | HPT-HP2 | 2.5232 |
| BiCuSeO | 923 | 100 | 2 | HPT-HP3 | 2.4517 |
| Bi0.96Pb0.04Cu0.97SeO | 923 | 50 | 2 | Pb0.04 HP | 0.0322 |
| Bi0.94Pb0.06Cu0.97SeO | 923 | 50 | 2 | Pb0.06 HP | 0.0253 |
| Bi0.92Pb0.08Cu0.97SeO | 923 | 50 | 2 | Pb0.08 HP | 0.0164 |
| Bi0.96Pb0.04Cu0.97SeO | 923 | 25 | 0.5 | Pb0.04 HPT-HP | 5.0174 |
| Bi0.94Pb0.06Cu0.97SeO | 923 | 25 | 0.5 | Pb0.06 HPT-HP | 5.0246 |
| Bi0.92Pb0.08Cu0.97SeO | 923 | 25 | 0.5 | Pb0.08 HPT-HP | 4.9605 |
2.2. Preparation of HP samples
The material powder is loaded into a graphite die enclosed by two punches from the top and bottom. This setup is then loaded onto the vacuum hot-press machine, and the samples are prepared with the sintering conditions of 923 K, 50 MPa and 2 hours of pressing time (as shown in Table 1) while the system is continuously maintained at a vacuum of ∼10−6 mbar during the entire compaction process.2.3. Preparation of HPT-HP samples
The material powder is loaded into a stainless-steel cold compaction die of 12 mm diameter. The cold compaction was performed at 15 MPa for 7 minutes and the sample loaded into the HPT machine. The HPT sample (pellet after HPT processing) was then transferred to a graphite die for vacuum hot-pressing.2.4. Characterization
X-ray diffraction (XRD) measurements were carried out using a Rigaku SmartLab XRD instrument. The XRD data obtained were further subjected to Rietveld fitting, employing the pseudo-Voigt function to derive important parameters such as the Bragg-R factor, goodness of fit (χ2), and weighted-R factors. The peaks from the XRD plot were individually fit using the pseudo-Voigt function for the modified Williamson–Hall analysis. X-ray photoelectron spectra (XPS) were acquired utilizing a Kratos Axis Ultra system with an Al Kα (E = 1.487 eV) source, and the spectra were then analyzed with CasaXPS software. The room temperature band gap of the pellet samples was measured using Diffuse Reflectance Spectroscopy (DRS) in a PerkinElmer Lambda 900 UV/Vis/near-IR spectrometer in reflectance mode. The compositional quantification was performed by wavelength dispersive X-ray spectroscopy (WDS) using a JEOL JXA-8530 F instrument. Scanning electron microscopy (SEM) – secondary electron, backscattered electron imaging and electron back-scattered diffraction (EBSD) – was performed using a Zeiss Gemini-450 instrument. A Thermofisher FEI-Helios G4-UX instrument was used for the focused ion beam (FIB) milling of samples for transmission electron microscopy (TEM). The FIB parameters, like the excitation voltage, beam current, and exposure time, were optimized for the samples. Milling was done by Ga ions at 30 kV using 2.5 nA, 0.79 nA, 0.23 nA and 80 pA ion currents progressively, followed by cleaning at 5 kV and 24 pA to remove the high energy gallium, for getting lamellae as thin as 70 nm, which were subsequently used for TEM. An FEI-F30 instrument was employed to perform the TEM imaging at 300 k eV accelerating voltage. A TEM-FEI-TITAN instrument was used for performing the energy dispersive X-ray spectroscopy (EDS) and 4D-Scanning Tunneling Electron Microscopy (STEM) Strain Mapping of the TEM lamellae. The thermal diffusivity measurements were performed with a Linseis LFA-1000 instrument. The thermal conductivity (κ) was calculated using the relation κ = D × d × Cp, where D is the thermal diffusivity, d is the sample density and Cp is the specific heat capacity. The specific heat capacity was calculated to be the Dulong–Petit limit for each composition based on the Cp values of their corresponding precursors. The sample density d was measured using the Archimedes' principle measurement. The Seebeck coefficient and electrical resistivity measurements were done using the Linseis LSR-3 instrument through the temperature 300 K to 823 K. The error value in electrical resistivity and Seebeck coefficient data is 5%, and the error value in thermal conductivity data is 6%.3. Results & discussion
3.1. Optimization of BiCuSeO HPT-HP samples
 | ||
| Fig. 1 Room temperature X-ray diffraction (XRD) of (a) pristine BiCuSeO HP and HPT-HP samples, (b) XRD of the (102) peak displaying the peak broadening of BiCuSeO HP and HPT-HP pellets. | ||
 | ||
| Fig. 2 Rietveld refinement plot of the pristine BiCuSeO HPT-HP1 sample with fitting done using FullProf Suite software. | ||
Fig. 1b shows peak broadening of the (102) peak that occurs in the HPT sample which is due to refinement of grains during the HPT process. The broadened peaks of the HPT sample, after the HP process, i.e., in the HPT-HP samples, regain their original profile, shown by the reappearance of the (003) peak. This was confirmed by the modified Williamson–Hall (mWH) analysis wherein the dislocation density was calculated for the samples under study using the peak positions, and FWHM data of the peaks under study. The diffraction peaks observed in the samples were fitted with a pseudo-Voigt function individually to obtain the peak position (2θ) and the corresponding full width at half maximum (FWHM) (the parameters used in the calculation are given in the SI, Tables S4 and S5). The equation of the mWH plot is given in the following equation (eqn (1)).
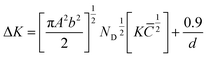 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ and ΔK = 2
θ/λ and ΔK = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(Δθ)/λ, where θ & λ are the angle of diffraction and the X-ray wavelength, b & d are the Burger vector magnitude and average grain size, respectively, and ND is the dislocation density. The ΔK versus
θ(Δθ)/λ, where θ & λ are the angle of diffraction and the X-ray wavelength, b & d are the Burger vector magnitude and average grain size, respectively, and ND is the dislocation density. The ΔK versus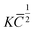 plot gives a slope which aids in calculating the dislocation density (tabulated in Table 1).14,27,28 The mWH plot quantifies the dislocation density by considering the size and strain components of peak broadening. The HPT sample had a dislocation density of 1.87 × 1017 m−2 whereas for the HP sample it was 1.97 × 1014 m−2. This difference is almost 3 orders of magnitude higher. Subsequently, the HPT-HP samples retain some dislocations created in the HPT process even after the HP densification. The values of dislocation density in the HPT-HP samples are still two orders of magnitude greater than those of the HP sample (Table 1).
plot gives a slope which aids in calculating the dislocation density (tabulated in Table 1).14,27,28 The mWH plot quantifies the dislocation density by considering the size and strain components of peak broadening. The HPT sample had a dislocation density of 1.87 × 1017 m−2 whereas for the HP sample it was 1.97 × 1014 m−2. This difference is almost 3 orders of magnitude higher. Subsequently, the HPT-HP samples retain some dislocations created in the HPT process even after the HP densification. The values of dislocation density in the HPT-HP samples are still two orders of magnitude greater than those of the HP sample (Table 1).
Fig. 4a and b show the EBSD microstructure maps of HP and HPT-HP1 samples, respectively. Compared to Fig. 4a, the EBSD maps in Fig. 4b are not properly indexed due to the microstructural straining which can also be observed in Fig. 3a. In Fig. 4b, multiple scans in the centre and edge regions of the HPT-HP1 sample were captured to observe the homogeneity of the grains in the microstructure after the HPT-HP process. Except the centre of the HPT-HP1 pellet (a region of about 100 microns), the grain size and microstructure are similar in the centre and at the edge region of the pellet, meaning that the HPT-HP process has resulted in a homogeneous microstructure.
3.1.4.1. Seebeck coefficient (S). The temperature dependent Seebeck coefficients (S) of HP and HPT-HP samples are displayed in Fig. 6a. There is a decrease in Seebeck coefficient observed for the HPT-HP samples compared to the HP sample. This decrease could be explained from the values of carrier concentration obtained from the hall measurement as shown in Table 2.
 | ||
| Fig. 6 Temperature dependent (a) absolute Seebeck coefficient (S), (b) electrical conductivity (σ), and (c) power factor of pristine BiCuSeO HP and HPT-HP samples. | ||
| Sample | Carrier concentration “p” (cm−3) at 300 K | Conductivity “σ” (S cm−1) at 300 K | Mobility “µ” (cm2 V−1 s−1) at 300 K | Reference |
|---|---|---|---|---|
| BiCuSeO | 1.9 × 1018 | — | 4.78 | Xu et al.15 |
| Bi0.94Pb0.06CuSeO | 7.89 × 1020 | — | 4.00 | |
| Pristine HP | 1.13 × 1018 | 1.46 | 8.07 | This work |
| Pristine HPT-HP1 | 7.63 × 1018 | 8.06 | 6.60 | |
| Pb0.06 HP | 5.71 × 1020 | 312.50 | 3.40 | |
| Pb0.06 HPT-HP | 8.00 × 1020 | 349.60 | 2.73 | |
| Pb0.08 HP | 1.68 × 1021 | 595.24 | 2.21 | |
| Pb0.08 HPT-HP | 1.72 × 1021 | 574.71 | 2.09 |
The increase in carrier concentration of the HPT-HP1 sample (7.63 × 1018 cm−3) compared to the HP sample (1.13 × 1018 cm−3) is due to the reduction in bandgap observed from UV-Vis spectroscopy. The Seebeck coefficient reduces since it is inversely proportional to the carrier concentration (p−2/3) as shown in eqn (2).
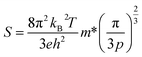 | (2) |
To summarize, according to the Hall measurement, there is an increase in carrier concentration and a decrease in mobility because of the HPT-HP process.
3.1.4.2. Electrical conductivity (σ). The temperature dependent electrical conductivity (σ) displayed in Fig. 6b shows an improvement in the HPT-HP samples as compared to the HP sample. The electrical conductivity can be described by eqn (3a)
| σ = peµ | (3a) |
The electrical conductivity of the HP sample is 17 S cm−1, and the values of HPT-HP1, HPT-HP2 and HPT-HP3 are 25.1 S cm−1, 24.8 S cm−1 and 24.2 S cm−1, respectively, at 823 K. This improvement is attributed to the increase in carrier concentration (p) resulting from the reduced bandgap, as shown in Table 2. Electrical conductivity is also affected by mobility, which is given by eqn (3b).
| µ = qτ/m* | (3b) |
Charge carrier mobility reduces in the HPT-HP1 sample (6.6 cm2 V−1 s−1) as compared to the HP sample (8.07 cm2 V−1 s−1). This could be due to the scattering of charge carriers by the defects introduced by the HPT-HP process. Despite the reduction in µ, electrical conductivity increases due to the dominant effect of carrier concentration.
3.1.4.3. Power factor (PF). Fig. 6c shows the temperature dependent power factor of the pristine HP and HPT-HP samples. The HPT-HP1 sample has a ∼30% increase in the power factor (0.35 mW m−1 K−2), as compared to the HP sample (0.27 mW m−1 K−2) at 823 K. Power factor is governed by the Seebeck coefficient and electrical conductivity. This improvement in power factor is driven by the increase in electrical conductivity in the HPT-HP samples as seen in Fig. 6b.
3.1.4.4. Thermal conductivity (κ). Fig. 7a shows the temperature dependent total thermal conductivity (κ) of the HP and HPT-HP samples. The HPT-HP samples exhibit lower thermal conductivity as compared to the HP sample. The κ value of the HP sample is 0.59 W m−1 K−1. This value is reduced to 0.49 W m−1 K−1, 0.51 W m−1 K−1 and 0.52 W m−1 K−1 for the HPT-HP1, HPT-HP2 and HPT-HP3 samples, respectively, at 823 K. Total thermal conductivity is a sum of the electronic part of thermal conductivity and the lattice part of thermal conductivity (eqn (4a)). The electronic part comes from the thermal conductivity contribution of the charge carriers (holes) (eqn (4b)), and it can be obtained by calculating the Lorenz number. Eqn (4c) was used for calculating the Lorenz number.34 The equations regarding the thermal conductivities are listed below in eqn (4a) and (4b).
| κ = κe + κl | (4a) |
| κe = LσT | (4b) |
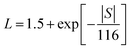 | (4c) |
 | ||
| Fig. 7 Temperature dependent (a) total thermal conductivity κ and (b) lattice thermal conductivity κl of the pristine BiCuSeO HP and HPT-HP samples. | ||
For the pristine HP sample, the value of κe is 0.02 W m−1 K−1 and κl is 0.57 W m−1 K−1. The electronic part of thermal conductivity in pristine BiCuSeO is an order of magnitude lower than the lattice part of thermal conductivity. So, the major contribution to the total thermal conductivity comes from the lattice part of thermal conductivity (κl). The Debye–Callaway model is employed to understand the effect of HPT-HP on the κl.
According to the Debye–Callaway model,35 the lattice part of thermal conductivity can be expressed as eqn (5),
 | (5) |
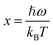 , θD is the Debye temperature, τT is the total relaxation time, ω is the angular frequency of the phonon, ℏ is the reduced Planck's constant, and νs is the average phonon velocity.
, θD is the Debye temperature, τT is the total relaxation time, ω is the angular frequency of the phonon, ℏ is the reduced Planck's constant, and νs is the average phonon velocity.
τ T can be calculated using Mattheissen's rule considering the scattering mechanisms using eqn (6),36
| τT−1 = τU−1 + τPD−1 + τGB−1 + τDc−1 + τDs−1 | (6) |
The lattice part of thermal conductivity, displayed in Fig. 7b, is governed by the above-mentioned scattering mechanisms, and the HPT makes a significant difference in the contributions from dislocations and grain boundaries. The contribution from Umklapp scattering, point defects, grain boundaries and dislocations can be described as equations eqn (7)–(11) shown below:14,37
| τGB−1 = vs/dg | (7) |
| τDis−1 = τcore−1 + τstrain−1 | (8) |
 | (9a) |
 | (9b) |
| τPD−1 = Aω4 | (10) |
 | (11) |
Fig. 8a shows the temperature dependent behaviour of κl at different temperatures for the HPT-HP1 sample. Till 623 K, κl ∝ T−0.58 and for T > 623 K, κl ∝ T−0.90. To understand the contribution from Umklapp scattering, point defects scattering, grain boundary scattering and dislocation scattering Debye–Callaway model fitting was employed (eqn (5)–(11)). Fig. 8b describes the contribution of different scattering mechanisms in the reduction of lattice thermal conductivity. The lattice thermal conductivity reduces with increasing temperature because with an increase in temperature, the Umklapp scattering becomes a majorly contributing phenomenon in the reduction of lattice thermal conductivity. The next major contribution comes from the point defects especially at the lower to intermediate temperature range, while at higher temperatures, the point defect contribution is relatively reduced. Additionally, due to the effect of HPT, there is a significant contribution from the grain boundary and dislocation scattering in the HPT-HP1 sample as displayed in Fig. 8b. The contributions from the dislocation scattering and the grain boundary scattering are notably high as compared to those in the HP sample displayed in Fig. S10, where the point defects and Umklapp scattering dominate.
Fig. 9a shows a grain with dislocations. Fig. 9b–d displays the strain maps (HPT-HP1 sample) generated using the diffraction patterns collected through 4D-STEM fitted with a TEM. The strain maps exhibit a spike in intensity in the regions that surround the dislocations observed in the BF image. The scattering contributions of the dislocations come from the core and strained regions, which are both dependent on the dislocation density. The dislocation densities of the samples are displayed in Table 1. From similar studies on the effects of dislocation strain, it has been shown that grain boundaries in the material are responsible for the scattering of lower range frequencies of phonons.14 The dislocations scatter mid to high frequency phonons, while the highest order frequencies are scattered by the point defects.14,38 Due to the severe plastic deformation provided by HPT, the grains are broken down to the sub-micron level, and from the TEM images, dense dislocations are observed (confirmed by the mWH calculation). These elements cumulatively work in reducing the lattice thermal conductivity of the material to 0.46 W m−1 K−1 in the HPT-HP1 sample at 823 K as shown in Fig. 7b. With the combined contributions from the lattice and electronic parts of thermal conductivities, a minimum total thermal conductivity of 0.49 W m−1 K−1 was observed for the HPT-HP1 sample at 823 K.
3.1.4.5. Figure of merit (zT). The temperature dependent dimensionless figure of merit (zT) is shown in Fig. 10. An improved zT of 0.58 was observed at 823 K for the HPT-HP1 sample, representing a 53% increase compared to the HP sample (zT = 0.38 at 823 K). The effect of severe plastic deformation in HPT-HP samples has helped in increasing the thermoelectric performance of the material by reducing the thermal conductivity and improving the power factor simultaneously, with the help of dislocations and strain-induced band structure alterations.
3.2. Pb substituted HPT-HP
The observations from Section 3.1 indicate that HPT processing improves the thermoelectric performance of BiCuSeO. To further improve the performance, Pb-substitution at the Bi site was employed. Pb substitution has been proven to enhance the carrier concentration in the BiCuSeO system.20–24,39 Additionally, Cu-deficiency is used to enhance the carrier concentration since Cu vacancies predominantly contribute to the p-type semiconducting nature of the material.40 From Section 3.1, the HPT-HP1 sample preparation conditions (0.88 GPa, 5 turns, 1 rpm for HPT; and 923 K, 25 MPa and 30 minutes for HP) were chosen for Pb-substitution. | ||
| Fig. 11 Room temperature XRD of (a) Pb-substituted BiCu0.97SeO, HP and HPT-HP samples, (b) XRD plot of the (102) peak displaying peak broadening and peak shift due to strain and Pb substitution. | ||
A pseudo-Voigt function was used to fit the individual peaks (tabulated in SI Table S3) to get the peak positions and FWHM values. These elements were used in calculating the dislocation density with the help of the modified Williamson–Hall (mWH) equation, as given in eqn (1). From this analysis, it is observed that dislocation densities of 5.02 × 1016 m−2 were achieved in the Pb0.06 HPT-HP sample. This is more than two orders of magnitude greater than the corresponding Pb0.06 HP sample which has a dislocation density of 2.5 × 1014 m−2. The dislocation densities of the samples in this section of the study are tabulated in Table 1.
 | (12) |
3.2.3.1. Seebeck coefficient (S). Fig. 13a shows the temperature dependent Seebeck coefficient of Cu-deficient Pb-substituted HP and HPT-HP samples. From Fig. 13a, it can be seen that the Seebeck coefficient decreases with an increase in Pb concentration. The decrease in S is attributed to the increase in carrier concentration due to Pb-substitution and Cu-deficiency as shown in Table 2. The carrier concentration of the Pb0.06 HP sample is 5.71 × 1020 cm−3, whereas that of the Pb0.08 HP sample is 1.68 × 1021 cm−3. This increase is reflected both in the HP and HPT-HP samples.
 | ||
| Fig. 13 Temperature dependent (a) absolute Seebeck coefficient (S), (b) electrical conductivity (σ), and (c) power factor of Pb-substituted BiCu0.97SeO HP and HPT-HP samples. | ||
There is a difference in Seebeck coefficient between the HP and HPT-HP samples for Pb0.04 and Pb0.06 compositions, and the Pb0.08 composition seems to be similar. The reason for the saturation is that, for the Pb0.08 composition, the HP and HPT-HP samples have a similar carrier concentration.
Although traces of secondary phases were found in the Pb0.06 HPT-HP and Pb0.08 HPT-HP samples as shown in Fig. S13, they were not detected in the XRD (Fig. 10). These secondary phases were identified to be Pb–Se secondary phases as shown in Fig. S14. Since the secondary phases were found in such scarce quantities, their effect on the transport properties of the material might be minimal.
3.2.3.2. Electrical conductivity (σ). The trend observed in the electrical conductivity is similar to that of the Seebeck coefficient, as shown in Fig. 13b. The electrical conductivity of the HPT-HP samples is increased for the Pb0.04 and Pb0.06 compositions in comparison to the HP samples, whereas for the Pb0.08 composition the difference is diminished. This can be correlated with the Hall measurement data showing a significant difference in carrier concentration between the HP and HPT-HP samples for the Pb0.06 composition. Meanwhile, the carrier concentration for the Pb0.08 composition is similar when comparing the HP (1.68 × 1021 cm−3) and HPT-HP (1.72 × 1021 cm−3) samples.
3.2.3.3. Power factor. The temperature dependent power factor of the Pb-substituted BiCu0.97SeO HP and HPT-HP samples is shown in Fig. 13c. The Pb-substituted samples exhibit a higher power factor as compared to the pristine one (Fig. 5c). The Pb0.08 HP sample shows the maximum power factor of 0.92 mW m−1 K−2, followed by the Pb0.06 HP sample with 0.85 mW m−1 K−2. The Pb0.04 HPT-HP, Pb0.06 HPT-HP and Pb 0.08 HPT-HP samples have power factors of 0.73 mW m−1 K−2, 0.77 mW m−1 K−2, and 0.84 mW m−1 K−2, respectively, at 823 K.
3.2.3.4. Thermal conductivity (κ). Fig. 14a shows the total thermal conductivity of the Pb-substituted HP and HPT-HP samples. The HPT-HP samples exhibit lower thermal conductivity as compared to the HP samples due to the severe plastic deformation process. The dislocation density observed from the XRD-mWH plot analysis (Table 1) is a major contributing factor to phonon scattering and low thermal conductivity. Thermal conductivity is in two parts – electronic and lattice thermal conductivity. The electronic part of thermal conductivity (Fig. S9) is increased as compared to that in Section 3.1, due to the high electrical conductivity of the Pb-substitution. The highest contribution to the electronic part of thermal conductivity is for the Pb0.08 samples, followed by the Pb0.06 and Pb0.04 samples, respectively. Fig. 14b displays the lattice thermal conductivities for the Pb-substituted HP and HPT-HP samples. The Pb-substituted HPT-HP samples have less lattice thermal conductivity compared to the Pb-substituted HP samples. This is because of the dislocation density, and the corresponding lattice strain according to eqn (7)–(9).
 | ||
| Fig. 14 Temperature dependent (a) thermal conductivity κ and (b) lattice thermal conductivity κl of Pb substituted BiCu0.97SeO HP and HPT-HP samples. | ||
The contribution of different scatterings to the lattice thermal conductivity was again studied using the Debye–Callaway model fitting (eqn (5)–(11)) for the Pb-substituted samples. Fig. 15 displays the different contributions to the reduction of temperature dependent lattice thermal conductivity. Similar to Section 3.1 (Fig. 8b), with the incorporation of HPT processing (HPT-HP), there is an increase in the contribution from grain boundary and dislocation scattering to the κl of the Pb0.06 HPT-HP sample shown in Fig. 15 compared to the Pb0.06 HP sample where the point defects and Umklapp scattering dominate as displayed in Fig. S11. In comparison to the pristine BiCuSeO HPT-HP1 sample, the value of the point defect prefactor (A) exhibits an increase. This is because of the Pb substitution and induced Cu vacancy in the material. Due to the increased effect of point defects in the Pb0.06 HPT-HP sample, as compared to the pristine HPT-HP1 sample, there is a reduction in the lattice thermal conductivity in the Pb0.06 HPT-HP sample. Additionally, the effect of point defects is dominant in the low to intermediate temperature range, while at the higher temperature range Umklapp scattering becomes more effective.
Fig. 16a shows the bright field image of a highlighted grain containing dislocations. Fig. 16b–d display the strain map showing the strain created around dislocations in a grain which has formed sub-grain like structures due to dislocation chaining or dislocation interlocking. Fig. 16a–d show that the dislocations affect the strain in their immediate neighbouring region. Also, when these dislocations form chains or sub-grains, it affects the entire grain's strain components. In addition, from the TEM images and discussions, pinning of dislocations is observed due to the point defect (Pb-substitution) enabled formation of Cottrel atmospheres.14 The lattice thermal conductivities of Pb0.04, Pb0.06 and Pb0.08 HPT-HP samples are 0.36 W m−1 K−1, 0.37 W m−1 K−1 and 0.40 W m−1 K−1, respectively, at 823 K. For a similar composition, these values are consistent with those of Ren et al.25 (∼0.4 W m K−1). From the TEM images in Section 3.1 (Fig. 3) and Section 3.2 (Fig. 12), it can be said that due to HPT processing, many dislocations were found in the lattice, and these dislocations are profoundly proliferated and clustered all over the microstructure. The movement of dislocation is inhibited due to dislocation pinning and the nature of the ceramic material.16 These dislocations also potentially exhibit the Orowan mechanism as shown in Fig. S3 in the SI. In the Orowan mechanism, dislocations bow around certain obstacles which are non-shearable.44 These dense clustered dislocations play a vital role in reducing the thermal conductivity of the material.
 | ||
| Fig. 16 4D-STEM strain mapping of a grain from Bi0.94Pb0.06Cu0.97SeO HPT-HP: (a) bright field image; (b) strain-xx component; (c) strain-yy component; (d) shear-xy component. | ||
3.2.3.5. Figure of merit (zT). The temperature dependent dimensionless figure of merit zT is plotted in Fig. 17a. The effect of HPT-HP on the Pb-substituted BiCu0.97SeO has improved the zT of the material. Comparing the HP and HPT-HP samples, the Pb0.04, Pb0.06 and Pb0.08 compositions each exhibit a 37%, 26% and 26% increase in the zT, respectively. The highest zT of 1.11 was achieved for the Pb0.06 HPT-HP sample at 823 K. A comparative plot of highest zT achieved in BiCuSeO is displayed in Fig. 17b from different literature reports.12,14,15,20,45–49
 | ||
| Fig. 17 (a) Temperature dependent dimensionless figure of merit zT of Pb substituted BiCu0.97SeO HP and HPT-HP samples, and (b) a comparison plot of the highest zT achieved in this work compared with BiCuSeO literature.12,14,15,20,45–49 | ||
4. Conclusion
In summary, this work focuses on achieving a high dislocation density through a severe plastic deformation process, i.e., high-pressure torsion (HPT). The effect of HPT resulted in a reduction in the bandgap of BiCuSeO from 0.83 eV in the HP sample to 0.74 eV in the HPT-HP1 sample. This reduction in bandgap led to an increased carrier concentration in the HPT-HP1, enhancing the electrical conductivity to 25.5 S cm−1 from 17 S cm−1 in the HP sample. The HPT-HP samples also show a reduction in thermal conductivity from 0.6 W m−1 K−1 in the HP sample to 0.49 W m−1 K−1 in the HPT-HP1 sample, because of increased dislocation density.To enhance thermoelectric performance, Pb substitution along with Cu deficiency was employed. The combined effect of Pb-substitution and Cu-deficiency increased the carrier concentration (5.71 × 1020 cm−3) by two orders of magnitude as compared to that of the pristine one (1.13 × 1018 cm−3). Dense dislocations introduced by the HPT process cause phonon scattering leading to a reduced κl value of 0.37 W m−1 K−1 in the Pb0.06 HPT-HP sample, resulting in a maximum zT of 1.11 at 823 K. This work demonstrates that high-pressure torsion is a viable and effective method of introducing dense dislocations while simultaneously reducing the bandgap for better thermoelectric properties in BiCuSeO.
Author contributions
G. V. did the conceptualization, methodology, all data acquisition, curation and formal analysis, wrote the original draft, and reviewed and edited the draft. S. V. helped with the review and editing of the draft. I. K. performed the Debye–Callaway model fitting for the lattice thermal conductivity. S. S. did the validation, visualization, funding acquisition, review and editing of the draft, and project administration. R. C. M. did the validation, visualization, funding acquisition, review and editing of the draft, and project administration.Conflicts of interest
There is no conflict of interest to declare.Data availability
The data that support the findings of this study are available in the manuscript and its supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ta07746j.Acknowledgements
The authors want to acknowledge SERB-DST (CRG/2022/000843-C) for providing financial support. The authors acknowledge the University Grant Commission (UGC), Government of India (ref: F.530/26/CAS-VI/2018(SAP-I)) for providing the thermal diffusivity measurement system (LFA 1000). The authors also want to acknowledge the Central Facility of the Department of Physics, Materials Engineering, Inorganic and Physical Chemistry, Solid-State Chemistry Unit, and the Advanced Facility for Microscopy and Microanalysis, Indian Institute of Science, Bengaluru.References
- S. Zhang, Z. Liu, X. Zhang, Z. Wu and Z. Hu, Innovation, 2024, 5, 100591 CAS.
- X. F. Zheng, C. X. Liu, Y. Y. Yan and Q. Wang, Renew. Sustain. Energy Rev., 2014, 32, 486–503 CAS.
- Y. Xiao and L. D. Zhao, Science, 2020, 367, 1196–1197 CrossRef CAS PubMed.
- H. Mamur, Ö. F. Dilmaç, J. Begum and M. R. A. Bhuiyan, Clean. Mater., 2021, 2, 100030 CrossRef CAS.
- Y. Liu, L. D. Zhao, Y. Zhu, Y. Liu, F. Li, M. Yu, D. B. Liu, W. Xu, Y. H. Lin and C. W. Nan, Adv. Energy Mater., 2016, 6, 1–9 Search PubMed.
- S. Tippireddy, P. K. D S, S. Das and R. C. Mallik, ACS Appl. Energy Mater., 2021, 4, 2022–2040 CrossRef CAS.
- L. D. Zhao, J. He, D. Berardan, Y. Lin, J. F. Li, C. W. Nan and N. Dragoe, Energy Environ. Sci., 2014, 7, 2900–2924 RSC.
- M. Li, N. Wang, S. Zhang, J. Hu, H. Xiao, H. Gong, Z. Liu, L. Qiao and X. Zu, J. Phys. D Appl. Phys., 2022, 55, 273002 CrossRef.
- B. Feng, X. Jiang, Z. Pan, L. Hu, X. Hu, P. Liu, Y. Ren, G. Li, Y. Li and X. Fan, Mater. Des., 2020, 185, 108263 CrossRef CAS.
- Z. Liu, X. Guo, R. Li, J. Qin, H. Li, X. Chen and X. Zhou, J. Mater., 2019, 5, 649–656 Search PubMed.
- S. Das, S. M. Valiyaveettil, K. H. Chen, S. Suwas and R. C. Mallik, Mater. Res. Express, 2019, 6, 086305 CAS.
- S. Das, A. Ramakrishnan, M. Rudra, K. H. Chen, T. P. Sinha, D. K. Misra and R. C. Mallik, J. Electron. Mater., 2019, 48, 3631–3642 CAS.
- Y. Liu, J. Ding, B. Xu, J. Lan, Y. Zheng, B. Zhan, B. Zhang, Y. Lin and C. Nan, Appl. Phys. Lett., 2015, 106, 233903 Search PubMed.
- Z. Yin, H. Zhang, Y. Wang, Y. Wu, Y. Xing, X. Wang, X. Fang, Y. Yu and X. Guo, Adv. Energy Mater., 2025, 15, 2403174 CAS.
- R. Xu, Z. Chen, Q. Li, X. Yang, H. Wan, M. Kong, W. Bai, N. Zhu, R. Wang, J. Song, Z. Li, C. Xiao and B. Ge, Research, 2023, 6, 1–10 Search PubMed.
- K. Edalati and N. Enikeev, Materials, 2024, 17(24), 6189 CAS.
- K. Edalati and Z. Horita, Acta Mater., 2011, 59, 6831–6836 CAS.
- D. Gunderov, A. Stotskiy, Y. Lebedev and V. Mukaeva, Metals, 2021, 11, 1–7 Search PubMed.
- M. Kawasaki, H. J. Lee, B. Ahn, A. P. Zhilyaev and T. G. Langdon, J. Mater. Res. Technol., 2014, 3, 311–318 CAS.
- S. Das, S. M. Valiyaveettil, K. H. Chen, S. Suwas and R. Chandra Mallik, AIP Adv., 2019, 9, 5–12 Search PubMed.
- F. Li, M. Ruan, Y. Chen, W. Wang, J. Luo, Z. Zheng and P. Fan, Inorg. Chem. Front., 2019, 6, 799–807 CAS.
- G. K. Ren, J. Le Lan, S. Butt, K. J. Ventura, Y. H. Lin and C. W. Nan, RSC Adv., 2015, 5, 69878–69885 CAS.
- L. Pan, D. Bérardan, L. Zhao, C. Barreteau and N. Dragoe, Appl. Phys. Lett., 2013, 102, 023902 CrossRef.
- B. Feng, G. Li, Z. Pan, Y. Hou, C. Zhang, C. Jiang, J. Hu, Q. Xiang, Y. Li, Z. He and X. Fan, Mater. Lett., 2018, 217, 189–193 CrossRef CAS.
- G. K. Ren, S. Wang, Z. Zhou, X. Li, J. Yang, W. Zhang, Y. H. Lin, J. Yang and C. W. Nan, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- D. H. Kim, H. Y. Hong, J. K. Lee, S. D. Park and K. Park, J. Mater. Res. Technol., 2020, 9, 16202–16213 CrossRef CAS.
- T. Ungár, I. Dragomir, Á. Révész and A. Borbély, J. Appl. Crystallogr., 1999, 32, 992–1002 CrossRef.
- S. K. Saha and G. Dutta, Phys. Rev. B, 2016, 94, 1–8 Search PubMed.
- S. López-moreno, J. Sánchez-martín, E. Bandiello, M. Bettinelli, C. L. Bull, C. J. Ridley and D. Errandonea, J. Phys. Chem. Solids, 2023, 183, 111604 CrossRef.
- B. G. Kim, J. Korean Phys. Soc., 2021, 79, 946–952 CrossRef CAS.
- P. Sahoo, M. J. Sneha, B. P. Mandal and A. Dixit, Mater. Lett., 2022, 324, 132747 CrossRef CAS.
- D. Wan, S. Bai, S. Fan, X. Xiang, Z. Li, Y. Liu, P. Kang, L. Zheng, L. D. Zhao and H. Xu, Nat. Commun., 2025, 16, 6284 CAS.
- L. Huang, Z. Chen and J. Li, RSC Adv., 2015, 5, 5788–5794 CAS.
- H. S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506 Search PubMed.
- J. Callaway and H. C. Von Baeyer, Phys. Rev., 1960, 120, 1149–1154 CAS.
- Y. Yu, S. Zhang, A. M. Mio, B. Gault, A. Sheskin, C. Scheu, D. Raabe, F. Zu, M. Wuttig, Y. Amouyal and O. Cojocaru-Mirédin, ACS Appl. Mater. Interfaces, 2018, 10, 3609–3615 CAS.
- I. Kumar, J. Peter, G. Shankar, P. Pambannan, S. Suwas, R. K. Biswas and R. C. Mallik, Phys. Rev. B, 2024, 110, 1–16 Search PubMed.
- H. S. Kim, S. D. Kang, Y. Tang, R. Hanus and G. Jeffrey Snyder, Mater. Horizons, 2016, 3, 234–240 CAS.
- Z. Zhou, Y. Huang, B. Wei, Y. Yang, D. Yu, Y. Zheng, D. He, W. Zhang, M. Zou, J. Lan, J. He, C. Nan and Y. Lin, Nat. Commun., 2013, 14, 2410 Search PubMed.
- Y. Liu, L. D. Zhao, Y. Liu, J. Lan, W. Xu, F. Li, B. P. Zhang, D. Berardan, N. Dragoe, Y. H. Lin, C. W. Nan, J. F. Li and H. Zhu, J. Am. Chem. Soc., 2011, 133, 20112–20115 CAS.
- M. Arakelyan, OALib, 2018, 05, 1–11 Search PubMed.
- S. Kiyohara, T. Tsuru and Y. Kumagai, Sci. Technol. Adv. Mater., 2024, 25, 1–9 Search PubMed.
- D. Setman, E. Schafler, E. Korznikova and M. J. Zehetbauer, Mater. Sci. Eng., A, 2008, 493, 116–122 Search PubMed.
- S. M. Hafez Haghighat and R. Schäublin, Philos. Mag. Lett., 2013, 93, 575–582 CAS.
- A. Novitskii, I. Serhiienko, S. Novikov, Y. Ashim, M. Zheleznyi, K. Kuskov, D. Pankratova, P. Konstantinov, A. Voronin, O. A. Tretiakov, T. Inerbaev, A. Burkov and V. Khovaylo, ACS Appl. Energy Mater., 2022, 5, 7830–7841 CAS.
- L. Jiang, L. Han, C. Lu, S. Yang, Y. Liu, H. Jiang, Y. Yan, X. Tang and D. Yang, ACS Appl. Mater. Interfaces, 2021, 13, 11977–11984 CrossRef CAS PubMed.
- J. Sui, J. Li, J. He, Y. L. Pei, D. Berardan, H. Wu, N. Dragoe, W. Cai and L. D. Zhao, Energy Environ. Sci., 2013, 6, 2916–2920 RSC.
- Y. Liu, J. Lan, W. Xu, Y. Liu, Y. L. Pei, B. Cheng, D. B. Liu, Y. H. Lin and L. D. Zhao, Chem. Commun., 2013, 49, 8075–8077 RSC.
- H. Kang, J. Li, Y. Liu, E. Guo, Z. Chen, D. Liu, G. Fan, Y. Zhang, X. Jiang and T. Wang, J. Mater. Chem. C, 2018, 6, 8479–8487 RSC.
| This journal is © The Royal Society of Chemistry 2026 |








