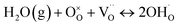Phase diagrams and chemical expansion upon hydration of proton conductors BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_n (0 ≤ x ≤ 0.8; 0 ≤ n ≤ 0.1)

Abstract

Proton-conducting ceramics are promising candidates for applications in sustainable energy technologies, with BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (BZCYYb) perovskites standing out as excellent proton conductors. However, comprehensive structural studies of these materials, particularly concerning their hydrated and dehydrated states, as well as the effects of composition (x) and temperature, are still limited. This study explores the crystal structures of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_n and BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) using neutron and X-ray diffraction techniques. The chemical expansion due to water incorporation is quantified by measuring unit cell volumes via X-ray diffraction, showing strong agreement with mass loss data from thermogravimetric analysis (TGA). Phase diagrams for both hydrated and dehydrated phases are developed, revealing a decrease in symmetry and a reduction in phase transition temperatures as x increases. Hydration notably affects octahedral tilting, as evidenced by comparisons of hydrated and dehydrated structures at room temperature (RT). Furthermore, a bond valence sum (BVS)-based approach is proposed, offering improved predictions of octahedral tilting and structural stability compared to the traditional Goldschmidt tolerance factor. These structural insights, particularly the influence of hydration, are essential for advancing our understanding of these materials and providing a solid foundation for linking their structure to their properties.

---

1. Introduction

Since the discovery in 2010 of the proton-conducting perovskite BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9 (BZCYYb1711), which exhibits both high protonic conductivity and enhanced chemical stability, this material has emerged as a benchmark electrolyte for protonic ceramic fuel cells (PCFCs) and protonic ceramic electrolysis cells (PCECs).¹ To date, more than 230 publications, according to the Web of Science, have investigated this compound and related compositions within the BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 family.^2–9

The high proton conductivity of these oxides stems from their ability to incorporate protons via a hydration reaction. In humid atmospheres, water molecules react with oxygen vacancies and lattice oxygen to form hydroxyl groups, according to the reaction:

This results in hydrated compositions that can be written as BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9−n□_0.1−n(OH)_2n (0 ≤ n ≤ 0.1), which reflects the consumption of n lattice oxygens and the formation of 2n hydroxyl groups. An alternative formulation, BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9□_0.1−n(H₂O)_n (0 ≤ n ≤ 0.1), more clearly illustrates water incorporation without implying lattice oxygen removal. For simplicity, the latter notation, BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_n, omitting explicit reference to the oxygen vacancy, will be used consistently throughout this manuscript.

These materials adopt the perovskite ABO₃ structure, with Ba occupying the A-site and Zr, Ce, Y, and Yb substituting on the B-site. The mismatch in ionic radii between A- and B-site cations induces structural distortions via cooperative tilting of the BO₆ octahedra, resulting in symmetry lowering from the ideal cubic structure. Due to the low X-ray scattering factor of oxygen, subtle superlattice reflections associated with octahedral tilting are often undetectable by X-ray diffraction. In contrast, neutron diffraction is highly effective in detecting such symmetry changes due to its sensitivity to both cations and oxygen.

We recently reported on an intermediate composition, BaZr_0.4Ce_0.4Y_0.1Yb_0.1O_2.9 (BZCYYb4411), which exhibits enhanced chemical stability as a result of its higher Zr/Ce ratio.^10,11 That study explored three sintering strategies, two of which successfully reduced the sintering temperature from 1600 °C to 1400 °C, enabling one-step synthesis and sintering while preserving high ionic conductivity.

In an earlier neutron diffraction study, we investigated BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9 and identified a tetragonal I4/mcm structure at RT, with a transition to the cubic Pm3̄m phase around 650 °C.¹² At the time, the material was assumed to be in a dry state, as no deliberate hydration was performed. However, subsequent thermogravimetric analysis (TGA) and additional diffraction studies revealed that these materials readily absorb moisture during synthesis or sintering, resulting in hydrated states.

Given the strong link between hydration state and proton conductivity, we conducted a systematic investigation of the BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 series, with explicit consideration of hydration effects. The specific objectives of this study are:

• To determine the crystal structures of both fully hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 at RT via neutron diffraction and as a function of temperature via X-ray diffraction, as well as the fully dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 compounds (0 ≤ x ≤ 0.8) under the same conditions, using neutron data as a structural reference;

• To correlate mass changes upon dehydration, as measured by TGA, with unit cell volume changes observed by X-ray diffraction, thereby isolating the chemical expansion effect associated with water uptake;

• To determine the thermal expansion coefficients (TECs) of both hydrated and dehydrated samples, revealing the effects of hydration and the Zr/Ce ratio on TEC values;

• To compare the RT structures of hydrated and dehydrated materials to assess the structural impact of hydration;

• To construct phase diagrams for both hydrated and dehydrated members of the BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 series, identifying key phase transitions;

• Finally, to introduce a new predictive approach based on bond valence sum (BVS) calculations, which incorporates the effects of oxygen vacancies and provides more accurate insights into octahedral tilting and phase stability than the traditional Goldschmidt tolerance factor.

2. Experimental

2.1 Powder synthesis

Nine compositions of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) were synthesized via the glycine–nitrate process (GNP), following procedures reported previously.^10,12 Stoichiometric amounts of the corresponding metal nitrates were employed. The as-synthesized nanoparticles were collected, manually ground in an agate mortar, and subsequently pressed into pellets. To prevent interaction with the crucible and to compensate for possible Ba evaporation, powders of identical composition were used as both a bedding layer and a covering medium during sintering. The pellets were sintered in air at 1600 °C for 1 h, cooled to room temperature, and polished to remove any superficial surface layer. For thermogravimetric analysis (TGA), X-ray diffraction, and neutron diffraction measurements, the pellets were ground into fine powders and stored in closed glass vials under ambient conditions until use. Under these conditions, the samples reacted with atmospheric moisture, indicative of hydrated phase formation, which was subsequently confirmed to be fully hydrated by TGA and neutron diffraction.

2.2 Characterization techniques

2.2.1 Thermogravimetric analysis (TGA). TGA measurements were conducted on approximately 170 mg of hydrated BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9 powder using a STA449F5 Jupiter instrument (NETZSCH) under a flowing argon atmosphere (Alphagaz 1 grade, Air Liquide; pH₂O < 6 × 10⁻⁴ atm) with a heating rate of 5 °C min⁻¹.

2.2.2 Neutron powder diffraction. Neutron powder diffraction patterns were collected on the D2B high-resolution diffractometer at the Institut Laue-Langevin (ILL), Grenoble, France, at RT. Samples with x = 0, 0.1, 0.2, 0.3, and 0.4 were placed inside vanadium cans and measured under vacuum conditions (10⁻⁴–10⁻⁵ mbar). Data were recorded over a 2θ range of 0–160° with a step size of 0.05°, using a wavelength of 1.59440 Å. Each pattern was collected over a 3-hour period.

2.2.3 X-ray powder diffraction. Temperature-dependent X-ray diffraction (XRD) measurements of hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) were carried out using a Bruker D8 Advance diffractometer equipped with a high-temperature HTK 1200N chamber. Measurements were performed in Bragg–Brentano geometry with Cu-Kα radiation (λ₁ = 1.5406 Å, λ₂ = 1.54439 Å) and a Vantec detector. The 2θ range was 10°–130°, with a step size of 0.017° and a counting time of 1.95 s per step. Heating and cooling were carried out at a rate of 6 °C min⁻¹.

Two types of experimental series were conducted:

• All nine compositions were examined under nitrogen (U-grade, Air Liquide; pH₂O < 10⁻³ atm) from RT to 1000 °C, with one scan recorded every 100 °C. The first pattern corresponds to the fully hydrated phase at RT.

• Seven compositions (x = 0, 0.1, 0.2, 0.3, 0.4, 0.6, and 0.8) were studied under dynamic vacuum (∼1–5 × 10⁻⁵ mbar), from 1000 °C down to RT, with one scan recorded every 100 °C. These conditions are standard for achieving water-free states and for preventing rehydration during cooling. The final pattern corresponds to the fully dehydrated phase at RT.

For both neutron and X-ray powder diffraction, Rietveld refinements were performed using Jana2006 software.¹³ More accurate standard deviations of refined parameters were obtained using the Bérar and Lelann corrections.¹⁴ Error bars for structural parameters were plotted considering standard deviations, obtained after the Bérar correction, multiplied by a factor of 3.

3. Results and discussion

3.1 Evidence for water incorporation

Fig. 1 presents the TGA curve of the as-prepared BZCYYb1711 sample (x = 0.1), conducted from RT to 1000 °C under a nitrogen atmosphere. A mass loss begins near 300 °C and ends around 900 °C, resulting in a total weight reduction of ∼0.6%. This thermal behavior, typical of proton-conducting ceramic phases, is attributed to the release of incorporated water.^15–19 In the compound BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9, full hydration corresponds to complete occupation of oxygen vacancies by oxygen from incorporated water, yielding BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9(H₂O)_0.1. The theoretical mass loss associated with full dehydration is 0.56%, which is in close agreement with the measured ∼0.6%, confirming that the as-prepared BZCYYb1711 is fully hydrated. In Fig. 1, the mass loss is also expressed as the number of incorporated water molecules per formula unit, denoted n, with n = 0.1 representing the fully hydrated state.

Fig. 1 (a) Thermogravimetric analysis (TGA) of as-prepared BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9(H₂O)_0.1 under flowing argon at a heating rate of 5 °C min⁻¹. (b) Temperature dependence of the unit cell volumes of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (x = 0.2, 0.4, 0.5, 0.6) during two heat treatments from RT to 1000 °C under nitrogen (first heating: red; second heating: black).

Further evidence for water incorporation is provided by X-ray thermodiffraction, performed on as-prepared BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 samples with x = 0.2, 0.4, 0.5, and 0.6 under a nitrogen atmosphere (Fig. 1). During the first heat treatment, data were collected every 100 °C from RT to 1000 °C (red markers). After cooling to RT, a second heat treatment was conducted under identical conditions (black markers). The pseudo-cubic subcell volume is plotted as a function of temperature. At low temperatures, the linear increase in cell volume reflects the thermal expansion of the hydrated phase, from which the thermal expansion coefficient (TEC) can be extracted (see Section 3.3.3).

Deviations from linearity, observed at ∼500 °C for x = 0.2 and ∼400 °C for x = 0.4–0.6, mark the onset of dehydration. The cell volume contracts and then increases again up to ∼800 °C, after which a new linear trend emerges, corresponding to the thermal expansion of the fully dehydrated phase. Similar behavior has been reported in other proton-conducting ceramics, including BaIn_0.8Ti_0.2O_2.6,¹⁵ BaZr_0.8Y_0.2O_3−δ,²⁰ BaZr_1−xY_xO_3−δ (x = 0.05, 0.1, 0.2) and BaCe_0.8Y_0.2O_3−δ,²¹ BaZr_1−xY_xO_3−δ (x = 0.1, 0.15, 0.2, 0.25 and 0.3),²² BaZr_0.7Ce_0.2O_0.1O_3−δ,²³ BaZr_0.9Y_0.1O_3−δ and BaZr_0.7Ce_0.2Y_0.1O_3−δ,²⁴ BaZr_xCe_0.8−xY_0.2O_3−δ (0 ≤ x ≤ 0.8),²⁵ BaZr_xCe_0.8−xY_0.1Yb_0.1O_3−δ (x = 0.1, 0.4),²⁶ and BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_3−δ.²⁷

Upon cooling, rehydration occurs to varying degrees. For x = 0.6, the RT cell volume matches that of the extrapolated dehydrated phase, indicating minimal rehydration. For x = 0.2, the volume suggests a fully hydrated state, while intermediate compositions (x = 0.4, 0.5) exhibit partial rehydration. The degree of rehydration is related to the basicity of the samples, which depends on the Zr/Ce ratio (see Section 3.3.2). Between RT and 300 °C, the cell volume increases, approaching the expansion behavior of the hydrated phase. From 400 °C to 800 °C, a more rapid volume decrease is observed during the second heat treatment, again indicative of dehydration. Above 800 °C, all samples exhibit the thermal expansion behavior characteristic of the dehydrated phase, consistent with the first run.

Throughout these experiments, the X-ray chamber was continuously flushed with nitrogen, and no external water vapor was introduced. Hence, rehydration is attributed to residual moisture in the N₂ gas or chamber environment, which, although limited, was sufficient to induce partial rehydration. This facile hydration motivated us to investigate the structure of the dehydrated phases under vacuum to ensure truly water-free conditions.

Since the x = 0.1 as-prepared sample is confirmed to be fully hydrated by TGA, and all samples were prepared under identical conditions, it is reasonable to assume that all as-prepared samples are initially fully hydrated. This assumption will be further confirmed by neutron diffraction data collected on the as-prepared samples.

3.2 Structural characterization by neutron diffraction

The structures of the as-prepared samples with compositions x = 0, 0.1, 0.2, 0.3, and 0.4 were investigated by neutron diffraction at RT. Neutron diffraction is particularly well-suited for resolving octahedral tilt systems in perovskite structures due to its sensitivity to oxygen positions, enabling accurate determination of tilt patterns that may be difficult to detect using X-ray diffraction alone. Fig. 2 shows the neutron diffraction patterns of these hydrated samples.

Fig. 2 (a) Rietveld-refined neutron diffraction patterns for hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (x = 0, 0.1, 0.2, 0.3, 0.4) at RT; (b) enlarged view highlighting characteristic diffraction peaks; and (c) corresponding octahedral tilts derived from the refinements.

The tolerance factor (t), defined as t = (r_A + r_O)/√2(r_B + r_O), where r_A, r_B, and r_O are the ionic radii of the A-site cation, B-site cation, and oxygen anion, respectively, is a reliable predictor of octahedral tilting in perovskite structures. The ideal cubic perovskite (unit cell a_p × a_p × a_p) exhibits no octahedral tilting (Glazer tilt system a⁰a⁰a⁰), typically observed when t ≈ 1. As the B-site ionic radius increases, t decreases, leading to less favorable B–O bonding and promoting cooperative BO₆ octahedral tilting to accommodate the structural mismatch.

Fifteen space groups have been identified to describe all known tilt systems.²⁸ A double perovskite unit cell (2a_p × 2a_p × 2a_p) is commonly used to facilitate the interpretation of diffraction patterns. In addition to the main reflections, with all even Miller indices, superlattice reflections of mixed parity, arising from structural distortions such as tilting, can appear. These reflections are often weak in X-ray diffraction but are more readily observed with neutrons.

For the BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 system, the tolerance factor increases from 0.936 (x = 0) to 0.989 (x = 0.8). In a previous study, we reported that the x = 0.1 sample (t = 0.943) crystallizes in the tetragonal I4/mcm space group, corresponding to the a⁰a⁰c⁻ tilt system.¹² For lower t values (x = 0), the symmetry is expected to be the same or lower, while higher t values (x > 0.1) favor increased symmetry as t approaches 1.

3.2.1 Structure of x = 0.1. For x = 0.1, tetragonal distortion is evident from the splitting of h00 reflections (e.g., 400), while hhh reflections (e.g., 222) remain unsplit (Fig. 2b). Superlattice reflections with odd–odd–odd Miller indices, indicative of anti-phase octahedral tilting, are also observed. Structural refinement in the I4/mcm space group yielded the best fit, supported by acceptable reliability factors and fewer refined parameters compared to the monoclinic I2/m model.¹² Notably, the intense 311 and 313 superlattice reflections (2θ ≈ 35.33° and 46.62°) correspond to the 211 and 213 reflections in the I4/mcm setting. These results confirm that the corner-sharing BO₆ octahedra are tilted about the [001] direction, consistent with the a⁰a⁰c⁻ tilt system. Tilt angles were calculated from the refined atomic coordinates and are presented in Table 1 and Fig. 2c.

Table 1 Selected crystallographic parameters obtained from Rietveld refinements of neutron diffraction data recorded at RT for hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (x = 0, 0.1, 0.2, 0.3, 0.4). Hydrogen atoms were not localized

Composition		x = 0.0	x = 0.1	x = 0.2	x = 0.3	x = 0.4
Space group		I2/m	I4/mcm	I4/mcm	I4/mcm	I4/mcm
Tilt system		a ^0 b ^− c ^−	a ^0 a ^0 c ^−	a ^0 a ^0 c ^−	a ^0 a ^0 c ^−	a ^0 a ^0 c ^−
a (Å)		6.2371(6)	6.1478(2)	6.12442(18)	6.1122(3)	6.0999(4)
b (Å)		8.7250(8)	6.1478(2)	6.12442(18)	6.1122(3)	6.0999(4)
c (Å)		6.2536(5)	8.8789(5)	8.8273(4)	8.7434(8)	8.6423(12)
β (°)		91.267(6)	90	90	90	90
V (Å^3)		340.23(5)	335.58(2)	331.10(2)	326.64(4)	321.57(5)
a red (Å)		4.4103(4)	4.34715(14)	4.33062(13)	4.3219(2)	4.3133(3)
b red (Å)		4.3625(4)	4.34715(14)	4.33062(13)	4.3219(2)	4.3133(3)
c red (Å)		4.4219(3)	4.4395(2)	4.4136(2)	4.3417(4)	4.3212(6)
V red (Å^3)		85.057(12)	83.895(5)	82.775(5)	81.66(2)	80.393(13)
c/a		1.00265(12)	1.02123(6)	1.01917(5)	1.01150(10)	1.00182(15)
c/b		1.01363(12)	—	—	—	—
a/b		1.01096(13)	—	—	—	—
φ (°) [001]		12.09	11.6621(4)	10.7358(4)	9.2243(6)	7.6772(8)
φ′ (°) [010]		4.44	—	—	—	—
Ba	Wyckoff position	4i	4b	4b	4b	4b
	x	0.249(5)	0	0	0	0
	y	0	0.5	0.5	0.5	0.5
	z	0.746(3)	0.25	0.25	0.25	0.25
	SOF	1	1	1	1	1
	U eq (Å^2)	0.021(4)	0.0239(14)	0.0257(12)	0.0243(17)	0.021(3)
Ce/Zr/Y/Yb	Wyckoff position	4e	4c	4c	4c	4c
	x	0.25	0	0	0	0
	y	0.25	0	0	0	0
	z	0.25	0	0	0	0
	SOF Ce/Zr/Y/Yb	0.8/0.0/0.1/0.1	0.7/0.1/0.1/0.1	0.6/0.2/0.1/0.1	0.5/0.3/0.1/0.1	0.4/0.4/0.1/0.1
	U eq (Å^2)	0.0115(11)	0.0121(11)	0.0122(9)	0.0141(12)	0.014(2)
O1	Wyckoff position	4i	4a	4a	4a	4a
	x	0.212(3)	0	0	0	0
	y	0	0	0	0	0
	z	0.1737(18)	0.25	0.25	0.25	0.25
	SOF	1	1	1	1	1
	U eq (Å^2)	0.031(4)	0.0329(15)	0.0311(13)	0.0305(19)	0.026(3)
O2	Wyckoff position	4g	8h	8h	8h	8h
	x	0	0.1984(4)	0.2026(4)	0.2094(6)	0.2163(8)
	y	0.3001(15)	0.6984(4)	0.7026(4)	0.7094(6)	0.7163(8)
	z	0	0	0	0	0
	SOF	1	1	1	1	1
	U eq (Å^2)	0.021(4)	0.0311(8)	0.0328(9)	0.0362(14)	0.038(2)
O3	Wyckoff position	4h	—	—	—	—
	x	0.5	—	—	—	—
	y	0.270(2)	—	—	—	—
	z	0	—	—	—	—
	SOF	1	—	—	—	—
	U eq (Å^2)	0.029(4)	—	—	—	—
R-Factors	R p (%)	1.90	3.22	2.66	3.67	2.85
	R wp (%)	2.42	4.03	3.51	4.81	3.75
	R obs (%)	2.32	3.22	2.67	4.18	3.23
	χ ^2	1.43	1.64	1.49	1.63	2.05

---

3.2.2 Structure of x = 0.0. The neutron diffraction pattern of the x = 0 sample shows the same key reflections as x = 0.1, but with noticeable peak shoulders (Fig. 2b). Rietveld refinements were conducted in both I4/mcm and I2/m space groups. Superior reliability factors were obtained with the I2/m model: R_p = 1.94%, R_wp = 2.47%, R_obs = 2.51%, and GoF = 1.47 (44 refined parameters), versus R_p = 2.39%, R_wp = 3.17%, R_obs = 3.71%, and GoF = 1.88 (28 refined parameters) in I4/mcm. The shoulder adjacent to the 311 reflection corresponds to the splitting of the 311 superlattice reflection in the I2/m space group, which remains unsplit in the I4/mcm setting. Therefore, the Rietveld refinement was successfully performed in the I2/m space group, characterized by the tilt system a⁰b⁻c⁻. Tilt angles, determined geometrically by analyzing planes defined by four oxygen atoms in corner-sharing octahedra, are 12.09° around [001] and 4.44° around [010] (Fig. 2c).

3.2.3 Structure of x = 0.2, 0.3, and 0.4. The diffraction patterns of x = 0.2 and x = 0.3 exhibit the same tetragonal distortion features as x = 0.1: h00 reflections are split, hhh reflections remain unsplit, and superlattice reflections are present. For x = 0.4, the splitting of h00 reflections becomes less distinct; however, the tetragonal symmetry persists, supported by the continued presence of superlattice peaks. Rietveld refinements for x = 0.2–0.4 were successfully conducted in the I4/mcm space group (Table 1).

3.2.4 Oxygen occupancy. Refinements of atomic positions and displacement parameters were performed for all five compositions (x = 0–0.4). The oxygen site occupancies (a_i) for O1(4i), O2(4g), and O3(4h) in the I2/m space group, and O1(4a) and O2(8h) in the I4/mcm space group, were initially fixed at 0.967 to account for oxygen vacancies in BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9. Subsequently, free refinement of oxygen occupancy yielded the following values:

• x = 0: 1.02(2), 1.08(4), 1.030(18)

• x = 0.1: 1.000(16), 1.012(12)

• x = 0.2: 0.992(16), 1.008(12)

• x = 0.3: 0.992(3), 0.996(16)

• x = 0.4: 1.02(5), 0.99(4)

These values approach full oxygen occupancy (1.000), deviating significantly from the nominal 0.967. Final refinements assumed full occupancy, indicating that oxygen vacancies have been filled by oxygen from incorporated water. This interpretation is consistent with TGA data showing full hydration of the as-prepared samples. The resulting empirical formula is BaZr_xCe_0.8−xY_0.1Yb_0.1O₃ (x = 0–0.4), which corresponds to BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 when hydrogen is considered. Tables 1 and S1 summarize the results of the Rietveld refinements.

3.2.5 Evolution of tetragonal distortion with composition. As the zirconium content (x) increases from 0.1 to 0.4, a progressive reduction in tetragonal distortion is observed. This evolution is evidenced by four key parameters: the intensity of superlattice reflections, the c/a ratio, the octahedral tilt angle φ, and the spontaneous tetragonal strain e_t¹² (Fig. 3).

Fig. 3 Composition dependence of the integrated intensity of the 311 and 313 reflection peaks, the c/a ratio, the tilt angle (φ), and the tetragonal strain (e_t) for hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (x = 0, 0.1, 0.2, 0.3, 0.4).

First, the intensities of the 311 and 313 superlattice reflections decrease progressively with increasing x, indicating a reduction in octahedral tilting. Second, the 400 and 004 diffraction peaks move closer together, tending to merge, which reflects a convergence of the lattice constants and a decreasing c/a ratio. The tetragonal distortion is quantified using the reduced perovskite cell parameters, with a = a_t/√2 and c = c_t/2. Although the c/a ratio decreases as x increases, it remains greater than 1 at x = 0.4, confirming the persistence of tetragonal symmetry.

Third, the tilt angle φ, extracted from the refined structural parameters, decreases from 11.6621(4)° at x = 0.1 to 7.6772(8)° at x = 0.4, further corroborating the reduction in structural distortion. Finally, the spontaneous tetragonal strain e_t also decreases with increasing x.

At x = 0.5, the Goldschmidt tolerance factor t approaches unity, and the structure is best described by the cubic space group Pm3̄m (see Section 3.3). The tetragonal-to-cubic phase transition as a function of composition was analyzed by plotting the composition dependence of e_t. The data were fitted to the equation 0 = a(x_t − x) + be_t + ce_t² where x_t is the critical composition at which the symmetry change occurs.²⁹ The fit yields x_t = 0.41, confirming that the x = 0.4 sample retains tetragonal symmetry, while the x = 0.5 sample adopts the cubic phase. The I4/mcm-to-Pm3̄m phase transition, driven by increasing tolerance factor t, is consistent with behavior observed in analogous systems such as SrTi_xZr_1−xO₃,³⁰ Sr_1−xBa_xZrO₃,³¹ and Sr_1−xCa_xTi_0.5Mn_0.5O₃.³²

In summary, increasing Zr content raises the tolerance factor t, while the tetragonal distortion, as reflected by superlattice reflection intensity, c/a ratio, tilt angle φ, and tetragonal strain e_t, decreases. These findings provide a comprehensive structural framework for interpreting the behavior of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) as a function of temperature, to be investigated further using X-ray diffraction under nitrogen and vacuum atmospheres.

3.3 Thermodiffraction of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) in N₂ atmosphere

The nine as-prepared samples discussed herein are fully hydrated, as confirmed in the preceding section. As these samples were obtained from different synthesis batches, minor discrepancies between cell parameters derived from neutron and X-ray diffraction may occur. However, these discrepancies are negligible compared to the compositional differences between successive samples.

Due to the weak intensity or absence of superlattice reflections in X-ray diffraction patterns, phase identification cannot rely solely on their presence. Instead, the splitting behavior of the h00, hh0, and hhh main reflections is used to determine the appropriate space group. Based on previous neutron diffraction results, three candidate space groups are considered: I2/m, I4/mcm, and Pm3̄m, with reflection splitting behaviors as follows:

• h00 reflections: split into 3, 2, and 1 peaks for I2/m, I4/mcm, and Pm3̄m, respectively.

• hh0 reflections: split into 4, 2, and 1 peaks, respectively.

• hhh reflections: split into 2, 1, and 1 peaks, respectively.

This analysis enables reliable identification of the structural symmetry.

Fig. S1 presents the full X-ray diffraction patterns across a broad 2θ range for each composition as a function of temperature. Fig. 4a highlights the 400 reflection (representative of h00) for all compositions from RT to 1000 °C. At RT, increasing Zr content (x) shifts the 400 peak to higher 2θ values, consistent with substitution of larger Ce⁴⁺ by smaller Zr⁴⁺ cations. Upon heating, no consistent shift toward lower 2θ is observed due to competing thermal and chemical expansion effects, leading to an atypical cell volume evolution.

Fig. 4 (a) Temperature dependence of the 400 peak for all nine compositions of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_n (0 ≤ x ≤ 0.8; 0 ≤ n ≤ 0.1) under nitrogen, recorded on heating from RT to 1000 °C (M = monoclinic; T = tetragonal; C = cubic). Evolution of the characteristic 440 and 444 peaks for (b) x = 0 and (c) x = 0.2 at selected temperatures.

At RT, the 400 peak splitting diminishes with increasing x and eventually becomes a single peak at a composition to be discussed later. Neutron data confirm I2/m symmetry for the hydrated x = 0.0 sample, which is also used for X-ray refinement. Fig. 4b shows the 440 (hh0) and 444 (hhh) reflections for x = 0 at 25 °C, 500 °C, and 600 °C. At 500 °C, the 444 reflection remains split, consistent with I2/m symmetry, while at 600 °C all splitting disappears, indicating a transition to the cubic Pm3̄m phase. Consequently, Rietveld refinements were performed using I2/m from RT to 500 °C and Pm3̄m from 600 °C onward. This unusual I2/m → Pm3̄m transition has also been reported in BaZr_0.3Ce_0.5Y_0.2O_3−δ and BaZr_0.2Ce_0.6Y_0.2O_3−δ.²⁵

For x = 0.2, the 400 and 440 reflections are split at RT, whereas the 444 reflection is not (Fig. 4a and c), consistent with I4/mcm symmetry. By 500 °C, all splitting vanishes, indicating a transition to the cubic phase. Rietveld refinements used I4/mcm from RT to 400 °C and Pm3̄m from 500 to 1000 °C. A similar I4/mcm → Pm3̄m transition was also observed for x = 0.1 and corroborated by literature.¹²

Fig. 5 shows the temperature dependence of the reduced cell volume, reduced cell parameters, and c/a ratio for each composition. For x = 0.1–0.4, the c/a ratio is used to determine the tetragonal-to-cubic (I4/mcm → Pm3̄m) transition temperature. The tetragonal phase is characterized by c/a > 1; with increasing temperature, the distortion diminishes and c/a approaches unity. When the ratio reaches 1 within error, the phase is considered cubic.

Fig. 5 Temperature dependence of the cell volume, cell parameters, and the c/a ratio for hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_n (0 ≤ x ≤ 0.8; 0 ≤ n ≤ 0.1) under nitrogen. c/a ratio calculated in the tetragonal I4/mcm space group to identify the tetragonal-to-cubic transition (see text).

Only the x = 0 sample exhibits an I2/m → Pm3̄m transition. Samples with x = 0.1–0.4 undergo an I4/mcm → Pm3̄m transition, with the transition temperature decreasing as x increases. For x = 0.5–0.8, no structural transition is observed; these samples retain cubic symmetry across the entire 25–1000 °C range, as supported by the c/a ratio of approximately 1.

As shown in Section 3.1, which details four representative compositions, the evolution of the pseudo-cubic subcell volume with temperature follows a similar trend for all samples (Fig. 5). At low temperatures, linear expansion corresponds to hydrated phases, from which the thermal expansion coefficient (TEC) is derived (see Section 3.3.3). Deviation from linearity above ∼300 °C indicates the onset of dehydration. The unit cell volume decreases until ∼600 °C, then increases up to ∼800 °C, after which a new linear regime is observed, corresponding to the thermal expansion of the fully dehydrated phase.

For compositions with RT cubic symmetry (x = 0.5–0.8), the reduced cell parameter tracks the unit cell volume. In contrast, for lower-symmetry compositions, the a and c parameters evolve nonlinearly with temperature and converge at the phase transition. Exceptions include x = 0.1 and x = 0.2, where a increases and c decreases nonlinearly before converging at the transition point.

Room-temperature cell volumes, parameters, and structural details for the hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) compounds are presented in Table 2.

Table 2 Space group, cell parameters, cell volumes, corresponding pseudo-cubic subcell parameters and volumes, c/a ratio, and Goldschmidt tolerance factor (t) for all nine hydrated compositions of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) at RT under nitrogen, as determined by X-ray diffraction

Composition	Space group	Cell parameters (Å)				Cell volume (Å^3)	Subcell parameters (Å)			c red/ared	Subcell volume (Å^3)	t
		a	b	c	β		a red	b red	c red
x = 0.0	I2/m	6.2303(6)	8.7245(6)	6.2492(5)	91.179(6)	339.61(5)	4.4055(4)	4.3622(3)	4.4188(3)	—	84.884(12)	0.936
x = 0.1	I4/mcm	6.1493(5)	6.1493(5)	8.8627(9)	90	335.13(5)	4.3482(3)	4.3482(3)	4.4313(4)	1.01912(13)	83.782(12)	0.943
x = 0.2	I4/mcm	6.12181(10)	6.12181(10)	8.8216(2)	90	330.602(11)	4.32877(7)	4.32877(7)	4.4108(1)	1.01895(2)	82.650(2)	0.949
x = 0.3	I4/mcm	6.1188(5)	6.1188(5)	8.6890(12)	90	325.32(6)	4.3266(3)	4.3266(3)	4.3445(6)	1.00413(16)	81.330(15)	0.955
x = 0.4	I4/mcm	6.1011(4)	6.1011(4)	8.6556(10)	90	322.19(5)	4.3141(2)	4.3141(2)	4.3278(5)	1.00317(10)	80.547(12)	0.962
x = 0.5	Pm3̄m	4.29678(13)	4.29678(13)	4.29678(13)	90	79.329(4)	—	—	—	1	79.329(4)	0.968
x = 0.6	Pm3̄m	4.27560(15)	4.27560(15)	4.27560(15)	90	78.161(5)	—	—	—	1	78.161(5)	0.975
x = 0.7	Pm3̄m	4.2568(2)	4.2568(2)	4.2568(2)	90	77.133(7)	—	—	—	1	77.133(7)	0.982
x = 0.8	Pm3̄m	4.2350(2)	4.2350(2)	4.2350(2)	90	75.953(6)	—	—	—	1	75.953(6)	0.989

---

3.3.1 Chemical expansion due to hydration. For the fully hydrated BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9(H₂O)_0.1 composition, TGA was correlated with the temperature-dependent unit cell volume, measured under nitrogen from RT to 1000 °C. In Fig. 6a, the linear thermal contributions from both the low-temperature hydrated and high-temperature dehydrated phases (dotted lines) were subtracted from the total volume data (black points), yielding ΔV values (blue points) that isolate the volume expansion due solely to hydration.¹⁵

Fig. 6 (a) Chemical expansion (ΔV = V_total − V_thermal) due to hydration in BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9(H₂O)_n. (b) Correlation between chemical expansion and the number of water molecules, n(H₂O), incorporated in BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_2.9(H₂O)_n. (c) Chemical expansion due to hydration in BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_n (0 ≤ x ≤ 0.8).

Fig. 6b compares the ΔV curve with the water content n(H₂O), derived from TGA. The near-perfect overlap between ΔV and n(H₂O) confirms that chemical expansion is directly attributable to proton incorporation. Similar analyses across all compositions are summarized in Fig. 6c, showing that water incorporation into BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 results in an average volume increase of 0.70(13) ų. This corresponds to approximately 7 ų per water molecule. In comparison, proton-conducting BaTi_xIn_1−xO_2.5+x/2 (x < 0.25) exhibits a slightly lower volume increase upon hydration, less than 7 ų per water molecule, indicating good agreement with the values obtained in this study.³³

3.3.2 Influence of Zr/Ce ratio on basicity and dehydration behaviour. The temperature at which dehydration occurs decreases with increasing x: it is approximately 500 °C for x = 0, 0.1, and 0.2; around 400 °C for x = 0.3, 0.4, and 0.5; approximately 300–400 °C for x = 0.6; and around 300 °C for 0.7 and 0.8. This decrease in dehydration temperature is attributed to changes in the basicity of the material. The tendency of the material to react with water vapor is governed by its basicity, which is influenced by the electronegativity of its constituent cations. Since the electronegativity of Ce⁴⁺ (χ = 1.412) is lower than that of Zr⁴⁺ (χ = 1.476),³⁴ the basicity of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 decreases as x increases, thereby explaining the lower dehydration temperatures observed at higher Zr content. A similar correlation between decreasing dehydration temperature and decreasing basicity has been reported in other systems. For instance, in BaZr_xCe_0.8−xY_0.2O_3−δ (0 ≤ x ≤ 0.8), basicity decreases with increasing x,¹⁵ and in BaTi_xIn_1−xO_2.5+x/2 (0.2 ≤ x ≤ 0.6), basicity also decreases with increasing x, in accordance with the electronegativity of the cations.²⁵

3.3.3 Thermal expansion coefficient in N₂ atmosphere. In PCFCs, PCECs, and oxide fuel cells, a mismatch in thermal expansion coefficients (TECs) between electrolyte and electrode layers can induce mechanical stresses, cracks, or delamination. Selecting materials with minimal TEC differences is critical to avoid these issues. TECs were calculated for the hydrated phases based on the low-temperature linear regions of the unit cell volume vs. temperature data. TECs were extracted from the slope of linear fits to plots of (ΔV/V)/3 versus temperature (K), as shown in Table 3. A clear trend is observed: the TEC decreases with increasing Zr content, from 13.5 × 10⁻⁶ K⁻¹ at x = 0 to 8.9 × 10⁻⁶ K⁻¹ at x = 0.8.

Table 3 Thermal expansion coefficients for hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) in N₂ and for dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) in vacuum

	TEC (×10^−6 K^−1) in N2	TEC (×10^−6 K^−1) in vacuum
x = 0	13.5 (25–400 °C)	14.2 (25–200 °C)	11.2 (500–1000 °C)
x = 0.1	12.9 (25–400 °C)	11.7 (25–200 °C)	9.1 (500–1000 °C)
x = 0.2	12.5 (25–400 °C)	8.6 (25–1000 °C)
x = 0.3	14.0 (25–300 °C)	7.8 (25–1000 °C)
x = 0.4	12.1 (25–300 °C)	8.5 (25–1000 °C)
x = 0.5	11.4 (25–400 °C)	—
x = 0.6	11.5 (25–300 °C)	8.2 (25–1000 °C)
x = 0.7	10.3 (25–300 °C)	—
x = 0.8	8.9 (25–300 °C)	7.5 (25–1000 °C)

---

3.4 Thermodiffraction of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) in vacuum

Following the characterization of phase transitions and chemical expansion in hydrated samples, the dehydrated samples were analyzed to assess their thermal and structural behavior. Dehydration was achieved by heating the compounds to 1000 °C under vacuum conditions, ensuring complete removal of incorporated water. Thermodiffraction experiments were subsequently conducted during cooling from 1000 °C to RT, with XRD patterns collected at 100 °C intervals under vacuum (Fig. S2). The final diffraction pattern corresponds to the fully dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 compositions at RT.

As with the hydrated series, phase identification and symmetry assignments were based on the careful analysis of peak splitting in the main reflections rather than relying exclusively on superlattice reflections. This approach provided a more reliable assessment of symmetry changes and transition points.

Fig. 7a presents the evolution of the 400 reflection for seven compositions as a function of temperature. At RT, the 400 peak shifts progressively to higher 2θ values with increasing zirconium content, consistent with the smaller ionic radius of Zr⁴⁺ relative to Ce⁴⁺, a trend also observed in the hydrated samples. During cooling from 1000 °C to RT, all compositions exhibit a continuous and linear shift of the 400 reflection toward higher 2θ values, which is characteristic of pure thermal contraction in the absence of hydration-induced structural distortions.

Fig. 7 (a) Temperature dependence of the 400 peak for seven compositions of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) in vacuum, recorded on cooling from 1000 °C to RT (M = monoclinic; T = tetragonal; C = cubic). (b) Evolution of the characteristic 440 and 444 peaks for (b) x = 0 and (c) x = 0.4 at selected temperatures.

For the x = 0 composition, the 444 reflection is split at RT, indicating monoclinic symmetry (space group I2/m; see Fig. 7b). As temperature increases, the monoclinic unit cell parameters gradually converge, approaching a higher symmetry near the phase transition (Fig. 8). At 500 °C, the splitting of the 444 peak is no longer resolved, and successful Rietveld refinement was achieved in the tetragonal I4/mcm space group. At 800 °C, the error bar of the c/a ratio intersects unity, justifying a cubic structure assignment and refinement in the Pm3̄m space group. A similar structural evolution was observed for the x = 0.1 composition.

Fig. 8 Temperature dependence of the cell volume, cell parameters, and c/a ratio for dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) under vacuum. c/a ratio calculated in the tetragonal I4/mcm space group to identify the tetragonal-to-cubic transition (see text).

In all compositions where monoclinic symmetry was not detected at RT, the c/a ratio was calculated to differentiate between tetragonal and cubic phases. For example, the x = 0.4 sample exhibits c/a < 1 at RT, yet refinement across the entire temperature range, from RT to 1000 °C, was performed in the Pm3̄m cubic space group. In cases where a tetragonal-to-cubic transition (I4/mcm → Pm3̄m) was suspected, the c/a ratio was plotted against temperature to determine the point at which it approached unity. Rietveld refinements were conducted in the appropriate space group based on these criteria.

For compositions with x = 0.4 to 0.8, no symmetry change was detected throughout the entire temperature range; these samples retained cubic symmetry (Pm3̄m) from 1000 °C down to RT.

The temperature dependence of the unit cell volume for the dehydrated samples exhibits linear behavior for compositions that remain cubic (x = 0.4, 0.6, and 0.8; similar behavior is inferred for x = 0.5 and 0.7), as illustrated in Fig. 8. For samples with lower Zr content (x = 0 to 0.3), slight deviations from linearity are observed near the transition points. These deviations, however, are considerably smaller than those seen in the hydrated samples. This nearly linear dependence of the cell volume on temperature indicates the absence of chemical expansion, further confirming that rehydration did not occur, resulting in fully dehydrated phases. As temperature increases, the lattice parameters expand and converge smoothly, indicating continuous thermal expansion toward the transition temperatures.

The unit cell volumes, lattice parameters, and refined structural parameters for the dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 compounds at RT are summarized in Table 4.

Table 4 Space group, cell parameters, unit cell volumes, corresponding pseudo-cubic subcell parameters and volumes, c/a ratios, and Goldschmidt tolerance factors (t) for seven dehydrated compositions of BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (x = 0, 0.1, 0.2, 0.3, 0.4, 0.6, and 0.8) at RT under vacuum, as determined by X-ray diffraction

Composition	Space group	Cell parameters (Å)				Cell volume (Å^3)	Subcell parameters (Å)			c red/ared	Subcell volume (Å^3)	t
		a	b	c	β		a red	b red	c red
x = 0.0	I2/m	6.20664(17)	8.76090(15)	6.22860(13)	90.0725(19)	338.685(13)	4.38876(12)	4.38045(7)	4.40429(9)	—	84.671(3)	0.936
x = 0.1	I2/m	6.1797(13)	8.7182(9)	6.2029(7)	90.122(15)	334.19(9)	4.3697(9)	4.3591(4)	4.3861(4)	—	83.54(2)	0.943
x = 0.2	I4/mcm	6.12181(10)	6.12181(10)	8.8216(2)	90	330.01(14)	4.3511(4)	4.3511(4)	4.3580(15)	1.0016(3)	82.50(3)	0.949
x = 0.3	I4/mcm	6.1278(4)	6.1278(4)	8.6775(18)	90	325.84(7)	4.3330(2)	4.3330(2)	4.3387(9)	1.0013(2)	81.460(17)	0.955
x = 0.4	Pm3̄m	4.31297(11)	4.31297(11)	4.31297(11)	90	80.228(4)	—	—	—	1	80.228(4)	0.962
x = 0.6	Pm3̄m	4.27104(9)	4.27104(9)	4.27104(9)	90	77.911(3)	—	—	—	1	77.911(3)	0.975
x = 0.8	Pm3̄m	4.22638(13)	4.22638(13)	4.22638(13)	90	75.493(4)	—	—	—	1	75.493(4)	0.989

---

3.4.1 Thermal expansion coefficients in vacuum. Thermal expansion coefficients (TECs) were determined from the linear regions of the unit cell volume vs. temperature plots, using the same methodology applied to the hydrated samples measured under a nitrogen atmosphere (see Table 2). Under vacuum conditions, TECs are consistently higher at lower temperatures. For example, TECs range from 14.2 × 10⁻⁶ K⁻¹ (x = 0) to 11.7 × 10⁻⁶ K⁻¹ (x = 0.1) in the low-temperature range. At elevated temperatures, these values decrease to 11.2 × 10⁻⁶ K⁻¹ (x = 0) and 9.1 × 10⁻⁶ K⁻¹ (x = 0.1), respectively.

As observed for the hydrated samples, the thermal expansion coefficient systematically decreases with increasing zirconium content. Specifically, TEC values drop from 14.2 × 10⁻⁶ K⁻¹ for x = 0 to 7.5 × 10⁻⁶ K⁻¹ for x = 0.8. This trend aligns with literature reports for related systems, such as BaZr_xCe_0.8−xY_0.2O_3−δ (0.2 ≤ x ≤ 0.7), in which TECs were also found to decrease with increasing Zr content, from 11.3 × 10⁻⁶ K⁻¹ (x = 0.2) to 8.4 × 10⁻⁶ K⁻¹ (x = 0.7).³⁵

Finally, with the exception of x = 0, the TECs of hydrated phases are systematically higher than those of their dehydrated counterparts. A similar trend has been reported for fully hydrated BaIn_0.8Ti_0.2O_2.6(H₂O)_0.4 (TEC = 14.1 × 10⁻⁶ K⁻¹) compared to its dehydrated form, BaIn_0.8Ti_0.2O_2.6 (TEC = 12.5 × 10⁻⁶ K⁻¹).¹⁵

3.5 Structural variations in hydrated and dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9: composition dependence and hydration effects at room temperature

Fig. 9, compiled from data reported in Tables 2 and 4, presents the composition dependence at RT of the unit cell volume, lattice parameters, and c/a ratio for fully hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 and dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 compounds, as determined by X-ray diffraction.

Fig. 9 Composition dependence of the unit cell volume, cell parameters, and c/a ratio at RT for hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) under nitrogen and dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) under vacuum.

A linear contraction of the unit cell volume with increasing Zr content is observed, reflecting the substitution of larger Ce⁴⁺ ions (0.87 Å, sixfold coordination) with smaller Zr⁴⁺ ions (0.72 Å). As previously discussed in the Section 3.2.5, for compositions exhibiting tetragonal symmetry, increasing Zr content results in a reduction of tetragonal distortion, characterized by a decreasing c/a ratio. Since the c/a ratio directly correlates with the octahedral tilt angle, this trend enables a meaningful comparison of tilt angles between hydrated and dehydrated phases.

For compositions with monoclinic symmetry, three ratios, c/a, a/b, and c/b, were derived from the reduced cell parameters. For x = 0, the average of these three ratios is 1.0086 for the hydrated phase, significantly higher than that of the dehydrated counterpart (1.0036). For x = 0.1, the c/a ratio of the hydrated phase (1.0191) also exceeds the average of the three monoclinic ratios for the dehydrated phase (1.0041). For x > 0.1, hydrated tetragonal phases consistently exhibit higher c/a ratios than their dehydrated analogues.

These results clearly demonstrate that hydration significantly affects the c/a ratio and, by extension, the octahedral tilt angle. Specifically, hydration increases the tilt angle. To our knowledge, this is the first experimental evidence showing that the incorporation of water molecules into a proton-conducting perovskite structure leads to an increase in the octahedral tilt angle.

3.6 Phase diagrams of fully hydrated and dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8)

Fig. 10 presents the phase diagrams, from RT to 1000 °C, of fully hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) in N₂ atmosphere and dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) in vacuum, as determined by temperature-dependent X-ray diffraction. The observed phase transition sequences are as follows:

Fig. 10 Phase diagrams of (a) hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) under nitrogen and (b) dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (0 ≤ x ≤ 0.8) under vacuum.

BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 in N₂:

(Note: phase transformations are reported here instead of phase transitions, as the water content decreases with increasing temperature).

• x = 0: I2/m → Pm3̄m

• x = 0.1–0.4: I4/mcm → Pm3̄m

• x = 0.5–0.8: no phase transition; remains Pm3̄m

BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 in vacuum:

• x = 0 and 0.1: I2/m → I4/mcm → Pm3̄m

• x = 0.2 and 0.3: I4/mcm → Pm3̄m

• x = 0.4–0.8: no phase transition; remains Pm3̄m

Previous studies reported different phase sequences, such as I2/m → R3̄c → Pm3̄m for x = 0.1 and R3̄c → Pm3̄m for x = 0.4, under dry and wet N₂ conditions using X-ray diffraction.²⁶

In those studies, the R3̄c space group (tilt system a⁻a⁻a⁻) was used for refinement of both hydrated and dehydrated samples, in particular for x = 0.4 at RT. In contrast, I4/mcm (tilt system a⁰a⁰c⁻) is preferred for the hydrated phase in the present study, based on several lines of evidence. I4/mcm was unambiguously identified for x = 0.1, 0.2 and 0.3 by the splitting of h00 reflections together with superlattice peaks. For x = 0.4, the h00 splitting is less well resolved, but the persistence of superlattice reflections strongly suggests that the structure remains I4/mcm (Fig. 2b). In addition, for x = 0.4, neutron-diffraction Rietveld refinements show that the I4/mcm model yields superior agreement factors (R_p = 2.85%, R_wp = 3.75%, R_obs = 3.23%, GOF = 2.05) compared with the R3̄c model (R_p = 3.19%, R_wp = 4.13%, R_obs = 4.15%, GOF = 2.26), supporting the choice of I4/mcm. Finally, Pm3̄m was preferred over R3̄c for the dehydrated x = 0.4 phase at RT. The X-ray diffraction pattern shows no splitting of h00, hh0, or hhh reflections, nor the presence of superlattice peaks, confirming cubic Pm3̄m symmetry (tilt system a⁰a⁰a⁰) at RT (Fig. 7c).

Notably, for compositions with x > 0.1, the phase transition temperatures are consistently lower in the dehydrated series compared to their hydrated counterparts (Fig. 10). In both series, the transition temperatures for I2/m → I4/mcm and I4/mcm → Pm3̄m decrease with increasing Zr content. This compositional trend is consistent with literature reports for BaZr_xCe_0.8−xY_0.2O_3−δ (0 ≤ x ≤ 0.8) in O₂ with 3.1% H₂O,²⁵ where the following phase sequences were observed:

• x = 0.0, 0.1: I2/m → Imma → Pm3̄m

• x = 0.2, 0.3: I2/m → Pm3̄m

• x = 0.4–0.8: Pm3̄m over the entire temperature range

These behaviors can be rationalized using bond valence sum (BVS) analysis applied to both actual and hypothetical cubic structures, highlighting the role of lattice distortions and ionic radii in driving structural transitions.

3.7 BVS as a predictor for octahedral tilting

Bond valence sum (BVS) analysis is a powerful method for evaluating cation stability in irregular coordination environments. It is calculated using the equation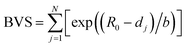 where d_j is the distance to the j-th anion site (d_j is provided in the CIF files available in the supplementary information), R₀ and b are empirically tabulated constants (b = 0.37, R₀ = 2.09 (Ce), 1.937 (Zr), 2.014 (Y), and 1.985 (Yb)),^13,36 and N is the coordination number of the central cation.

Beyond its traditional use in assessing bonding environments, BVS can serve as a predictor of octahedral tilting, similar in concept to the Goldschmidt tolerance factor. However, BVS offers a key advantage: it explicitly accounts for oxygen vacancies, enabling more accurate structural predictions in nonstoichiometric systems.

Importantly, reduced unit cell volumes remain consistent across different space groups (e.g., I2/m, I4/mcm, Pm3̄m), allowing direct comparisons of actual BVS values to those of hypothetical cubic analogues. For this analysis, RT structural data were used:

• Fully hydrated phases: neutron diffraction for x = 0 to 0.4

• Fully hydrated phases in N₂: X-ray diffraction for x = 0.5 to 0.8

• Dehydrated phases in vacuum: X-ray diffraction for x = 0.4, 0.6, and 0.8

BVS values were computed at the B-site (Zr/Ce/Y/Yb), weighted by cation proportions. A coordination of six oxygen atoms was assumed for totally hydrated samples and 5.8 for dehydrated ones, reflecting the presence of oxygen vacancies. For example, for the fully hydrated x = 0 sample obtained from neutron diffraction refinement, the oxidation states for Ce, Y, and Yb are 4.04, 3.29, and 3.04, respectively, giving BVS = 3.86. In the hypothetical case that the structure adopts cubic symmetry while maintaining the same volume as the monoclinic structure, the corresponding oxidation states become 4.47, 3.64, and 3.37, yielding BVS = 4.27.

3.7.1 Interpretation of BVS results. Fig. 11 presents the calculated BVS values. The horizontal dashed line at y = 3.8 represents the ideal valence sum expected from nominal B-site oxidation states. For the hypothetical cubic structures of hydrated phases (x = 0 to 0.4), BVS values (blue crossed squares) are relatively high, ranging from 4.27 (x = 0) to 4.10 (x = 0.4). In contrast, the actual hydrated structures (blue open triangles/diamonds) yield lower BVS values, from 3.86 (x = 0.0) to 3.95 (x = 0.4). These values are closer to the ideal and suggest that lower-symmetry structures are stabilized via octahedral tilting to achieve a more favorable bonding environment.

Fig. 11 Bond valence sum (BVS) calculations at the B-site with respect to the hypothetical cubic structure and the experimentally determined symmetry for dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 and hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (0 ≤ x ≤ 0.8) at RT.

As x increases, the BVS of real hydrated structures gradually rises, while that of the hypothetical cubic counterparts decreases, both converging near x ≈ 0.5. For example, at x = 0.4, the hypothetical cubic structure yields a BVS of 4.10, while the actual tetragonal structure gives 3.96. At x = 0.5, the BVS reaches 4.03, and the phase adopts cubic symmetry, as confirmed by the disappearance of spontaneous tetragonal strain (see Section 3.2.5). For x > 0.5, BVS values decline steadily, reaching 3.81 at x = 0.8, very close to the ideal 3.8, confirming stability of the cubic phase.

For dehydrated phases, although unit cell volumes are lower than those of the corresponding hydrated samples (Tables 2 and 4), oxygen vacancies exert a stronger influence on BVS than volume contraction. As a result, BVS values for dehydrated phases (red crossed squares) are significantly lower than those for the corresponding hydrated samples, ranging from 4.17 (x = 0.0) to 4.02 (x = 0.3). As x increases, BVS approaches the ideal value more rapidly than in the hydrated series. Cubic symmetry is already observed at x = 0.4 in the dehydrated samples, compared with x = 0.5 in the hydrated case. (Note: for x = 0.0–0.3 in the dehydrated phases, the oxygen positions have not been refined; consequently, BVS values are not shown for these compositions). From x = 0.4 to 0.8, BVS continues to decrease, reaching 3.74 at x = 0.8, which is sufficient to stabilize the cubic structure.

Since BVS values generally decrease with increasing temperature, and dehydrated phases exhibit lower BVS values at room temperature compared to their hydrated counterparts, they are more prone to adopting cubic symmetry at lower temperatures. This trend is confirmed for compositions with x = 0.2 and 0.3 (Fig. 10).

This analysis underscores the value of BVS as a predictive tool for understanding symmetry transitions in perovskite-type oxides. By quantifying local bonding environments, including the effects of oxygen vacancies, BVS complements the Goldschmidt tolerance factor, capturing subtle compositional and thermal influences on structural distortions that are otherwise difficult to assess.

4. Conclusions

In this work, we successfully obtained both fully hydrated and fully dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 phases. The fully hydrated state was unambiguously confirmed by TGA and neutron diffraction, while the fully dehydrated state was validated by the near-linear cell-volume behavior during cooling. Using these well-defined phases, we systematically investigated the structural evolution by neutron and X-ray diffraction during heating in N₂ atmosphere and cooling under vacuum. Water uptake was found to strongly affect the crystal structure by increasing octahedral tilting and inducing chemical expansion, which correlated with unit-cell volume changes and TGA-measured water loss. Phase diagrams further revealed that increasing zirconium content reduces symmetry and lowers phase-transition temperatures. While the Goldschmidt tolerance factor alone could not fully capture structural stability, bond-valence-sum (BVS) analysis, which accounts for oxygen vacancies, provided improved predictive capability for octahedral tilting and phase transitions.

Overall, this study establishes the reliable preparation of fully hydrated and dehydrated perovskite phases, clarifies their structure–hydration relationships, and demonstrates the value of BVS analysis as a complementary tool for designing next-generation ceramic proton conductors with enhanced performance.

Author contributions

Lozane Hamze: writing – review & editing, visualization, investigation, formal analysis, data curation. Olivier Joubert: writing – review & editing, funding acquisition. Eric Quarez: writing – original draft, writing – review & editing, validation, supervision, project administration, methodology, conceptualization.

Conflicts of interest

There are no conflicts to declare.

Data availability

Further data relevant to this article are available on request from the corresponding author.

All data supporting the results of this work are available in the main article and in the supplementary information (SI). Supplementary information: crystallographic data at RT for fully hydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9(H₂O)_0.1 (x = 0, 0.1, 0.2, 0.3, and 0.4), without hydrogen localization and derived from neutron diffraction data, as well as for x = 0.5, 0.6, 0.7, and 0.8 obtained from XRD data, and for dehydrated BaZr_xCe_0.8−xY_0.1Yb_0.1O_2.9 (x = 0.4, 0.6, and 0.8) obtained from XRD data, have been deposited via the joint CCDC/FIZ Karlsruhe service under deposition numbers 2471699–2471710.^37a–l The corresponding CIF files, anisotropic thermal displacement parameters, and XRD patterns are available in the SI. See DOI: https://doi.org/10.1039/d5ta07218b.

Acknowledgements

The authors acknowledge support from the French National Research Agency (ANR) under France 2030 program and reference ANR-22-PEHY-0006 (project PEPRH2-PROTEC). The author would like to thank ILL for providing beam time and Dr Emmanuelle Suard for her help with the measurements on the D2B powder diffractometer, Dr Pierre Emmanuel Petit responsible for the diffractometers in the IMN's characterization platform PLASSMAT, Nantes, France.

References

1. L. Yang, S. Wang, K. Blinn, M. Liu, Z. Liu, Z. Cheng and M. Liu, Science, 2009, 326, 126–129.
2. N. A. Danilov, I. A. Starostina, G. N. Starostin, A. V. Kasyanova, D. A. Medvedev and Z. Shao, Adv. Energy Mater., 2023, 13, 2302175.
3. M. B. Hanif, S. Rauf, Z. ul Abadeen, K. Khan, Z. Tayyab, S. Qayyum, M. Mosiałek, Z. Shao, C.-X. Li and M. Motola, Matter, 2023, 6, 1782–1830.
4. S. Guo, L. Jiang, Y. Li, P. Zhong, S. A. Ismail, T. Norby and D. Han, Adv. Funct. Mater., 2024, 34, 2304729.
5. C. Tang, Y. Yao, N. Wang, X. Zhang, F. Zheng, L. Du, D. Luo, Y. Aoki and S. Ye, InfoMat, 2024, 6, e12515.
6. U. Tariq, M. Z. Khan, O. Gohar, Z. U. Din Babar, F. Ali, R. A. Malik, I. A. Starostina, I. A. Samia, J. Rehman, I. Hussain, M. Saleem, A. Ghaffar, M. A. Marwat, K. Zheng, M. Motola and M. B. Hanif, J. Power Sources, 2024, 613, 234910.
7. J. Rehman, M. B. Hanif, M. Z. Khan, M. Ullah, I. A. Starostina, M. T. Muhammad and Z. Li, Energy Fuels, 2024, 38, 22637–22665.
8. H. Nie, Z. Liu, M. Xiao, G. Yang, T. Li, I. A. Starostina, D. A. Medvedev, W. Wang, W. Zhou and R. Ran, Adv. Funct. Mater., 2025, 35, 2416651.
9. J. Wang, W. Chen, Y. Wang, J. Wei, W. Zhang, C. Sun and S. Peng, Mater. Sci. Eng., B, 2025, 317, 118188.
10. L. Hamze, A. Le Gal La Salle, O. Joubert and E. Quarez, Int. J. Hydrogen Energy, 2025, 139, 316–324.
11. S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210.
12. L. Hamze, E. Suard, O. Joubert and E. Quarez, Solid State Ionics, 2024, 417, 116682.
13. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. Cryst. Mater., 2014, 229, 345–352.
14. J. F. Berar and P. Lelann, J. Appl. Crystallogr., 1991, 24, 1–5.
15. E. Quarez, S. Noirault, M. T. Caldes and O. Joubert, J. Power Sources, 2010, 195, 1136–1141.
16. S. Noirault, E. Quarez, Y. Piffard and O. Joubert, Solid State Ionics, 2009, 180, 1157–1163.
17. A. Jarry, E. Quarez, K. Kravchyk and O. Joubert, Solid State Ionics, 2012, 216, 11–14.
18. A. Jarry, E. Quarez and O. Joubert, Solid State Ionics, 2014, 256, 76–82.
19. A. Jarry, O. Joubert, E. Suard, J. M. Zanotti and E. Quarez, Phys. Chem. Chem. Phys., 2016, 18, 15751–15759.
20. C. Hiraiwa, D. Han, A. Kuramitsu, A. Kuwabara, H. Takeuchi, M. Majima and T. Uda, J. Am. Ceram. Soc., 2013, 96, 879–884.
21. A. K. E. Andersson, S. M. Selbach, C. S. Knee and T. Grande, J. Am. Ceram. Soc., 2014, 97, 2654–2661.
22. D. Han, N. Hatada and T. Uda, J. Am. Ceram. Soc., 2016, 99, 3745–3753.
23. G. C. Mather, G. Heras-Juaristi, C. Ritter, R. O. Fuentes, A. L. Chinelatto, D. Pérez-Coll and U. Amador, Chem. Mater., 2016, 28, 4292–4299.
24. G. Hudish, A. Manerbino, W. G. Coors and S. Ricote, J. Am. Ceram. Soc., 2018, 101, 1298–1309.
25. D. Han, X. Liu, T. S. Bjørheim and T. Uda, Adv. Energy Mater., 2021, 11, 2003149.
26. K. Nomura, H. Shimada, Y. Yamaguchi, W. Shin, Y. Okuyama and Y. Mizutani, J. Electrochem. Soc., 2022, 169, 024516.
27. I. Ivanov, D. Tsvetkov, V. Sereda, D. Malyshkin, A. Sereda, P. Zakiryanov, R. Yagovitin and A. Zuev, Chim. Techno Acta, 2024, 11, 202411422.
28. C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B, 1998, 54, 782–789.
29. M. A. Carpenter, A. I. Becerro and F. Seifert, Am. Mineral., 2001, 86, 348–363.
30. T. K.-Y. Wong, B. J. Kennedy, C. J. Howard, B. A. Hunter and T. Vogt, J. Solid State Chem., 2001, 156, 255–263.
31. B. J. Kennedy, C. J. Howard, G. J. Thorogood and J. R. Hester, J. Solid State Chem., 2001, 161, 106–112.
32. I. Qasim, P. E. R. Blanchard, B. J. Kennedy, T. Kamiyama, P. Miao and S. Torii, J. Solid State Chem., 2014, 213, 293–300.
33. V. Jayaraman, A. Magrez, M. Caldes, O. Joubert, F. Taulelle, J. Rodriguez-Carvajal, Y. Piffard and L. Brohan, Solid State Ionics, 2004, 170, 25–32.
34. Y. Zhang, Inorg. Chem., 1982, 21, 3886–3889.
35. Yu. G. Lyagaeva, D. A. Medvedev, A. K. Demin, P. Tsiakaras and O. G. Reznitskikh, Phys. Solid State, 2015, 57, 285–289.
36. N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B, 1991, 47, 192–197.
37. (a) CCDC 2471699: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz07x; (b) CCDC 2471700: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz08y; (c) CCDC 2471701: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz09z; (d) CCDC 2471702: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0b0; (e) CCDC 2471703: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0c1; (f) CCDC 2471704: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0d2; (g) CCDC 2471705: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0f3; (h) CCDC 2471706: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0g4; (i) CCDC 2471707: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0h5; (j) CCDC 2471708: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0j6; (k) CCDC 2471709: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0k7; (l) CCDC 2471710: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2nz0l8.

---