Open Access Article
Open Access ArticleDesign principles of biphenylene-supported dual-atom catalysts for efficient and selective nitrate reduction to ammonia
Kiruthika
Pandiyan
 and
Hsin-Tsung
Chen
and
Hsin-Tsung
Chen
 *
*
Department of Chemistry, Research Center for Semiconductor Materials and Advanced Optics, and R&D Center for Membrane Technology, Chung Yuan Christian University, Chungli District, Taoyuan City 320314, Taiwan. E-mail: htchen@cycu.edu.tw; Tel: +886-3-265-3324
First published on 20th November 2025
Abstract
The electrochemical nitrate reduction reaction (NO3RR) offers a sustainable approach for converting nitrate pollutants into valuable ammonia under ambient conditions. Herein, we employ density functional theory (DFT) to systematically investigate the catalytic potential of homonuclear transition metal dual-atom catalysts (DACs) anchored on biphenylene (TM2@BPN) for NO3RR. Among 28 candidates, five DACs: Mo2@BPN, Ru2@BPN, Rh2@BPN, Os2@BPN, and Ir2@BPN, exhibit low limiting potentials (−0.40 to −0.16 V) and exceptional ammonia selectivity. Rh2@BPN, in particular, achieves a theoretical faradaic efficiency of 100%, effectively suppressing competing hydrogen evolution. Electronic analyses reveal that dual-site π-donation/π*-back-donation interactions, d-band center tuning, and charge redistribution collectively enhance NO3− activation compared to single-atom analogues. Importantly, descriptor-based volcano plots (ΔG*NO3, εd, and ψ) establish generalizable design rules that correlate electronic structure with catalytic trends, enabling predictive DAC screening beyond exhaustive pathway calculations. Ab initio molecular dynamics simulations further confirm the thermal stability of the most active DACs. This work introduces biphenylene as a robust support for stabilizing DACs, establishes structure–property–performance correlations, and provides transferable mechanistic and descriptor-based insights for the rational design of next-generation catalysts for selective multi-electron electrochemical transformations such as nitrate-to-ammonia conversion.
1. Introduction
Nitrate contamination has emerged as a global environmental concern due to the excessive use of fertilizers, industrial emissions, and wastewater discharge. The accumulation of nitrate in aquatic systems not only disrupts ecosystems but also poses severe health risks upon conversion to toxic nitrites in the human body.1–5 Traditional remediation strategies—chemical, physical, or biological—often suffer from high cost, energy intensity, or operational complexity.6,7 In contrast, the electrochemical nitrate reduction reaction (NO3RR) offers a sustainable route to both detoxify nitrate and synthesize ammonia (NH3), a valuable chemical feedstock and potential hydrogen carrier.8–12 While the Haber–Bosch process remains the industrial standard for ammonia synthesis, it is highly energy-intensive and carbon-emissive. Direct electrochemical ammonia production via the nitrogen reduction reaction (NRR) is appealing but limited by the inertness of N2 and its low solubility.13–15 In comparison, NO3RR is more kinetically favorable due to the lower bond dissociation energy of the N–O bond and the higher solubility of nitrate in aqueous media, making it a promising alternative for green ammonia synthesis.16 However, NO3RR is a complex eight-electron, nine-proton transfer process with multiple intermediates and competing side reactions such as hydrogen evolution.17–19 Achieving high activity and selectivity requires the development of advanced catalysts with well-tuned binding energies. Single-atom catalysts (SACs) have drawn significant interest due to their maximal atom utilization and high activity, but their isolated active sites often struggle with multistep reactions due to linear scaling limitations.20–23Dual-atom catalysts (DACs), comprising two adjacent metal atoms, have recently emerged as a promising class of materials that combine the advantages of SACs with synergistic effects. These dual sites enable independent optimization of multiple reaction steps, making DACs particularly attractive for complex processes like NO3RR.24–28 For example, the Cu2 embedded on n-doped graphene was experimentally verified and exhibited good activity for NO3RR with 97.4% faradaic efficiency.29 Fe/Cu diatomic catalysts on nitrogen-doped graphene achieving faradaic efficiencies up to 92.5% at −0.3 V vs. RHE demonstrate strong potential, yet they often rely on heterogeneous dual-atom sites and systematic prediction and design of homonuclear DACs has been less explored.30 Additionally, high-throughput computational screening of M1M2@g-CN DACs (eg FeMo@g-CN, CrMo@g-CN) has identified promising heterogeneous dual-metal combinations, but descriptors correlating electronic structure to performance are still diverse.31 Moreover, reviews of NO3RR underscore that mechanical understanding, especially linking the electronic structure of active dual metal sites, to ammonia selectivity, remains underdeveloped.32 Despite recent progress, rational screening of DACs for NO3RR remains limited, and suitable supports that can stabilize and electronically engage dual-metal centers are critically needed. In particular, the potential of homonuclear DACs for NO3RR remains largely unexplored, how the electronic structure of homonuclear DACs influences the activity and selectivity towards ammonia formation, and reliable electronic descriptors for predicting their catalytic behavior are still lacking.
Herein, we explore biphenylene (BPN)—a recently synthesized sp2-hybridized carbon allotrope featuring four-, six-, and eight-membered rings—as a novel support for homonuclear transition metal DACs. Unlike graphene and other 2D carbon materials the intrinsic ring topology provides a porous lattice with a large number of low-coordination sites that can efficiently stabilize metal atoms. In specific cases, BPN outperforms graphene in catalytic performance due to its higher σ-center position (−7.49 eV vs. −8.09 eV), which allows for greater interaction with reaction intermediates. BPN offers high thermal stability with high thermal conductivity and electrical stability and unique electronic properties including metallic behavior with a tilted Dirac cone above the Fermi level and strong in-plane anisotropy conducive to electrocatalysis.33–37 BPN is a promising catalyst for various reactions, including HER,38 OER,39 CO2RR,40 and NRR.41 In addition, BPN can anchor transition-metal atoms without needing engineered defects or dopant heteroatoms, leading to highly active single-atom Pd@Bip catalysts with very low overpotentials for HER (∼0.05 V) and OER (∼0.50 V), outperforming many conventional catalysts.42 Given the unique advantages of BPN, it is desirable to investigate the potential of BPN for NO3RR and its underlying catalytic mechanism, which has not been reported until now.
Using density functional theory (DFT), we systematically investigate 28 TM2@BPN catalysts for NO3RR, evaluating their activity, selectivity, electronic structure, and thermal stability. After assessing 28 candidates of TM2@BPN, 21 homonuclear DACs that exhibit thermodynamic stability were selected for further investigation. Our screening identifies five promising DACs, Mo2@BPN, Ru2@BPN, Rh2@BPN, Os2@BPN, and Ir2@BPN that exhibit low limiting potentials and excellent selectivity toward NH3. In particular, Rh2@BPN demonstrates a theoretical faradaic efficiency of 100%. Electronic structure analysis, descriptor-based volcano plots, and ab initio molecular dynamics simulations reveal structure–property–performance relationships that provide fundamental insight and design principles for next-generation NO3RR catalysts.
2. Computational details
All spin-polarized density functional theory (DFT) computations were performed using the Vienna ab initio simulation package (VASP).43 The projected augmented wave (PAW)44 approach was used to characterize ion–electron interactions. The generalized gradient approximation in the form of the Perdew–Burke–Ernzerhof (PBE)45 functional was used to treat the exchange correlation energy. The DFT-D3 approach is used to correct van der Waals interactions.46 An energy cutoff of 500 eV was adopted for the plane-wave basis. To prevent interactions between periodic pictures, a 15 Å vacuum space was employed perpendicular to the 2D layer. The convergence criteria for force and total energy during the structural optimization were 0.02 eV Å−1 and 10−5 eV, respectively. For structural optimizations, the Monkhorst-Pack47 approach was used to sample the Brillouin zone with 3 × 3 × 1 k-points, while electronic property computations employed denser k-points of 6 × 6 × 1. Ab initio molecular dynamic (AIMD)48 simulation is used to determine the catalysts' thermal stability, with a temperature of 500 K and a simulation time of 10 ps. The charge transfer was analyzed using the Bader charge technique.49 To examine the electron interaction, the projected crystal orbital Hamiltonian populations (pCOHP)50 were computed. In the NO3RR, the adsorption energies of every potential intermediate are described as,| Eads = Etotal − Esubstrate − Eadsorbate | (1) |
| ΔG = ΔE + ΔEZPE − TΔS + ΔGU + ΔGpH | (2) |
ΔGU is the applied potential with 0 V in this study, and ΔGpH is considered as the correction free energy of H+, which can be calculated using the equation that follows:
| ΔGpH = 2.303 × kBT × pH | (3) |
| UL = −ΔGmax/e | (4) |
| ΔG*NO3 = G*NO3 − G* − GHNO3 (g) + 1/2GH2 (g) + ΔGcorrect | (5) |
3. Results and discussion
3.1 Structure of BPN and stability of TM2@BPN
Fig. 1a shows the optimal structure (3 × 3) of biphenylene, a two-dimensional material containing two chemically different carbon sites, namely C1 and C2. Our optimized BPN lattice parameters were a = 4.52 Å and b = 3.77 Å, consistent with prior computational results.53 BPN is structured with alternating four, six, and eight-membered carbon rings, this arrangement distinguishes it from graphene and other sp2-carbon networks, resulting in distinct electrical and geometric features. Density functional theory studies have revealed that the non-uniform C–C bonds in biphenylene results in anisotropic electronic characteristics. We calculated the electron localization function (ELF) to acquire additional insights into the electrical structure of the BPN.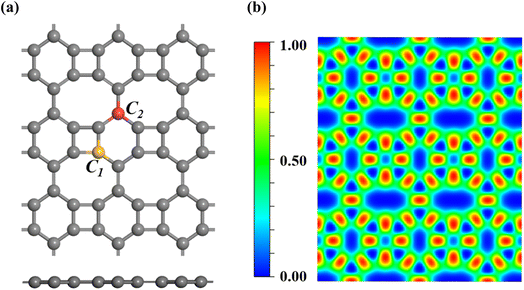 | ||
| Fig. 1 (a) Optimized structure of BPN substrate, with C1 and C2 carbon highlighted. (b) The electron localization function (ELF) of BPN. | ||
As shown in Fig. 1b, the electron localization function of BPN ranges from 0 au (blue) to 1 au (red), where higher values indicate stronger electron localization. The BPN showed discrete regions with values of roughly 0.5 au, indicating delocalized electrical structure. The C–C bond has a maximum value of around 0.9 au, indicating the presence of a strong covalent connection in BPN.
The TM2@BPN system was designed by anchoring 28 TM dimers (TM = 3d, 4d, 5d) to the BPN surface. As shown in Fig. S1, four potential TM dimer anchoring configurations were considered: (I) C1–C1 bridging in a six-membered ring, (II) C1–C1 bridging in an eight-membered ring, (III) top C1 site in an eight-membered ring, and (IV) C2–C2 bridging in an eight-membered ring. The stability and relative energy of these TM dimer anchoring configurations have been thoroughly investigated in previous reports.41Fig. 2a depicts the most stable anchoring configurations after the structural optimization. Using the most energetically favorable configurations, we investigated the stability of TM2@BPN by calculating the binding and cohesive energy. To assess the binding strength between the TM dimer and the BPN substrate, the binding energy (Ebin) was calculated as follows:
| Ebin = ETM2@BPN − EBPN − 2ETM | (6) |
| Ecoh = (Ebulk − nETM)/n | (7) |
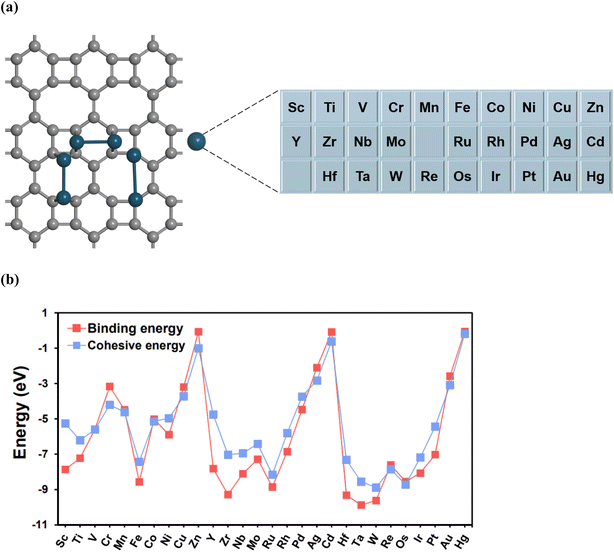 | ||
| Fig. 2 (a) The stable binding configurations of TM2@BPN, with 28 transition metals considered for anchoring on BPN substrate, (b) Binding and cohesive energy comparison plot for TM2@BPN. | ||
3.2 NO3− adsorption
The initial phase of the NO3RR process entails the adsorption of nitrate, a decisive factor that determines the overall catalytic reaction. Dual metal sites provide multiple adsorption possibilities for the NO3− adsorbate. In this study we have considered three different adsorption configurations in order to determine the most stable NO3− adsorption on the catalyst surface. The geometries are based on the number of oxygen atoms bonded to the active sites: monodentate (η1-O-1) when a single oxygen binds to one metal site; chelating bidentate (η2-O-1) when two oxygens bind to the same metal site; and bridging bidentate (η2-O-2) when two oxygens bridge between two metal sites (Fig. S2). As summarized in Table S4, our findings indicate that the NO3− prefers to form a bond with the dual metals by adopting a (η2-O-2) bidentate configuration. The bond length between the metals and oxygen atom is less than 3Å (Table S5), indicating that the bidentate configuration has a strong hold of NO3−. The presence of H+ ions in the reaction promotes competition between NO3RR and HER, resulting in low selectivity and faradaic efficiency of the NO3RR catalyst. In this study, we have investigated two approaches for evaluating the catalyst's selectivity: comparing the adsorption free energy of *NO3− and *H on the catalyst and comparing the limiting potential of HER and NO3RR. First, we will consider the adsorption free energies. Fig. 3a displays the adsorption free energies of NO3− (ΔG*NO3), and H (ΔG*H), for comparison. The results revealed that ΔG*NO3 values are significantly more negative (ranging from −3.20 eV to −0.91 eV) than ΔG*H (ranging from −1.52 eV to 0.43 eV), and this trend is consistent across all TM2@BPN systems. Thus, the active regions of the TM dimers will predominantly adsorb NO3− over H atoms, thereby suppressing the HER. Table S6 summarizes the calculated values of the *H adsorption free energies. The adsorption free energy values of *NO3− indicates that the early transition metals display stronger chemisorption as compared to later transition metals. This behavior can be attributed to early transition metals having fewer d electrons, resulting in greater d-orbital availability and consequently, stronger adsorption; in contrast, late transition metals exhibit a reverse trend. Fig. 3b displays the relationship between the charge transfer of the TM dimer and the adsorption free energy of *NO3− (ΔG*NO3), for better comprehension of the *NO3− adsorption pattern on TM2@BPN (Table S7). There is a linear relationship with a strong correlation coefficient of R2 = 0.84, which confirms that stronger NO3− adsorption is attributed to a substantial charge transfer from the TM dimer to the adsorbate. For illustration, Ti2@BPN has the strongest adsorption strength of −3.20 eV and the maximum charge transfer of 1.13 e−. | ||
| Fig. 3 (a) Comparison of adsorption free energies of NO3−, and H on TM2@BPN. (b) The scaling relationship between NO3− adsorption free energies and charge transfer of TM dimers. | ||
3.3 NO3RR mechanism on TM2@BPN
The process of NO3RR proceeds via the transfer of eight electrons and nine protons.13 The intricacy of the reaction mechanism originates from a complex network of intermediates and byproducts, including NO, NO2, N2O and N2. Additionally, a wide range of intermediate adsorption configurations are possible, resulting in numerous hydrogenation sites for each intermediate. To forecast the most optimal reaction mechanism on TM2@BPN, the stable intermediate from each step is chosen for the subsequent hydrogenation step. Fig. 4 shows the possible NO3RR pathways on TM2@BPN. Nitrate ion adsorption (η2-O-2) serves as the primary step in the reaction mechanism, the most readily accessible O atom is then protonated, and a N–O bond is broken, forming *OH–*NO2. The subsequent hydrogenation leads to the formation of the *NO2 intermediate. After two hydrogenations, the water molecule is released, generating a crucial intermediate, *NO. In TM2@BPN, the *NO adsorption favors both side-on and end-on configurations. Thereby, protonation of *NO leads to the formation of ammonia and an additional water molecule on the substrate. | ||
| Fig. 4 Detailed reaction pathway for NH3 production, as well as NO dimer pathway for N2O, and N2 production. | ||
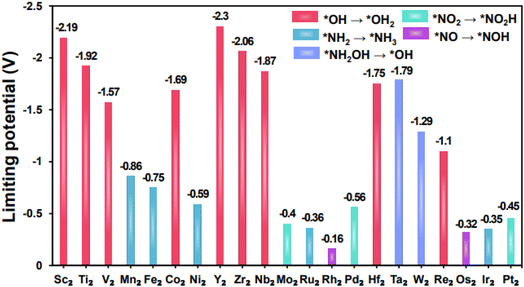
Descriptor based catalyst design serves as a more effective and focused approach for electrocatalytic development and screening.55 The Gibbs free energies of intermediates, which play a critical role in chemical reactions, can function as a primary indicator for predicting the catalytic activity. Therefore, the Gibbs free energy of NO3− is chosen as a descriptor, as nitrate is a key intermediate and its adsorption is an essential step. Fig. 6 shows the graph of limiting potential plotted as a function of the Gibbs free energy of NO3−. Apparently, there is a distinct volcano shaped relationship between them with Rh2@BPN precisely situated at the top of the volcano plot. Apart from, Rh2@BPN additional TM2@BPN systems (highlighted in purple in Fig. 6) are characterized by low limiting potentials (UL). We can deduce that, insufficient adsorption of the catalyst results in a potential determining step (PDS) from *NO to *NOH, while intense adsorption results in high energy demanding step from *NH2 to *NH3/*OH to *OH2. This analysis is consistent with the Sabatier principle, which states that the ideal catalytic activity is achieved if the essential intermediates and catalysts bind with moderate intensity. Accordingly, catalysts with moderate adsorption (ΔG*NO3 between −1.5 to 0.9 eV) have high catalytic activity.
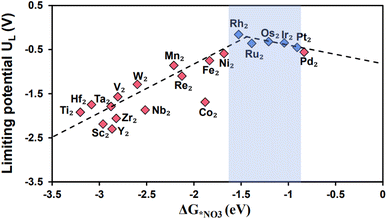 | ||
| Fig. 6 NO3RR Volcano plot of TM2@BPN with the descriptor of Gibbs free energy NO3 (ΔG*NO3) vs. limiting potential (UL). | ||
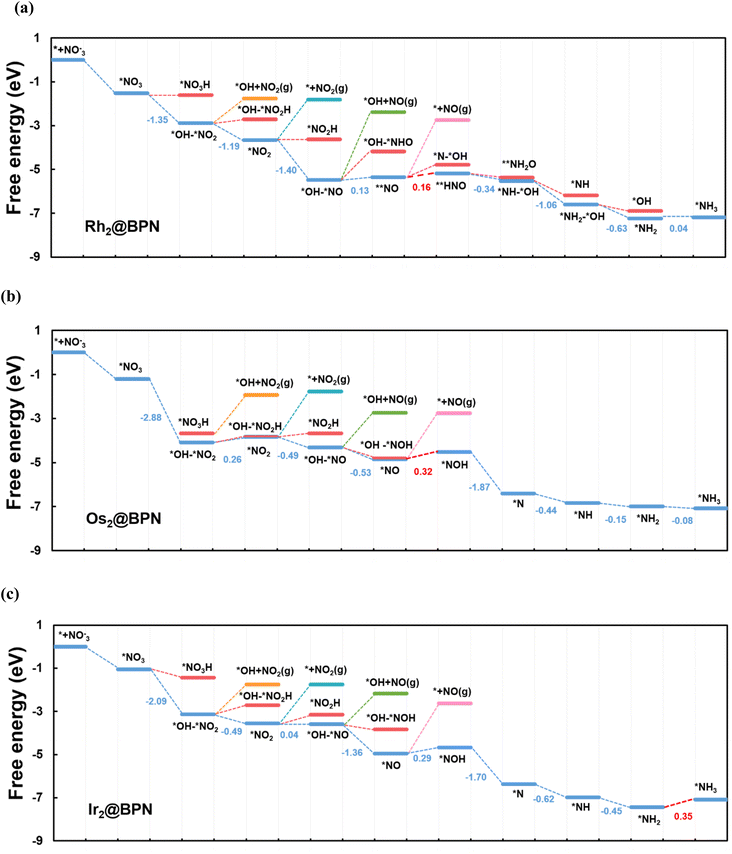
We determined the Gibbs free energy profiles for NO3RR on Rh2@BPN, Os2@BPN, and Ir2@BPN, (Fig. 7a–c) surfaces in order to gain more insight into the reaction mechanism of nitrate reduction to NH3. The DFT-optimized configurations of intermediates associated with the free energy diagram of Rh2@BPN, Os2@BPN and Ir2@BPN are shown in Fig. S3, the computed zero-point energy and entropy are listed in Table S9–S11, and the Gibbs free energy profiles for the remaining DACs are shown in Fig. S4–S9. It is evident that NO3− is strongly chemisorbed on Rh2@BPN, Os2@BPN, and Ir2@BPN via two TM–O bonds, with free energy changes of −1.52, −1.21, −1.04 eV respectively. On Rh2@BPN, the initial proton–electron coupling preferentially attacks the nitrate oxygen interacting with Rh over terminal oxygen. As a result, NO3 dissociates to form *OH–*NO2 with an energy release of −1.35 eV. A similar trend can be identified on Os2@BPN and Ir2@BPN with an exothermic energy change of −2.88 eV, and −2.09 eV respectively. The second hydrogenation step leads to the formation of H2O, which possesses greater energetic stability than the hydrogenation of the *OH–*NO2 molecule to *OH–*NO2H. This step is exothermic by −1.19 eV for Rh2@BPN, and leaves the *NO2 on the active site with two Rh–O bonds. Then *NO2 undergoes hydrogenation in the third step, analogous to that of *NO3− to form *OH–*NO with an energy release of −1.40 eV. The fourth hydrogenation results in the formation of *NO on the Rh–Rh bridging site, following the release of the second water molecule. Three different bonding modes were assessed for *NO adsorption: **NO (binding via the NO-side), *ON (binding via the O-end), and *NO (binding via the N-end) as shown in Fig. S10. Depending on the *NO configuration (NO-end, NO-side, and ON-end), the following hydrogenation will adopt a different pathway. The computed Gibbs free energy for all the binding modes of *NO is tabulated in Table S12. The findings indicate that *NO and **NO modes are thermodynamically more favorable than *ON mode. On Rh2@BPN, *NO is more likely to adsorb via side-on mode (**NO). The hydrogenation of **NO requires an energy input of 0.16 eV to generate **HNO on the active site. Proceeding with the reactions, steps six to eight are enzymatic protonation of the intermediates (*NH–*O → *NH–*OH → *NH2–*OH → *NH2), with corresponding energy changes of −0.34, −1.06, and −0.63 eV respectively, to release the third water molecule and leave *NH2 on the active site. Eventually the *NH2 can be protonated to generate *NH3 with a Gibbs free energy change of 0.04 eV. The potential determining step of NO3RR on Rh2@BPN is the conversion of *NO → *HNO with a low UL of −0.16 eV.
On Os2@BPN, the hydrogenation of *OH–*NO2 results in the formation of NO2 on the active site with two Os–O bonds, this step involves an endothermic contribution of 0.26 eV. Further hydrogenation results in the formation of *NO. On Os2@BPN *NO adsorption prefers the end on mode (*NO) with an energy release of −0.53 eV. The hydrogenation of *NO requires an energy input of 0.32 eV to generate *NOH on the active site. The ensuing hydrogenations are all exothermic and proceed along the *NOH → *N → *NH → *NH2 → *NH3 pathway. The potential determining step of NO3RR on Os2@BPN is the conversion of *NO → *HNO with a UL of −0.32 eV. For Ir2@BPN the adsorption configuration of *NO3 and *NO intermediates and reaction steps throughout the entire protonation pathway are consistent with Os2@BPN. During the entire protonation mechanism on Ir2@BPN, the conversion of NH2 → NH3 requires a maximum energy input of 0.35 eV, identifying it as the potential-determining step. We have performed a climbing-image nudged elastic band (CI-NEB)56,57 calculations for the potential-determining step of the most active catalysts (Rh2@BPN and Os2@BPN). The results obtained from calculations, are as summarized in Fig. S11 and S12. The calculated activation barrier for the PDS was found to be nearly zero, suggesting that the reaction proceeds without a significant kinetic barrier. Therefore, the process is considered kinetically facile, and our discussion primarily focuses on its thermodynamic aspects.
Furthermore, we extensively evaluated the catalytic activity of the related SACs (Rh@BPN, OS@BPN, and Ir@BPN). Our investigation began with identifying the stable binding site for SACs on BPN, and we found that the single metal preferentially binds on the four-membered ring rather than other binding sites, which is consistent with previous findings.58 Subsequently, for nitrate adsorption, we considered two possible configurations, in the (1-O) configuration, one oxygen atom binds to the metal, while in the (2-O) configuration, two oxygen atoms bind to the metal. Among which the (2-O) configuration is the most favorable on SACs, as shown in Fig. S13 and Table S13. Therefore, the 2-O configuration was selected for further reaction pathway analysis. The energy profile diagrams are shown in Fig. S14, the PDS of Rh@BPN, Os@BPN, and Ir@BPN are all *NO → *NOH, with the UL of −1.15, −1.28, and −0.98 V, respectively. It is apparent that the performance of DACs exhibits much better catalytic activity compared to their SACs catalysts and most of the reported electrocatalysts (Table S14).
As discussed earlier, the NO3RR can lead to multiple byproducts, therefore it is important to investigate the reaction pathways in more detail. Consequently, we investigated the Rh2@BPN, Os2@BPN, and Ir2@BPN catalyst's selectivity for possible N-containing byproducts, such as NO2, NO, N2O, and N2. Fig. 7 illustrates that the production of NO2 on Rh2@BPN, Os2@BPN and Ir2@BPN, from *OH–*NO2 is not energetically feasible due to a substantial energy input of 1.11, 2.16 and 1.28 eV respectively, while the hydrogenation of *OH–*NO2 is thermodynamically favorable. Additionally, a large energy input of 2.25, 2.05 and 1.80 eV were required to overcome the barrier for the direct desorption of NO2 from Rh2@BPN, Os2@BPN and Ir2@BPN respectively. Then, the removal of NO from *OH–*NO intermediate demands high energy input of 3.09, 1.58, and 1.43 eV on Rh2@BPN, Os2@BPN and Ir2@BPN respectively. Following this, the hydrogenation of *NO on Rh2@BPN, Os2@BPN and Ir2@BPN is slightly endothermic, with free energy changes of 0.16, 0.32, and 0.29 eV, respectively. Applying a small potential enables further hydrogenation, which is much more favorable thermodynamically than the direct desorption of NO which is high, at 2.60, 2.09, and 2.33 eV, resembling those of NO2. Thus, *NO will be further hydrogenated on Rh2@BPN, Os2@BPN and Ir2@BPN. Conversely, the NO dimer (N2O2), produced via NO–NO coupling, serves as a key precursor for the generation of N2O and N2. After optimization, the NO dimer undergoes bond dissociation, causing N–N bond cleavage. This implies that the NO dimer is unlikely to form, therefore N2O and N2 byproduct formation is also infeasible. In summary, the generation of byproducts (NO2, NO, N2O, and N2) is effectively suppressed, indicating the high NH3 selectivity of Rh2@BPN, Os2@BPN and Ir2@BPN.
3.4 Activity origin of NO3RR on TM2@BPN
The activity trend of NO3RR can be effectively forecasted by the adsorption energy of NO3−, thus understanding its process of activation and variation in adsorption through electronic structure analysis can provide a deeper understanding of the origin of the catalytic behavior. To begin with, the charge density differential (CDD) for TM2@BPN was determined as shown in Fig. S15a and S16. The charge density difference is computed and represented as,| Δρ = ρ(NO3–TM2@BPN) − ρ(TM2@BPN) − ρ(NO3) | (8) |
We will now analyze the origin of TM2@BPN activity from the standpoint of orbital interactions. Fig. S15b provides a schematic representation of the nitrate adsorption mechanism on the TM dimer substrate. In transition metal active sites, the combination of occupied and vacant d orbitals accounts for their strong binding to NO3.The vacant d orbital of TM atoms can accept electrons from the bonding orbital of NO3, strengthening the TM–O adsorption, whereas the occupied d-orbitals of TM atoms contribute electrons back into the empty π* orbital of NO3, thereby weakening the NO bond. Thus, DACs can maximize the activation potential by utilizing the d orbital of the TM dimer site through a “pull–pull” effect, or they can use the intrinsic dual sites to increase the adjustment space.59 Consequently, the TM dimer active site can alter the local electrical environment of the NO3RR active site.
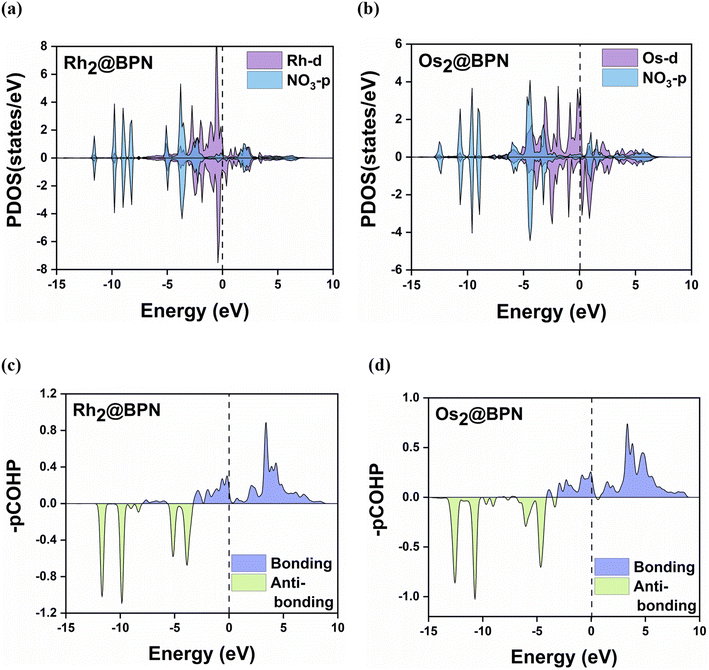
Fig. 8a and b presents the partial density of states (PDOS) for NO3− adsorbed on Rh2@BPN, and Os2@BPN catalysts, while Fig. S17 displays the PDOS for the remaining systems. The PDOS analysis indicates strong π-donation from NO3− to the metal center, as evidenced by the overlap between the occupied NO3−-2p orbitals and the vacant TM-d orbitals below the Fermi level. Furthermore, the small overlap above the Fermi level between the vacant NO3−-2p orbital and the filled TM-d orbitals indicates π*-back-donation. The d–π interaction facilitates mutual electron transfer, strengthening the interaction between NO3− and TM atoms and thereby stabilizing the adsorption complex. The adsorption strength is largely determined by the occupation of antibonding states. The projected crystal orbital Hamilton population (pCOHP) analysis (Fig. 8c and d) indicates that the interaction between the transition metal and nitrate exhibits predominant bonding characteristics, with a strong bonding contribution below the Fermi level. The antibonding states are primarily located above the Fermi level, indicating that they are largely unoccupied, this implies a strong metal–adsorbate interaction.
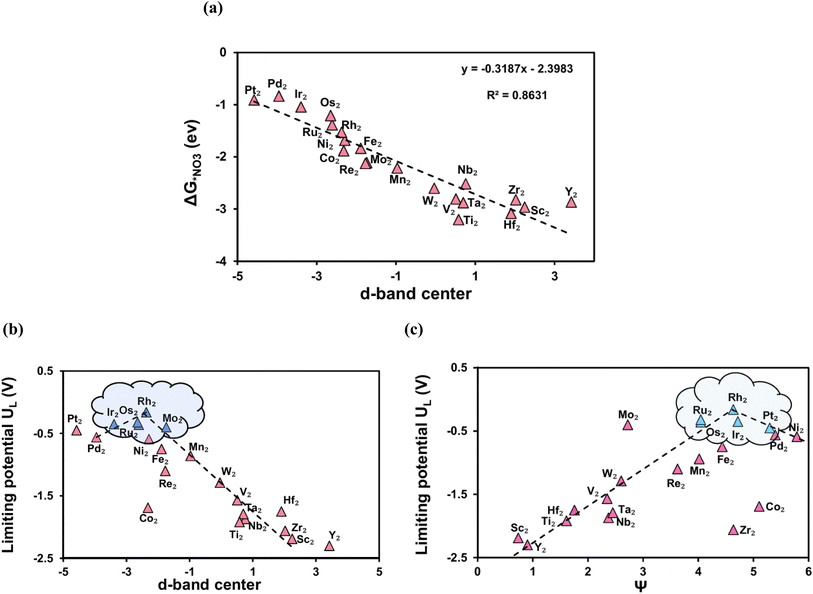
In light of the previous explanation, transition metals' d-orbitals are important for molecular adsorption, and their energy distribution is commonly defined by the d-band center (εd).60 It is widely recognized as an effective descriptor to characterize the interaction strength between small molecules and catalytic sites.55 Therefore, we analyzed the correlation between NO3− free energies and the d-band center to gain insights into NO3− activation (Fig. 9 a). The findings indicate that ΔG*NO3 and εd of the transition metal atoms have a linear connection. When εd approaches the Fermi level, the bonding states are primarily occupied while the antibonding states are largely unoccupied, resulting in greater adsorption. On the other hand, when εd is well below the Fermi level most of the metal's d-orbitals are filled causing the electrons to fill both bonding and antibonding orbitals formed during adsorption, causing weaker adsorption. As a result, Pt with the highest d band center (−4.58 eV), has the lowest adsorption energy (−0.91 eV). Conversely, the metal with the highest adsorption energy Ti (−3.20 eV), has the lowest d-band center (0.57 eV). Rh2@BPN, and Os2@BPN with optimal d-band centers of −2.37 and −2.64 eV respectively, exhibit moderate NO3− adsorption energies, which facilitate efficient NO3RR. Fig. 9b shows a plot of εdvs. UL for TM2@BPN, with Rh2@BPN at the top of the volcano, indicating superior catalytic performance. The volcano plot highlights that the excellent NO3RR performance of DACs results from the optimal positioning of the d-band center. Additionally, we compared the d band center of SACs and DACs in order to examine the mechanism of the synergistic effect between the TM dimer site; the results are provided in Table S15. In the case of Rh@BPN, the d-band center is located at −3.26 eV, which resulted in weak nitrate adsorption (−0.96 eV). However, introducing a second Rh atom (Rh2@BPN) shifts the d-band center closer to the Fermi level, which enhances the adsorption strength. This d-band shift significantly affects the adsorption energies of the reaction intermediates, thereby altering the energy barrier of the potential determining step.
As we have discussed earlier, the d-band is crucial for controlling catalytic activity since its occupancy affects the strength of intermediate adsorption, which in turn regulates the overall efficacy of the reaction. The quantity of d-orbital electrons (Nd), influence the adsorption strength, more d-electrons lower the d-band center, there by weakening the adsorbate binding, whereas less d-electrons enhance it, strengthening adsorption. However, Nd alone cannot explain the activity trend, this effect is further modulated by electronegativity (ETM), which controls charge transfer between the transition metal and its adjacent atoms (C, N, O, or H), thereby regulating the binding of chemical intermediates. To describe the relationships between these two parameters (Nd and ETM), a descriptor ψ was introduced.61,62 Which is represented as,
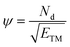 | (9) |
Higher ψ generally means weaker binding to intermediates due to more filled d-orbitals leading to stronger antibonding state occupation. Fig. 9c shows a plot of ψ against UL for TM2@BPN, with Rh2@BPN at the peak of the volcano plot which corresponds to the activity results. This suggests that ψ shows a strong linear correlation with adsorption energies and catalytic activity, providing a predictive tool for designing catalysts TM2@BPN screening of NO3RR catalysts. Using a catalyst's easily available intrinsic nature as a descriptor to forecasting its catalytic activity provides a cost-effective and practical technique, that avoids the need for costly DFT calculations and experimental experiments.
To enable a deeper understanding of reaction pathways and electron transfer mechanisms, the gradual change of charge throughout the reaction pathway of TM2@BPN for NO3RR was investigated based on Bader charge analysis. Each intermediate is subdivided into three moieties (Fig. 10a), moiety 1 corresponds to (BPN support), moiety 2 is the (TM2C4) catalytic site and moiety 3 denotes the adsorbed intermediates involved in the reaction pathway. Fig. 10b, c and S18 display the charge variation on Rh2@BPN, Os2@BPN and Ir2@BPN. Throughout the NO3RR process, all three moieties exhibit variation in charge. During the first step, the NO3− molecule receives 0.74 e−, 0.80 e−, and 0.69 e− from moiety 2 and moiety 1 on Rh2@BPN, Os2@BPN, and Ir2@BPN respectively. The moiety 2 consistently donates electrons to the intermediates, which is important for improving the adsorption of intermediates. The final increase in moiety 3's charge signifies NH3 desorption proceeds without difficulty. Thus, Rh2@BPN, Os2@BPN, and Ir2@BPN exhibit a comparable charge variation trend. As the adsorbed intermediates receive electrons, moiety 1 facilitates electron transfer between the catalytic site and the adsorbed intermediates, allowing the catalytic process to proceed continuously, moiety 2 functions as both the DAC's active site and an electron donor.
 | ||
| Fig. 10 (a) Three moieties of TM2@BPN. (b and c) Charge variation during the process of NO3RR on Rh2@BPN and Os2@BPN. | ||
3.5 Selectivity based on limiting potential and faradaic efficiency
Another factor that hinders NO3RR performance is faradaic efficiency (FE), which is strongly related to competitive HER. To assess the catalytic preference of the active sites, we previously compared the ΔG*NO3− and ΔG*H values. The findings revealed that *NO3 atoms are more likely to occupy the active sites than *H atoms. However, in the electrocatalytic process, UL is the deciding element for the entire reaction. Thus, we analyze the UL for NO3RR and HER to evaluate the catalytic selectivity. Accordingly, the UL of HER should be more negative than the UL of NO3RR. Fig. 11 illustrates the UL of NO3RR and HER, the NO3RR selective is indicated by the area below the diagonal line, while the HER selective is indicated by the area above the diagonal line. Most catalysts effectively inhibit HER, with the exception of Pt. To further support this, the faradaic efficiency of NO3RR was determined using the following formula: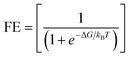 | (10) |
3.6 Thermal stability of TM2@BPN
Additionally, Rh2@BPN, Os2@BPN, and Ir2@BPN were subjected to ab initio molecular dynamics (AIMD) simulations at 500 K for a total duration of 10 ps with a time step of 2 fs to evaluate their thermodynamic stability, as illustrated in Fig. 12 and S19. According to AIMD simulations, the structures of Rh2@BPN, Os2@BPN, and Ir2@BPN remain stable throughout the process, without any dissociation. Furthermore, there were only slight energy variations within a narrow range. This indicates that all three materials remain stable throughout the process and are capable of withstanding high temperatures without notable structural changes.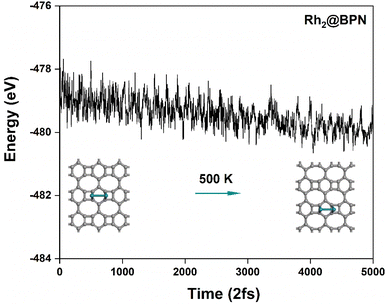 | ||
| Fig. 12 Ab initio molecular dynamics simulation of Rh2@BPN at 500 K for a total duration of 10 ps with a time step of 2 fs. | ||
3.7 Potential experimental synthesis
According to Fan et al. biphenylene (BPN) was recently synthesized by surface-assisted Ullmann coupling of 1,8-dibromobiphenylene precursors on Au (111).35 This indicates that obtaining extended BPN sheets is experimentally feasible. A feasible technique to synthesizing double-metal anchored BPN can be developed by adapting known DAC synthesis strategies and using BPN's distinctive lattice structure. BPN is an excellent substrate for maintaining isolated dual-metal atoms because of its intrinsic periodic pores and defect-rich sites, which offer a large number of anchoring centers with a significant electron-donating capacity.36,63 Reported approaches for DACs include high-temperature pyrolysis of metal–organic frameworks (MOFs) or zeolitic imidazolate frameworks (ZIFs), wet chemical impregnation, electrochemical deposition, and atomic layer deposition.64,65 Using a bottom-up strategy, BPN could be impregnated with bimetallic precursors, including metal–organic complexes of Fe, Co, or Ni, and then pyrolyzed at high temperatures in an inert atmosphere to create atomically distributed dimers that are stabilized by the carbon framework. Alternatively, a sequential anchoring technique utilizing atomic layer deposition can accurately deposit two different metals onto the reactive sites of BPN, ensuring well-defined dual-atom configurations, as proven by Pt2 dimers on carbon supports.66 These methods can facilitate the controlled synthesis of double-metal anchored BPN by taking advantage of its inherent electron-rich bonding environment and high structural stability, offering a solid foundation for investigating synergistic effects in electrocatalysis.4. Conclusion
In summary, density functional theory screening of 28 homonuclear dual-atom catalysts anchored on biphenylene (TM2@BPN) establishes biphenylene as a functionally advantaged support for multistep electrocatalysis. Distinct from graphene-type lattices, BPN presents topologically diverse four-/six-/eight-membered rings and electronically anisotropic sp2 networks, offering abundant, stabilizing anchoring motifs that promote robust dual-site fixation, favorable charge donation, and moderated adsorption energetics along the NO3RR pathway. Guided by these support-induced effects, five DACs: Mo2@BPN, Ru2@BPN, Rh2@BPN, Os2@BPN, and Ir2@BPN deliver low limiting potentials (−0.40 to −0.16 V) and strong ammonia selectivity, with Rh2@BPN achieving a theoretical faradaic efficiency of 100% while suppressing HER and N-oxide byproducts. Mechanistically, the dual-site π-donation/π-back-donation* and d-band center tuning rationalize the activity/selectivity gains over SAC analogues. Beyond identifying high-performance catalysts, this work advances generalizable design rules: (i) target moderate NO3− adsorption (ΔG*NO3 within the volcano apex window) to avoid either early-step or late-step bottlenecks; (ii) engineer d-band centers near optimal alignment to maximize bonding while limiting antibonding population; and (iii) utilize intrinsic electronic descriptors (ΔG*NO3, εd, and ψ) to pre-screen dual-site compositions without exhaustive pathway calculations. These principles, corroborated by AIMD-verified thermal stability on BPN, are transferable to other multi-electron electrochemical conversions that require cooperative active sites. Collectively, our findings position biphenylene-supported DACs as a rational platform for selective nitrate-to-ammonia electroreduction and, more broadly, establish structure–property–performance correlations and descriptor-based principles that can guide the rational design of next-generation catalysts for multi-electron electrochemical transformations.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting the findings of this study are available within the article and its supplementary information (SI). Additional raw data are available from the corresponding author upon reasonable request.Supplementary information: Notes 1, 2 and 3 for elementary and kinetic steps of NO3RR, solvent effect, and faradaic efficiency, four possible binding configurations of TM dimer on BPN (Fig. S1), three possible adsorption configurations of NO3− on TM2@BPN (Fig. S2), DFT-optimized configurations of intermediates associated with free energy diagram of Rh2@BPN, Os2@BPN and Ir2@BPN respectively (Fig. S3), free energy diagram for NO3RR on Mo2@BPN, Ru2@BPN and Pt2@BPN catalysts respectively, (UL > −0.5 V) (Fig. S4), free energy diagram for NO3RR on Sc2@BPN, Ti2@BPN and V2@BPN catalysts respectively (Fig. S5), free energy diagram for NO3RR on Mn2@BPN, Fe2@BPN and Co2@BPN catalysts respectively (Fig. S6), free energy diagram for NO3RR on Ni2@BPN, Y2@BPN and Zr2@BPN catalysts respectively (Fig. S7), free energy diagram for NO3RR on Nb2@BPN, Pd2@BPN and Hf2@BPN catalysts respectively (Fig. S8), free energy diagram for NO3RR on Ta2@BPN, W2@BPN and Re2@BPN catalysts respectively (Fig. S9), three possible adsorption configurations of NO on TM2@BPN (Fig. S10), nudged elastic band calculation results for *NO + (H3O+ + e−) → *NOH + H2O on Rh2@BPN (Fig. S11), nudged elastic band calculation results for *NO + (H3O+ + e−) → *NOH + H2O (Fig. S12), two possible adsorption configurations of NO3− on TM@BPN (Fig. S13), free energy diagram for NO3RR on Rh@BPN, Os@BPN and Ir@BPN SACs catalysts respectively (Fig. S14), (a) charge density differences of nitrate adsorbed on Rh2@BPN, and Os2@BPN the isosurface value is 0.001 e/Å3. (b) Schematic representation of the nitrate adsorption mechanism on the TM dimer (Fig. S15), charge density differences of nitrate adsorbed on Mo2@BPN, Ru2@BPN, Ir2@BPN and Pt2@BPN, the isosurface value is 0.001 e/Å3. The charge depletion and accumulation were depicted by cyan and violet respectively (Fig. S16), partial density of states (PDOS) on the molecular orbital of NO3 and the d orbital of metal atoms on Mo2@BPN, Ru2@BPN, Ir2@BPN and Pt2@BPN catalysts after NO3 adsorption (Fig. S17), three moieties of TM2@BPN and charge variation during the process of NO3RR on Ir2@BPN (Fig. S18), ab initio molecular dynamics simulation of (a) Os2@BPN, and (b) Ir2@BPN was carried out at 500 K for 1 ps over a total time step of fs (Fig. S19). Zero-point energy (ΔEZPE) and entropy (TΔS) at room temperature of gaseous molecules from the NIST database (Table S1), the computed binding energy (Eb), cohesive energy (Ecoh) and the difference between binding and cohesive (Eb–Ecoh) of TM dimers in TM2@BPN (Table S2), electronic and structural properties of TM2@BPN, including transition metal (TM) dimer bond length (dM–M), charge transfer (CT) from TM dimer to substrate, and d band center (εd) (Table S3), calculated adsorption free energy ΔG*NO3 (eV) on TM2@BPN, via (η1-O-1), (η2-O-1) and (η2-O-2) configuration (Table S4), transition metal to oxygen bond distance for the stable NO3− adsorbed configuration (η2-O-2) on TM2@BPN (Table S5), calculated Gibbs free energy of *H (ΔG*H) adsorption on TM2@BPN (Table S6), calculated charge transfer (CT) from TM dimer to NO3−, on TM2@BPN (Table S7), the Computed limiting potential (UL) and potential determining step (PDS) of TM2@BPN for NO3RR (Table S8), the calculated Zero-point energy (ΔEZPE) and entropic contributions (TΔS) at room temperature (298.15 K) to the Gibbs free energies of each elementary step for Rh2@BPN. The unit is eV (Table S9), the calculated Zero-point energy (ΔEZPE) and entropic contributions (TΔS) at room temperature (298.15 K) to the Gibbs free energies of each elementary step for Os2@BPN. The unit is eV (Table S10), the calculated Zero-point energy (ΔEZPE) and entropic contributions (TΔS) at room temperature (298.15 K) to the Gibbs free energies of each elementary step for Ir2@BPN. The unit is eV (Table S11),calculated adsorption free energy ΔG*NO (eV) on TM2@BPN, via *NO end, *ON end, and **NO side configurations (Table S12), calculated adsorption free energy ΔG*NO3 (eV) on TM@BPN, via 1-O, and 2-O configuration (Table S13), the comparison of catalytic performance (reflected by limiting potential, UL) for Nitrate reduction reaction on various electrocatalysts (Table S14), calculated d-band center (εd) of TM@BPN (Table S15), calculated limiting potential of HER and NO3RR and faradaic efficiency (FE) values for TM2@BPN (Table S16), comparison of nitrate reduction reaction pathways on the Rh2@BPN by using DFT-D3 and DFT-Sol method (Table S17), comparison of nitrate reduction reaction pathways on the Os2@BPN by using DFT-D3 and DFT-Sol method (Table S18). See DOI: https://doi.org/10.1039/d5ta07089a.
Acknowledgements
H.-T. Chen gratefully thanks the Chung Yuan Christian University (CYCU), National Center for Theoretical Sciences (NCTS), and National Science and Technology Council (NSTC), Taiwan, under Grant Numbers, NSTC 114-2113-M-033-002, 114-2113-M-007-026, 113-2113-M-033-007, and 113-2113-M-007-027 for the financial support and the National Center for High-performance Computing (NCHC), Taiwan, for providing computational and storage resources.References
- D. E. Canfield, A. N. Glazer and P. G. Falkowski, Science, 2010, 330, 192–196 CrossRef CAS.
- K. R. Burow, B. T. Nolan, M. G. Rupert and N. M. Dubrovsky, Environ. Sci. Technol., 2010, 44, 4988–4997 CrossRef CAS PubMed.
- N. Gruber and J. N. Galloway, Nature, 2008, 451, 293–296 CrossRef CAS PubMed.
- H. Niu, Z. Zhang, X. Wang, X. Wan, C. Shao and Y. Guo, Adv. Funct. Mater., 2021, 31, 2008533 CrossRef CAS.
- Q. Zhang, B. Liu, L. Yu, Y. Bei and B. Tang, ChemCatChem, 2020, 12, 334–341 CrossRef CAS.
- Y. Wang, Y. Yu, R. Jia, C. Zhang and B. Zhang, Natl. Sci. Rev., 2019, 6, 730–738 CrossRef CAS.
- Y. Wang, A. Xu, Z. Wang, L. Huang, J. Li, F. Li, J. Wicks, M. Luo, D.-H. Nam, C.-S. Tan, Y. Ding, J. Wu, Y. Lum, C.-T. Dinh, D. Sinton, G. Zheng and E. H. Sargent, J. Am. Chem. Soc., 2020, 142, 5702–5708 CrossRef CAS PubMed.
- J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. M. Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360, eaar6611 CrossRef PubMed.
- H. Jiang, G.-F. Chen, O. Savateev, J. Xue, L.-X. Ding, Z. Liang, M. Antonietti and H. Wang, Angew. Chem., Int. Ed., 2023, 62, e202218717 CrossRef CAS PubMed.
- W. He, J. Zhang, S. Dieckhöfer, S. Varhade, A. C. Brix, A. Lielpetere, S. Seisel, J. R. C. Junqueira and W. Schuhmann, Nat. Commun., 2022, 13, 1129 CrossRef CAS.
- V. Rosca, M. Duca, M. T. de Groot and M. T. M. Koper, Chem. Rev., 2009, 109, 2209–2244 CrossRef CAS PubMed.
- X. Fu, X. Zhao, X. Hu, K. He, Y. Yu, T. Li, Q. Tu, X. Qian, Q. Yue, M. R. Wasielewski and Y. Kang, Appl. Mater. Today, 2020, 19, 100620 CrossRef.
- S. Chen, S. Perathoner, C. Ampelli, C. Mebrahtu, D. Su and G. Centi, Angew. Chem., Int. Ed., 2017, 56, 2699–2703 CrossRef CAS.
- J. M. Walls, J. S. Sagu and K. G. Upul Wijayantha, RSC Adv., 2019, 9, 6387–6394 RSC.
- M. Duca, M. C. Figueiredo, V. Climent, P. Rodriguez, J. M. Feliu and M. T. M. Koper, J. Am. Chem. Soc., 2011, 133, 10928–10939 CrossRef CAS.
- J.-X. Liu, D. Richards, N. Singh and B. R. Goldsmith, ACS Catal., 2019, 9, 7052–7064 CrossRef CAS.
- J. Long, S. Chen, Y. Zhang, C. Guo, X. Fu, D. Deng and J. Xiao, Angew. Chem., Int. Ed., 2020, 59, 9711–9718 CrossRef CAS PubMed.
- F. Dong, M. Wu, Z. Chen, X. Liu, G. Zhang, J. Qiao and S. Sun, Nano-Micro Lett., 2021, 14, 36 CrossRef.
- Y. Wang, J. Mao, X. Meng, L. Yu, D. Deng and X. Bao, Chem. Rev., 2019, 119, 1806–1854 CrossRef CAS PubMed.
- B. Singh, V. Sharma, R. P. Gaikwad, P. Fornasiero, R. Zbořil and M. B. Gawande, Small, 2021, 17, 2006473 CrossRef CAS PubMed.
- H. Fei, J. Dong, Y. Feng, C. S. Allen, C. Wan, B. Volosskiy, M. Li, Z. Zhao, Y. Wang, H. Sun, P. An, W. Chen, Z. Guo, C. Lee, D. Chen, I. Shakir, M. Liu, T. Hu, Y. Li, A. I. Kirkland, X. Duan and Y. Huang, Nat. Catal., 2018, 1, 63–72 CrossRef CAS.
- Y. Wang, Y. Liu, W. Liu, J. Wu, Q. Li, Q. Feng, Z. Chen, X. Xiong, D. Wang and Y. Lei, Energy Environ. Sci., 2020, 13, 4609–4624 RSC.
- D. K. D. Chittibabu, N. Sathishkumar, S.-Y. Wu and H.-T. Chen, ACS Appl. Energy Mater., 2023, 6, 6636–6645 CrossRef CAS.
- T. He, A. R. P. Santiago, Y. Kong, M. A. Ahsan, R. Luque, A. Du and H. Pan, Small, 2022, 18, 2106091 CrossRef CAS.
- S. Zhang, W. Zhang, J. Qian, S.-z. Huang, Q. Chen, E.-y. Ming, Q. Sun and Z. Tong, Research Progress of Magnesium and Its Alloy in Petroleum Field, in Proceedings of the International Field Exploration and Development Conference 2022, IFEDC 2022, ed. J. Lin, Springer Series in Geomechanics and Geoengineering, Springer, Singapore, 2023, pp. 3634–3644 Search PubMed.
- Y. Wang, H. Yin, F. Dong, X. Zhao, Y. Qu, L. Wang, Y. Peng, D. Wang, W. Fang and J. Li, Small, 2023, 19, 2207695 CrossRef CAS PubMed.
- P. Lv, D. Wu, B. He, X. Li, R. Zhu, G. Tang, Z. Lu, D. Ma and Y. Jia, J. Mater. Chem. A, 2022, 10, 9707–9716 RSC.
- F. Rehman, S. Kwon, C. B. Musgrave, M. Tamtaji, W. A. Goddard and Z. Luo, Nano Energy, 2022, 103, 107866 CrossRef CAS.
- T. Zhao, K. Chen, X. Xu, X. Li, X. Zhao, Q. Cai, K. Chu and J. Zhao, Appl. Catal., B, 2023, 339, 123156 CrossRef CAS.
- S. Zhang, J. Wu, M. Zheng, X. Jin, Z. Shen, Z. Li, Y. Wang, Q. Wang, X. Wang, H. Wei, J. Zhang, P. Wang, S. Zhang, L. Yu, L. Dong, Q. Zhu, H. Zhang and J. Lu, Nat. Commun., 2023, 14, 3634 CrossRef CAS.
- Z. Shu, H. Chen, X. Liu, H. Jia, H. Yan and Y. Cai, Adv. Funct. Mater., 2023, 33, 2301493 CrossRef CAS.
- M. M. Islam, S. M. Abu Nayem, S. S. Shah, M. Z. Islam, M. A. Aziz and A. J. Saleh Ahammad, Chem. Rec., 2025, 25, e202400206 CrossRef CAS PubMed.
- B. Mohanty, B. K. Jena and S. Basu, ACS Omega, 2020, 5, 1287–1295 CrossRef CAS.
- J. Cho, A. Medina, I. Saih, J. Il Choi, M. Drexler, W. A. Goddard Iii, F. M. Alamgir and S. S. Jang, Angew. Chem., Int. Ed., 2024, 63, e202320268 CrossRef CAS.
- Q. Fan, L. Yan, M. W. Tripp, O. Krejčí, S. Dimosthenous, S. R. Kachel, M. Chen, A. S. Foster, U. Koert, P. Liljeroth and J. M. Gottfried, Science, 2021, 372, 852–856 CrossRef CAS.
- T. Han, Y. Liu, X. Lv and F. Li, Phys. Chem. Chem. Phys., 2022, 24, 10712–10716 RSC.
- Y. Luo, C. Ren, Y. Xu, J. Yu, S. Wang and M. Sun, Sci. Rep., 2021, 11, 19008 CrossRef CAS.
- J. Hao, Z. Zhao, C. Chen, C. Zhang, L. Li, S. Gao, B. Jia and P. Lu, Sustainable Energy Fuels, 2022, 6, 3446–3452 RSC.
- T. Liu, Y. Jing and Y. Li, J. Phys. Chem. Lett., 2021, 12, 12230–12234 CrossRef CAS.
- N. Xing, Z. Liu, Z. Wang, Y. Gao, Q. Li and H. Wang, Phys. Chem. Chem. Phys., 2022, 24, 27474–27482 RSC.
- K. Pandiyan, D. K. Dhanthala Chittibabu and H.-T. Chen, ACS Appl. Energy Mater., 2024, 7, 10758–10769 CrossRef CAS.
- T.-T. Wang, Y. Meng, H.-C. Huang, L. Zhang and S.-B. Cheng, Phys. Chem. Chem. Phys., 2025, 27, 291–300 RSC.
- G. Sun, J. Kürti, P. Rajczy, M. Kertesz, J. Hafner and G. Kresse, J. Mol. Struct.:THEOCHEM, 2003, 624, 37–45 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J.-C. Chen, H. Cao, J.-W. Chen, S.-J. Qian, G.-J. Xia, Y.-G. Wang and J. Li, J. Phys. Chem. C, 2021, 125, 19821–19830 CrossRef CAS.
- Z. Wang, Z. Yin, Y. Gao, H. Wang, J. Gao and J. Zhao, J. Mater. Chem. A, 2024, 12, 2748–2759 RSC.
- G. Zhang, X. Li, K. Chen, Y. Guo, D. Ma and K. Chu, Angew. Chem., Int. Ed., 2023, 62, e202300054 CrossRef CAS.
- S. Jiao, X. Fu and H. Huang, Adv. Funct. Mater., 2022, 32, 2107651 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2663–2668 CrossRef CAS.
- D. K. D. Chittibabu and H.-T. Chen, Electrochim. Acta, 2024, 497, 144578 CrossRef CAS.
- L. Yang, S. Feng and W. Zhu, J. Hazard. Mater., 2023, 441, 129972 CrossRef CAS.
- L. Yang and W. Zhu, Diamond Relat. Mater., 2022, 128, 109249 CrossRef CAS.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS.
- H. Niu, X. Wang, C. Shao, Z. Zhang and Y. Guo, ACS Sustain. Chem. Eng., 2020, 8, 13749–13758 CrossRef CAS.
- V. Kumar, S. Pratap and B. Chakraborty, J. Phys.: Condens. Matter, 2025, 37, 113006 CrossRef CAS PubMed.
- D. Wu, B. He, Y. Wang, P. Lv, D. Ma and Y. Jia, J. Phys. D: Appl. Phys., 2022, 55, 203001 CrossRef CAS.
- K. Liu, J. Li, Y. Liu, M. Wang and H. Cui, J. Energy Chem., 2023, 79, 515–534 CrossRef CAS.
- H. Yan, Y. Lin, H. Wu, W. Zhang, Z. Sun, H. Cheng, W. Liu, C. Wang, J. Li, X. Huang, T. Yao, J. Yang, S. Wei and J. Lu, Nat. Commun., 2017, 8, 1070 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2026 |