Multiscale structural regulation enables ultra-rapid and stable high-temperature sensing in fergusonite ceramics
Hao
Sun
ab,
Ruifeng
Wu
a,
Yafei
Liu
a,
Jia
Chen
ab,
Jianan
Xu
ab,
Xia
Huang
a,
Aimin
Chang
a and
Bo
Zhang
 *a
*a
aKey Laboratory of Functional Materials and Devices for Special Environmental Conditions (Chinese Academy of Sciences), Xinjiang Key Laboratory of Electronic Information Materials and Devices, Xinjiang Technical Institute of Physics & Chemistry of CAS, Urumqi 830011, China. E-mail: zhangbocas@ms.xjb.ac.cn
bCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
First published on 20th November 2025
Abstract
Precise temperature sensing in extreme high-temperature environments, such as those encountered in energy and aerospace applications, demands high-performance thermosensitive materials, among which fergusonite-type oxide ceramics are prominent candidates. However, due to the complicated local structural design, simultaneously achieving rapid response/recovery, high sensitivity and accuracy under high-temperature conditions remains a challenge. Herein, second-phase precipitation (cubic CeO2) and B-site modulation were introduced in CaCe2Nb2−xTaxMoO12 ceramics by regulating solid solubility and sintering protocols. Synergistic optimization of grain boundaries and defect structure enabled carrier migration channels and precise thermal activation control. Exceptional temperature sensitivity and measurement accuracy were achieved over a broad temperature range (153–773 K), with a rapid response time of 1.82 s and recovery time of 0.76 s at 773 K. Notably, these ceramics demonstrate remarkable stability during thermal cycling and prolonged high-temperature operation. This work presents new material candidates and multiscale regulation strategies for developing high-temperature thermosensitive materials surpassing conventional ceramic systems.
1. Introduction
The reliable operation of equipment across broad temperature ranges in various advanced industrial scenarios is highly dependent on temperature sensors possessing rapid response characteristics and exceptional stability.1–4 In particular, high-temperature thermosensitive materials exhibit significant application potential in critical areas such as in situ temperature monitoring within fuel cell stacks,5 dynamic temperature regulation in new energy vehicle thermal management systems,6 and high-precision temperature compensation for industrial automation,7 owing to their superior thermal stability, precise resistance-temperature characteristics, and favorable structural adaptability across a wide temperature range. Currently, research on high-temperature thermosensitive ceramics is predominantly concentrated on traditional perovskite structures, such as CaTiO3,8 YCr0.5Mn0.5O3,9 and CaCu3Ti4O12.10 Unfortunately, these materials are often confronted with issues including diminished response sensitivity, inadequate long-term stability, and significant resistance drift, which result in a failure to meet the performance requirements under extreme conditions. As an emerging class of high-temperature thermosensitive ceramics, rare-earth niobate (RENbO4) compounds possessing the fergusonite structure exhibit outstanding high-temperature thermal-electric response behavior and structural stability, attributable to their unique charge transport mechanism within the NbOx network11,12 and the lattice contraction effect induced by lanthanide ions.13,14 Therefore, the development and investigation of RENbO4 high-temperature thermosensitive ceramics are essential to satisfy the pressing demand for high-performance, high-stability temperature sensors in advanced industrial settings.Rare-earth RENbO4 materials with the fergusonite structure crystallize in the monoclinic system with space group C2/c.15 Within this structure, rare-earth ions (RE3+) occupy eight-coordinated distorted polyhedral sites, while niobium ions (Nb5+) reside within six-coordinated distorted NbO6 octahedra. Oxygen atoms, connecting through shared vertices or edges, form a three-dimensional framework network.16 Prior research on the high-temperature thermosensitive behavior of RENbO4 has focused predominantly on high-entropy design strategies—specifically, multi-component doping at either the A- or B-sites—to introduce lattice distortion and modulate defect states, thereby optimizing thermosensitive response. For instance, the (Ca0.5Ce0.5)(Nb0.25Ta0.25Mo0.25W0.25)O4 ceramic exhibits favorable linear resistance-temperature behavior across a broad temperature range of 423–1473 K.17 The (La0.2Ce0.2Nd0.2Sm0.2Eu0.2)NbO4 ceramic demonstrates high linearity (R2 = 0.99956) and a remarkably low aging drift rate of merely 0.42% following 1000 hours of aging at 1173 K.18 Furthermore, the (La0.2Ce0.2Pr0.2Gd0.2Y0.2)1−xSrxNbO4−δ material maintains an aging drift rate below 1% even after 1000 hours of high-temperature sensitization and aging treatment, achieving a temperature coefficient of resistance (TCR) of 0.223% K−1 at 1423 K.19 An exceptionally high measurement accuracy of 999.98‰, coupled with a post-aging drift rate of only 0.23% after 1000 hours, has been realized in the Ce1−2x(NdSm)x(VNbTa)1/3O4+δ system.20 Despite significant progress in existing studies, a critical issue pertaining to RENbO4-based ceramics involves structural phase transitions and nonstoichiometry during heating/cooling cycles, which can degrade electrical response consistency and long-term reliability. Furthermore, a systematic description and in-depth understanding of the thermal response mechanism and electro-thermal coupling behavior remain lacking.
Solid-solution strengthening, as an effective approach for modulating the structure and properties of ceramic materials, has been widely applied in functional ceramic systems.21,22 For RENbO4 materials, a phase transition to the tetragonal scheelite structure may occur under high-temperature conditions. This process is typically accompanied by a reduction in coordination number and an increase in unit cell symmetry within the crystal structure, thereby enhancing the material's structural stability and thermodynamic stability range.16,23,24 Stabilizing the fergusonite structure by introducing scheelite structural features via solid-solution strategies can effectively suppress structural distortion, delay the onset temperature of phase transformation, and further broaden the applicable temperature range for thermosensitive applications. For instance, Lin et al. successfully stabilized the fergusonite structure via solid solution of CaWO4 with Ce0.5La0.5NbO4, elevating the localized–delocalized transition temperature to a higher range and consequently optimizing the high-temperature resistance-temperature response characteristics.25 Furthermore, the “pinning effect” induced by a secondary phase resulting from defect engineering or compositional modulation has also been demonstrated to effectively inhibit abnormal grain growth and defect evolution.26 This inhibition enhances the thermo-structural stability and long-term service reliability of the ceramics. This design strategy has found extensive application across various domains.27–29 These findings suggest that the rational construction of fergusonite–scheelite solid solution ceramics, combined with the second-phase “pinning effect”, holds promise for stabilizing the crystal structure at the microscopic scale and improving long-term service reliability of RENbO4 ceramics.
Ca–Ce–Nb–Mo–O-based ceramics uniquely integrate the Ce4+/Ce3+ redox couple/oxygen vacancy chemistry with a thermally robust Nb/Mo d0 framework,30–32 enabling stable and tunable electrical transport behavior for high-temperature thermosensitive applications. Herein, we designed and constructed a CaCe2Nb2MoO12 ceramic with a high configurational entropy mixed-phase structure by synergistic modulation of composition and microstructure as shown in Fig. 1a. During the furnace cooling process after sintering, the cubic CeO2 phase was spontaneously precipitated at the interstices of grain boundaries, establishing stable heterogeneous interface structures. This configuration concurrently modulated the band structure and oxygen vacancy defect concentration to a certain extent, thereby optimizing electron transport behavior. Subsequent B-site modulation was conducted by substituting Nb5+ with Ta5+ in the CaCe2Nb2MoO12 lattice. This targeted substitution induces local lattice distortion and alters the Nb–O/Mo–O coordination environment, leading to the enhanced resistivity, stabilized material constants (B-values), and consequently improving thermal sensing performance. The resulting solid-solution strengthened ceramic demonstrates exceptional temperature sensitivity and measurement accuracy across a broad temperature range (153–773 K), along with rapid dynamic response characteristics. These attributes collectively satisfy the dual requirements for response speed and long-term stability in practical high-temperature sensing applications. This work provides new insights into the designable construction of high-performance, high-stability thermosensitive ceramic materials.
2. Experimental section
2.1 Materials preparation
CaMoO4 (CM), CaCeNbMoO8 (CCNM), and CaCe2Nb2−xTaxMoO12 (CC2N2M-xTa, x = 0.0, 0.1, 0.3, 0.5) ceramics were synthesized via a two-step sintering method33 using starting powders of CaCO3 (99.0%, Sinopharm), CeO2 (99.99%, Aladdin), Nb2O5 (99.99%, Sinopharm), MoO3 (99.5%, Sinopharm), and Ta2O5 (99.99%, Sinopharm). Raw materials were weighed according to stoichiometric ratios and mixed via ball milling for 8 h. The resultant slurries were dried and subsequently calcined at 1373 K for 6 h. The powders were then re-dispersed by ball milling and pressed into pellets approximately 10 mm in diameter and 2.0 mm thick under a uniaxial pressure of 20 MPa. Cold isostatic pressing (CIP) was applied at 300 MPa for 300 s to enhance the green density. Finally, the green bodies were heated to 1673 K at a rate of 3 K min−1, followed by cooling to 1473 K at 2 K min−1 and holding for 12 h. For comparison, pure CaMoO4 was first heated to 1523 K and then held at 1353 K for 12 h under similar sintering protocols.2.2 Materials characterization
Room-temperature X-ray diffraction (XRD) patterns of polycrystalline samples were recorded using a Bruker D8 Advance diffractometer with Cu Kα radiation. Data were collected over a 2θ range of 10° to 80° with a step size of 0.02° and a counting time of 3 s per step. Rietveld refinement of the XRD patterns was performed using TOPAS software to determine the crystal structure and phase composition. Ultraviolet-visible (UV-Vis) diffuse reflectance and absorption spectra were obtained using a Shimadzu UV 3600 Plus spectrophotometer equipped with a 20 nm slit and a barium sulfate (BaSO4) integrating sphere, covering a wavelength range of 190–2600 nm. Room-temperature Raman spectra were recorded under ambient conditions using a LABRAM HR Evolution micro-Raman spectrometer equipped with a 532 nm laser. Variable-temperature Raman spectra were collected in air using a Thermo Fisher Scientific DXR3xi ultra-fast confocal Raman imaging spectrometer equipped with a solid-state 532 nm laser (<30 mW). X-ray photoelectron spectroscopy (XPS) measurements were performed using a K-Alpha XPS spectrometer (Thermo Scientific K-Alpha, East Grinstead, UK). All spectra were referenced to the C 1s peak at a binding energy of 284.8 eV. The thermal conductivity was calculated by κ = DCpρ, where the thermal diffusivity (D) was measured by a laser flash method (Netzsch LFA467), the specific heat capacity (Cp) was calculated by Dulong–Petit law including thermal expansion effect, and the density (ρ) was measured by the Archimedes method, and Cp was estimated from the Dulong–Petit law (Cv ≈ 24.943 J mol−1 K−1 ≈ 3R per atom) and amended using literature-based parameters (α ≈ 1 × 10−5 K−1, B ≈ 100 GPa for RENbO4-type ceramics34–36) according to Cp = Cv + α2BTV.37,38 This approximation incorporates the effect of lattice thermal expansion but may still differ from true Cp at elevated temperatures. The microstructure and composition of the ceramics were examined using field-emission scanning electron microscopy (FE-SEM; Zeiss Supra 55 VP). Sample preparation for transmission electron microscopy involved thinning using a Helios G4 PFIB HXe focused ion beam scanning electron microscope equipped with a 2.5 µA xenon plasma FIB column. Microstructural characterization was conducted using an FEI Talos F200X aberration-corrected scanning transmission electron microscope operated at an accelerating voltage of 300 kV. Electron energy-loss spectroscopy (EELS) scan data were acquired across different regions within an energy range of 400 to 600 eV (O K-edge). Strain analysis from STEM-HAADF images was performed using a commercial geometric phase analysis (GPA) software package. Impedance spectroscopy measurements were carried out using an impedance analyzer (Wayne Kerr, WK6500) over a frequency range of 20 Hz to 10 MHz and a temperature range of 213–333 K. The obtained impedance spectra were analyzed by fitting with a 2RC equivalent circuit model, which consists of two parallel RC elements connected in series. In this model, the high-frequency and low-frequency semicircles correspond to the grain and grain boundary resistances, respectively.2.3 Performance testing
3. Results and discussion
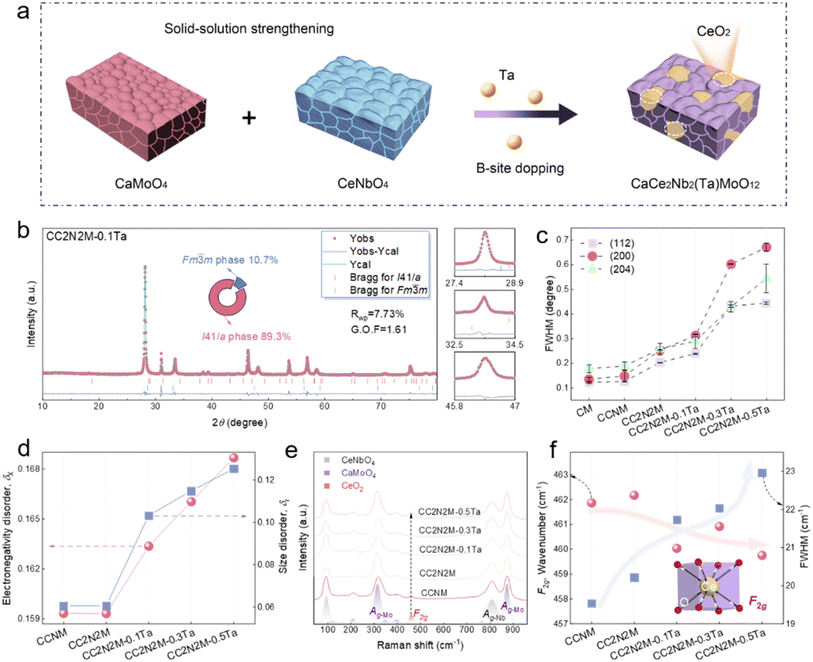
The crystal structures and morphologies of CM, CCNM, CC2N2M, CC2N2M-0.1Ta, CC2N2M-0.3Ta, and CC2N2M-0.5Ta ceramics were examined using X-ray diffraction (XRD), scanning electron microscopy (SEM), and Raman spectroscopy (Fig. 1). This characterization aimed to elucidate the development of thermosensitive performance through solid-solution strengthening and modification of the B-site composition. The XRD pattern of CM revealed a pure scheelite structure without impurities (Fig. S1, SI). Upon incorporation of CeNbO4 into the CaMoO4 lattice via solid-solution strengthening, all XRD patterns (CCNM, CC2N2M, CC2N2M-0.1Ta, CC2N2M-0.3Ta, and CC2N2M-0.5Ta) were indexed as a mixture of the scheelite and the cubic fluorite phases. This observation indicates that excess Ce could not be successfully incorporated into the CaMoO4 lattice to form a single-phase solid solution. Direct evidence for this phase separation is provided by the SEM images of the samples (Fig. S2, SI), where precipitated CeO2 particles exhibited surface morphologies distinctly different from the primary phase. To further confirm structural evolution, Rietveld refinement of XRD data was performed for all samples, as shown in Fig. 1b and S3 (refinement results listed in Table S1, SI). Good agreement between the observed and calculated patterns confirms the coexistence of two phases within the ceramics, belonging to the I41/a (tetragonal) and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (cubic) space groups, respectively. An increasing trend in the full width at half maximum (FWHM) of the samples was noted with increasing solid solution content and Ta5+ doping level, as evidenced in Fig. 1c. This trend indicates that the solid solution strengthening effect between CaMoO4 and CeNbO4, coupled with the increased lattice distortion enhances as Ta5+ doping levels rise, reflecting the formation characteristics of a high-entropy state. Concurrently, tantalum may act as a phase separation promoter, facilitating the segregation of the CeO2 phase from the primary scheelite-type phase while itself remaining within the host lattice. Direct evidence of elemental distribution was provided by SEM elemental mapping and line scanning analyses (Fig. S4 and S5, SI). Furthermore, an interesting phenomenon was observed: the content of the secondary CeO2 phase initially decreased with increasing solid solution content (i.e., the CaMoO4
m (cubic) space groups, respectively. An increasing trend in the full width at half maximum (FWHM) of the samples was noted with increasing solid solution content and Ta5+ doping level, as evidenced in Fig. 1c. This trend indicates that the solid solution strengthening effect between CaMoO4 and CeNbO4, coupled with the increased lattice distortion enhances as Ta5+ doping levels rise, reflecting the formation characteristics of a high-entropy state. Concurrently, tantalum may act as a phase separation promoter, facilitating the segregation of the CeO2 phase from the primary scheelite-type phase while itself remaining within the host lattice. Direct evidence of elemental distribution was provided by SEM elemental mapping and line scanning analyses (Fig. S4 and S5, SI). Furthermore, an interesting phenomenon was observed: the content of the secondary CeO2 phase initially decreased with increasing solid solution content (i.e., the CaMoO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CeNbO4 ratio changing from 1
CeNbO4 ratio changing from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and subsequently increased with higher Ta doping levels. Calculations of the size disorder parameter (δS) and the electronegativity difference (δX) for the prepared materials (Fig. 1d and Table S2, SI) revealed a correlation with the variation in CeO2 phase content. This correlation indicates an intrinsic link between the change in CeO2 phase content and the parameters of size disorder and electronegativity.
2) and subsequently increased with higher Ta doping levels. Calculations of the size disorder parameter (δS) and the electronegativity difference (δX) for the prepared materials (Fig. 1d and Table S2, SI) revealed a correlation with the variation in CeO2 phase content. This correlation indicates an intrinsic link between the change in CeO2 phase content and the parameters of size disorder and electronegativity.
Subsequent fitting of the Raman spectra for the ceramics is presented in Fig. 1e. It should be noted that the primary phase constitutes a solid solution of CaMoO4 and CeNbO4; consequently, the measured Raman spectra encompass vibrational modes from at least these two phases. Compared with pure CM (Fig. S6, SI), Raman vibrational modes corresponding to both the primary phase and the secondary CeO2 phase could be resolved for all samples, further confirming the presence of CeO2. The intense and sharp peaks located at 318 and 874 cm−1 are assigned to the symmetric Ag-Mo Raman-active stretching vibration modes of the rigid [MoO4] units within the O–Mo–O bonds.39 The broad peak centered at 801 cm−1 corresponds to the non-degenerate symmetric stretching (Ag-Nb) of the Nb–O vibration.15 Peaks below 300 cm−1 are frequently interpreted as external modes, dependent on the displacement of A-site ions.15,39 The peak observed near 461 cm−1 can be attributed to the F2g symmetric vibrational mode characteristic of the fluorite structure, arising from the symmetric stretching vibration of eight-coordinated CeO8 units.40 As shown in Fig. 1f, both the peak position and full width at half maximum (FWHM) of the F2g peak exhibit an overall blueshift and broadening trend with increasing Ta5+ content, indicating enhanced structural disorder.41 This behavior aligns with the mechanism whereby substitution of Nb5+ by Ta5+ weakens the B–O covalent bond and increases the bond length.42 The peak position and FWHM of the Ag-Nb peak display a variation trend similar to that of the CeO2 content within the bulk phase (Fig. S7, SI). This observation suggests that alterations in the coordination environment of B-site ions (Ta5+/Nb5+) directly modulate the covalency of the B–O bonds, while the interfacial stress exerted by the secondary CeO2 phase further induces long-range disordering within the solid solution lattice.
Analysis of the band structure provides fundamental insight into the electrical properties of materials. The band gaps of all samples, determined according to the Kubelka–Munk method,43 are presented in Fig. 2a. Values of 2.75–2.85 eV were obtained for the CCNM and CC2N2M-xTa ceramics, while pure CM exhibited a band gap of 3.89 eV (Fig. S8a, SI). Similarly, the valence band positions for all samples were calculated using the linear extrapolation method (Fig. 2b and S8b, SI). The presence of intermediate band (IB) states between the Fermi level and the valence band was identified in CCNM and CC2N2M-xTa samples, an observation absent in CM. These IB states are formed by high-density oxygen vacancies within the band gap.44 Although typically exploited for capturing low-energy photons and influencing photocarrier dynamics, the IB can also function as an additional pathway for carrier transitions,45,46 thereby effectively regulating excitation and recombination behavior of carriers across bands. This mechanism consequently reduces activation energy and enhances electron transport efficiency at elevated temperatures.47,48 The existence of oxygen vacancies is directly evidenced by O K-edge electron energy loss near-edge structure (ELNES) and O 1s XPS spectra (Fig. 2c and S9, SI). Within the secondary CeO2 phase region, EELS revealed a strong pre-edge peak at approximately 532 eV, which progressively weakens across the grain boundary transition zone and ultimately vanishes in the primary phase region (Fig. S10, SI). This feature is characteristic of oxygen vacancies, arising from the excitation of O 1s core electrons to empty O 2p orbitals.49,50 Furthermore, the O 1s XPS spectra displayed a prominent peak at 531.7 eV, corresponding to oxygen vacancies within lattice defects.44 This signal intensity, accounting for 43% of the total oxygen signal, is consistently observed across all CCNM and CC2N2M-xTa samples, reflecting a substantial concentration of oxygen vacancies. Subsequent comparison of the electronic structures of CCNM and CC2N2M-xTa was conducted by combining XPS valence band (XPS-VB) analysis and diffuse reflectance spectroscopy (DRS). The band diagrams for CCNM and CC2N2M-xTa, illustrated in Fig. 2d, show that the band gap value initially decreased and then increased with increasing solid solution content and Ta5+ doping level. This trend correlates with the variation in CeO2 content, indicating that the formation of the intermediate band is closely linked to oxygen vacancy concentration, while reversible transformation between Ce4+/Ce3+ (analysis shown in Fig. S11, SI) modulates the density and distribution of localized energy states.
The resistance-temperature characteristics of thermosensitive ceramics exhibit a direct correlation with the linearity of the material's response function and stability within the operational temperature range. This necessitates an approximately linear relationship between the natural logarithm of resistivity (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ) and the reciprocal of absolute temperature (1000/T) over the predetermined temperature range, while performance stability during continuous temperature variations must be ensured through lattice structural stability and consistency in carrier mobility. As shown in Fig. 2e, the electrical conductivity of all samples decreased sharply with increasing temperature, demonstrating reliable negative temperature coefficient (NTC) behavior. Furthermore, the relationship between the natural logarithm of resistivity (ln
ρ) and the reciprocal of absolute temperature (1000/T) over the predetermined temperature range, while performance stability during continuous temperature variations must be ensured through lattice structural stability and consistency in carrier mobility. As shown in Fig. 2e, the electrical conductivity of all samples decreased sharply with increasing temperature, demonstrating reliable negative temperature coefficient (NTC) behavior. Furthermore, the relationship between the natural logarithm of resistivity (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ) and the reciprocal of absolute temperature (1000/T) for the thermosensitive ceramics conforms to the Arrhenius equation,51 described by:
ρ) and the reciprocal of absolute temperature (1000/T) for the thermosensitive ceramics conforms to the Arrhenius equation,51 described by:
ρ = ρ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kBT) = ρ0 exp(Ea/kBT) = ρ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(B/T) exp(B/T) | (1) |
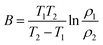 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ vs. 1000/T curve. Fig. 2g illustrates the variation of the B-value at different temperatures, revealing that Ta5+ doping results in a relatively smooth variation of B-value, indicating that the material has a high stability at varying temperatures. Meanwhile, the stability of the thermosensitive response was evaluated by analyzing the standard deviation (SD) and coefficient of variation (CV) of the B-value over the temperature range of 153–773 K. Lower SD and CV values signify the reduced fluctuation in the B-value and enhanced stability. The CC2N2M-0.3Ta exhibits the lowest SD and CV of the B-value (SD = 38.72, CV = 0.0105) within the temperature range of 153–773 K, demonstrating minimal fluctuations in activation energy and excellent thermal stability (Table S4, SI). Additionally, the thermal evolution of the local structure was resolved via in situ Raman spectroscopy, confirming the structural thermal stability of the CC2N2M-0.3Ta ceramic. As shown in Fig. 2h, deconvolution results demonstrated that the number of Raman peaks remained constant upon heating, suggesting the preservation of local symmetry over a wide temperature range. Fig. 2i and S13 (SI) show that typical Ag-Mo modes exhibited a gradual shift towards lower wavenumbers and an increase in full width at half maximum (FWHM) with temperature, indicating enhanced structural disorder.52,53 Conversely, the Ag-Nb vibrational mode fluctuates near 811.5 cm−1 and remains relatively stable, demonstrating temperature insensitivity (Fig. 2j). This implies that Nb–O bonds maintain a strong rigid structure throughout the temperature range, whereas Mo–O bonds exhibit relatively higher thermal sensitivity and a tendency for local distortion. Furthermore, the persistence of these vibrational modes across the entire tested temperature range indicates that the phase structure remains a stable scheelite phase without undergoing significant phase transformations. This stable phase structure facilitates consistent crystalline symmetry and local structural continuity from room temperature to high temperature, thereby ensuring the consistency of thermosensitive performance and the reliability of the response characteristics. Consequently, synthesizing the aforementioned results, it is reasonable to hypothesize that solid-solution strengthening combined with modification of the B-site composition effectively regulates the electronic states and operational stability of the material.
ρ vs. 1000/T curve. Fig. 2g illustrates the variation of the B-value at different temperatures, revealing that Ta5+ doping results in a relatively smooth variation of B-value, indicating that the material has a high stability at varying temperatures. Meanwhile, the stability of the thermosensitive response was evaluated by analyzing the standard deviation (SD) and coefficient of variation (CV) of the B-value over the temperature range of 153–773 K. Lower SD and CV values signify the reduced fluctuation in the B-value and enhanced stability. The CC2N2M-0.3Ta exhibits the lowest SD and CV of the B-value (SD = 38.72, CV = 0.0105) within the temperature range of 153–773 K, demonstrating minimal fluctuations in activation energy and excellent thermal stability (Table S4, SI). Additionally, the thermal evolution of the local structure was resolved via in situ Raman spectroscopy, confirming the structural thermal stability of the CC2N2M-0.3Ta ceramic. As shown in Fig. 2h, deconvolution results demonstrated that the number of Raman peaks remained constant upon heating, suggesting the preservation of local symmetry over a wide temperature range. Fig. 2i and S13 (SI) show that typical Ag-Mo modes exhibited a gradual shift towards lower wavenumbers and an increase in full width at half maximum (FWHM) with temperature, indicating enhanced structural disorder.52,53 Conversely, the Ag-Nb vibrational mode fluctuates near 811.5 cm−1 and remains relatively stable, demonstrating temperature insensitivity (Fig. 2j). This implies that Nb–O bonds maintain a strong rigid structure throughout the temperature range, whereas Mo–O bonds exhibit relatively higher thermal sensitivity and a tendency for local distortion. Furthermore, the persistence of these vibrational modes across the entire tested temperature range indicates that the phase structure remains a stable scheelite phase without undergoing significant phase transformations. This stable phase structure facilitates consistent crystalline symmetry and local structural continuity from room temperature to high temperature, thereby ensuring the consistency of thermosensitive performance and the reliability of the response characteristics. Consequently, synthesizing the aforementioned results, it is reasonable to hypothesize that solid-solution strengthening combined with modification of the B-site composition effectively regulates the electronic states and operational stability of the material.
To better understand the influence of Ta5+ doping on the microstructure and physical properties within solid solution strengthened systems, high-angle annular dark-field (HAADF) imaging and atomic-resolution X-ray energy-dispersive spectroscopy (EDS) analysis were performed using scanning transmission electron microscopy (STEM) across various scales and regions. Fig. 3a and S14 (SI) present the detailed STEM images of grains and grain boundary regions in two distinct areas for CC2N2M and CC2N2M-0.3Ta ceramics, respectively. The a secondary CeO2 phase possessing the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure was identified in both samples (insets, Fig. 3a and S14, SI), which further corroborates previous findings. A distinct grain boundary transition zone is evident between these two phases. This indicates that the introduction of the CeO2 secondary phase not only leads to independent precipitation within the grains but also triggers local interfacial reactions and structural reconstruction at the grain boundaries with the matrix phase, resulting in the formation of a compositional gradient and a stress transition layer. Atomic arrangements along the [011] zone axis are displayed in Fig. 3b and c. A noticeable increase in atomic spacing is observed following Ta5+ doping. Furthermore, the angle between the (0−11) and (002) planes increases from 85.2° to 88.1°, indicating significant local lattice distortion. This observation directly aligns with prior XRD results, where the diffraction peaks progressively broadened with increasing Ta content (Fig. 1c and S1, SI). To verify the local crystal strain variations induced by ion doping, geometric phase analysis (GPA) was conducted at the atomic scale (insets, Fig. 3b and c). The CC2N2M-0.3Ta ceramic exhibits characteristic nanoscale aggregation regions compared to CC2N2M, and the strain distribution fluctuations calculated by GPA are also much greater (Fig. S15, SI), signifying higher strain intensity and stronger strain fluctuations. This phenomenon arises because the atomic size mismatch in the Ta5+-doped sample is less easily accommodated by simple unit cell volume changes. Additionally, atomic off-centering caused by asymmetric potentials and distributions leads to distorted unit cells and substantial shear strain.54 An atomic-resolution HAADF image of the precipitated secondary CeO2 phase within the CC2N2M-0.3Ta ceramic is presented in Fig. S16 (SI). The triangular region was utilized for quantitative lattice mismatch analysis. The measured spacings and intensity profiles (a–b, m–n, x–y) reveal significant lattice misfit, indicating a semi-coherent interface characterized by interfacial strain.
m structure was identified in both samples (insets, Fig. 3a and S14, SI), which further corroborates previous findings. A distinct grain boundary transition zone is evident between these two phases. This indicates that the introduction of the CeO2 secondary phase not only leads to independent precipitation within the grains but also triggers local interfacial reactions and structural reconstruction at the grain boundaries with the matrix phase, resulting in the formation of a compositional gradient and a stress transition layer. Atomic arrangements along the [011] zone axis are displayed in Fig. 3b and c. A noticeable increase in atomic spacing is observed following Ta5+ doping. Furthermore, the angle between the (0−11) and (002) planes increases from 85.2° to 88.1°, indicating significant local lattice distortion. This observation directly aligns with prior XRD results, where the diffraction peaks progressively broadened with increasing Ta content (Fig. 1c and S1, SI). To verify the local crystal strain variations induced by ion doping, geometric phase analysis (GPA) was conducted at the atomic scale (insets, Fig. 3b and c). The CC2N2M-0.3Ta ceramic exhibits characteristic nanoscale aggregation regions compared to CC2N2M, and the strain distribution fluctuations calculated by GPA are also much greater (Fig. S15, SI), signifying higher strain intensity and stronger strain fluctuations. This phenomenon arises because the atomic size mismatch in the Ta5+-doped sample is less easily accommodated by simple unit cell volume changes. Additionally, atomic off-centering caused by asymmetric potentials and distributions leads to distorted unit cells and substantial shear strain.54 An atomic-resolution HAADF image of the precipitated secondary CeO2 phase within the CC2N2M-0.3Ta ceramic is presented in Fig. S16 (SI). The triangular region was utilized for quantitative lattice mismatch analysis. The measured spacings and intensity profiles (a–b, m–n, x–y) reveal significant lattice misfit, indicating a semi-coherent interface characterized by interfacial strain.
Additionally, the effects of Ta5+ doping on lattice distortion were evaluated. As illustrated in Fig. 3d–k, the measured lattice distortion, manifested as positional displacements of atomic sites, increased significantly following doping. Based on the average displacement of matrix phase atoms determined by the method of displacement separation analysis55 (details in Fig. S17, SI), a substantial increase from 6.67 pm for CC2N2M ceramic (Fig. 3f) to 7.95 pm for CC2N2M-0.3Ta ceramic (Fig. 3j) was observed. This result indicates that the incorporation of Ta5+ significantly enhances the configurational entropy of the system, consequently exacerbating lattice disorder.56,57 Beyond the measurements of atomic displacement within two-dimensional planes, the atomic column intensity of the materials was also calculated. As shown in Fig. 3g and k, the average atomic column intensity at atomic sites increased from ∼2.24 × 104 for CC2N2M to ∼2.41 × 104 for the CC2N2M-0.3Ta sample. This further confirms the enhanced disorder within the Ta5+-doped structure. Concurrently, the distribution range of atomic column intensities broadened significantly, directly reflecting that elemental fluctuations induced by the Ta dopant lead to considerable chemical disorder.58 The increase in atomic displacement, together with the broadened strength distribution of atomic columns, is a typical characteristic of heightened chemical disorder and localized lattice distortion in high-entropy materials. Finally, STEM-EDS elemental mapping elucidates the spatial distribution of the principal elements within the samples (Fig. 3l and S18, SI). Ce is concentrated within the secondary phase regions, consistent with the identification as CeO2. In contrast, Ta within the CC2N2M-0.3Ta ceramic is uniformly distributed throughout the host lattice, confirming its incorporation via doping. These results demonstrate that defect structures and interfacial strain play crucial roles in modulating charge carrier behavior and band structure, thereby enhancing the thermosensitive properties of the ceramics.
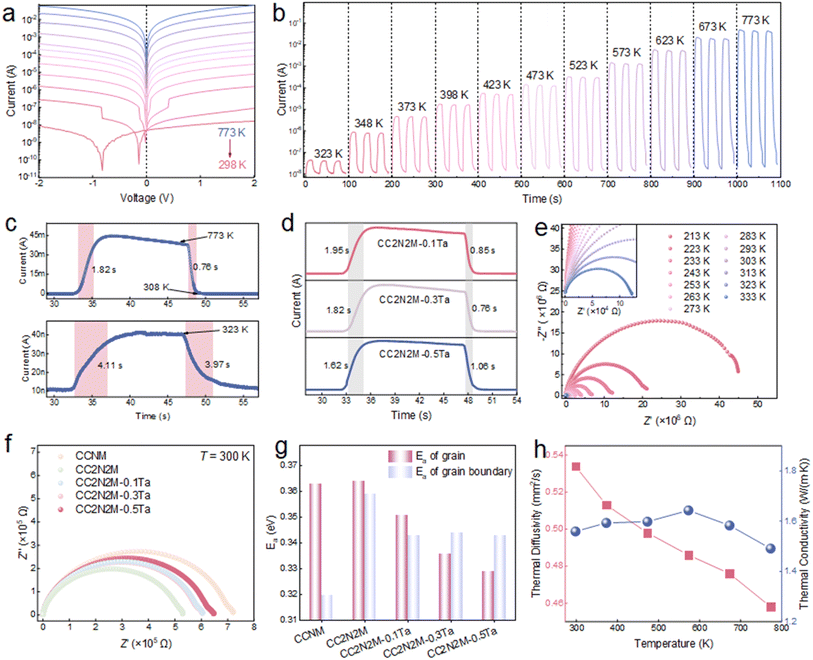
Subsequent investigation focused on the current–voltage (I–V) characteristics, sensitivity, and response time of CC2N2M-xTa ceramics. Using the CC2N2M-0.3Ta ceramic as an example, a very low current (approximately 10 nA at 2 V) was recorded at room temperature, as illustrated in Fig. 4a. Simultaneously, highly symmetric I–V curves were observed under both forward and reverse biases at elevated temperatures, indicating sufficient thermally excited charge carriers and dominance of current by thermal emission. In contrast, a significant zero-point shift and low symmetry were evident at low temperatures, potentially attributable to the larger resistivity of the ceramic and the differing degrees of space-charge region expansion under forward and reverse bias conditions at reduced temperatures. A gradual increase in current magnitude was observed with rising temperature, reaching a maximum value of approximately 0.1 A at 773 K, representing an increase of eight orders of magnitude (Fig. 4b). Notably, the room temperature resistance was approximately 100 MΩ, which could be reduced by employing smaller electrode spacings or a reduced thermosensitive volume. The temperature dependence of R/R0 for CC2N2M-0.3Ta ceramic over a broad temperature range from 153 K to 773 K is presented in Fig. S19 (SI). This extensive temperature range, continuously covering variations from cryogenic to high temperatures, enables the testing of reliability for electronic components, aerospace parts, and automotive materials under extreme thermal cycling, making accurate temperature measurement crucial. Correspondingly, the B-value and temperature coefficient at 773 K for CC2N2M-0.3Ta ceramic were determined to be 3833 K and 0.641% K−1, respectively (Fig. 2f). The response times of CC2N2M-0.3Ta ceramic to thermal stimuli at low (323 K) and high (773 K) temperatures are shown in Fig. 4c. Faster response and recovery times were observed for the high-temperature stimulus compared to the low-temperature one. All Ta5+-doped compositions exhibited excellent response and recovery times (Fig. 4d), the response time progressively decreased as the Ta5+ doping concentration increased. This response time is significantly faster than that observed in other ion-migration type thermosensitive sensors.59–61
Complex impedance spectroscopy and thermal conductivity measurements provided deeper insights into the operational mechanism governing the temperature response across different temperatures. Cole–Cole plots depicting the resistance are presented in Fig. 4e and S20a (SI). The electrochemical impedance spectra were fitted using an equivalent circuit consisting of two R–C elements connected in series. The diameter of the semicircle gradually decreased with increasing temperature, indicating a reduction in the grain and grain boundary resistance of the sensor due to thermal elevation. This reduction is attributed to the enhanced electron mobility resulting from thermal excitation at higher temperatures. Furthermore, the complex impedance results for all ceramics at room temperature were compared, as shown in Fig. 4f. The total resistance initially decreased sharply with increasing solid solubility, followed by a gradual increase with Ta5+ doping, consistent with the resistance-temperature measurements (Fig. 2e). The influence of temperature on the grain/grain boundary resistance was described using the Arrhenius equation, illustrated in Fig. 4g and S20b (SI). The relationship between resistance and temperature conforms to the equation within the range of 213 K to 333 K, enabling the calculation of activation energies (Ea) for both grains and grain boundaries. The Ea for grain boundaries exhibits a gradual decreasing trend with increasing Ta5+ doping content, while the Ea for grains remains relatively constant. This indicates that grain resistance progressively dominates with higher Ta5+ doping content. Due to the pinning effect of the secondary cubic CeO2 phase and the induced local lattice distortion, the stability of the defect barrier is effectively enhanced. Consequently, the ceramic microstructure becomes more dense and uniform, the constraint on carrier scattering paths was reduced, and the consistency of electrical transport properties and temperature response is further improved. Thermal conductivity and thermal diffusivity measurement results for the CC2N2M-0.3Ta ceramic are displayed in Fig. 4h. The thermal conductivity exhibits minimal variation and remains relatively stable overall as temperature increases. In contrast, the thermal diffusivity demonstrates a gradual decreasing trend. This behavior contrasts distinctly with the experimental observation of faster response times at elevated temperatures (4.11 s at 323 K vs. 1.82 s at 773 K). This phenomenon suggests that the dominant heat transfer mechanism governing the response process is not solely dependent on the intrinsic solid thermal conduction behavior. Notably, the heat transfer efficiency of thermal radiation is a strong function of temperature (∝T4), and its contribution to energy transport becomes significantly enhanced at high temperatures.62,63 Therefore, even though the material's thermal conductivity and thermal diffusivity show insignificant change or a slight decrease with temperature, the total heat flux dominated by radiation increases markedly at high temperatures. This accelerates the rate of heat transfer from the external environment into the sensitive element region, thereby shortening the response time. In other words, the accelerated thermal response at high temperatures primarily benefits from the enhanced contribution of radiative heat transfer, compensating for the deficit in solid thermal conduction capability.
4. Conclusion
The CC2N2M-xTa ceramic system provides an efficient platform for tuning high-temperature thermosensitive performance. Through a multi-strategy design integrating solid-solution-induced lattice reinforcement, Nb/Ta ratio adjustment, and entropy-driven structural disorder, the optimized CC2N2M-0.3Ta composition delivers near-ideal linear thermoresistive behavior (R2 = 0.99945) in the temperature of 153–773 K and a rapid thermoresistive response of 1.82 s at 773 K. Atomic-scale analyses reveal pronounced lattice distortion and semi-coherent interfaces within the CC2N2M-0.3Ta ceramic, mechanistically linked to its superior thermal sensitivity and stability. The composition further exhibits excellent structural integrity and a radiation-influenced heat-transfer pathway that compensates for reduced thermal diffusivity, collectively ensuring reliable operation across a wide temperature range. These findings clarify the structural origins underpinning the enhanced thermoresistive behavior and establish the fergusonite-type ceramics as a promising candidate for high-performance, wide-temperature-range thermosensitive sensors.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
Other data are made accessible through reasonable requests to the corresponding authors.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: XRD refinement parameters, electronegativity and size disorder calculations, thermosensitive parameter statistics, XRD patterns and refinements, SEM/EDS microstructural analyses, Raman, XPS and EELS characterizations, TEM and strain-mapping results, and temperature-dependent electrical and impedance measurements. See DOI: https://doi.org/10.1039/d5ta06147d.
Acknowledgements
We would like to acknowledge financial support from the National Natural Science Foundation of China (Grant No. 62471468), the Youth Innovation Promotion Association of CAS (Grant No. Y2023117), Natural Science Foundation of Xinjiang (Grant No. 2024D01E32), Xinjiang Tianshan Talent Training Program (Grant No. 2023TSYCCX0092), and the Science and Technology Development Project of Two Zones of XinJiang (Grant No. 2022LQ03006).References
- F. F. Chen, Y. J. Zhu, F. Chen, L. Y. Dong, R. L. Yang and Z. C. Xiong, ACS Nano, 2018, 12, 3159–3171 CrossRef CAS
.
- A. Pal, K. C. Lim, S. W. Chen, Y. T. Huang, P. Parashar, A. Ganguly, Y. H. Chen, K. P. Fan, L. C. Shen, J. Cheng and Z.-H. Lin, Device, 2024, 2, 100421 CrossRef
.
- Z. Liu, B. Tian, B. Zhang, J. Liu, Z. Zhang, S. Wang, Y. Luo, L. Zhao, P. Shi, Q. Lin and Z. Jiang, Microsyst. Nanoeng., 2021, 7, 42 CrossRef CAS PubMed
.
- S. Hao, R. Dai, Q. Fu, Y. Wang, X. Zhang, H. Li, X. Liu and J. Yang, Adv. Funct. Mater., 2023, 33, 2302840 CrossRef CAS
.
- Z. Hu, D. Qiu, J. Zhao, X. Peng and H. Peng, Energy Convers. Manage., 2024, 312, 118566 CrossRef
.
- A. Wang, Q. Li, F. Cao and D. Hu, J. Cleaner Prod., 2024, 434, 140208 CrossRef CAS
.
- X. Zhao, G. Chen, H. Liu and L. Wang, IEEE Trans. Instrum. Meas., 2022, 71, 1–12 Search PubMed
.
- S. Sahoo, S. K. S. Parashar and S. M. Ali, J. Adv. Ceram., 2014, 3, 117–124 CrossRef CAS
.
- D. Houivet, J. Bernard and J.-M. Haussonne, J. Eur. Ceram. Soc., 2004, 24, 1237–1241 CrossRef CAS
.
- R. Wu, Z. Fu, Y. Liu, Y. Wei, H. Sun, A. Chang and B. Zhang, J. Alloys Compd., 2024, 973, 172908 CrossRef CAS
.
- J. Li, F. Pan, S. Geng, C. Lin, L. Palatinus, M. Allix, X. Kuang, J. Lin and J. Sun, Nat. Commun., 2020, 11, 4751 CrossRef CAS
.
- K. Toyoura, Y. Sakakibara, T. Yokoi, A. Nakamura and K. Matsunaga, J. Mater. Chem. A, 2018, 6, 12004–12011 RSC
.
- R. B. Jordan, Inorg. Chem., 2023, 62, 3715–3721 CrossRef CAS PubMed
.
- R. J. Ellis, D. M. Brigham, L. Delmau, A. S. Ivanov, N. J. Williams, M. N. Vo, B. Reinhart, B. A. Moyer and V. S. Bryantsev, Inorg. Chem., 2017, 56, 1152–1160 CrossRef CAS PubMed
.
- K. P. F. Siqueira, R. L. Moreira and A. Dias, Chem. Mater., 2010, 22, 2668–2674 CrossRef CAS
.
- A. B. Garg, R. Rao, D. Errandonea, J. Pellicer-Porres, D. Martinez-Garcia and C. Popescu, J. Appl. Phys., 2020, 127, 175905 CrossRef CAS
.
- Z. Zheng, H. Ji, Y. Zhang, J. Cai and C. Mo, Solid State Ionics, 2022, 377, 115872 CrossRef CAS
.
- H. Sun, Y. Wang, Y. Liu, R. Wu, A. Chang, P. Zhao and B. Zhang, ACS Appl. Mater. Interfaces, 2024, 16, 12821–12832 CrossRef CAS
.
- H. Sun, J. Xu, R. Wu, J. Chen, Y. Liu, K. Li, A. Chang and B. Zhang, Small, 2025, 21, 2408952 CrossRef CAS
.
- Y. Liu, R. Wu, H. Sun, A. Chang, J. Guo and B. Zhang, ACS Appl. Mater. Interfaces, 2024, 16, 28861–28873 CrossRef CAS PubMed
.
- J. Fu, Z. Yu, A. Xie, Z. Yu, Z. Fu, X. Jiang, T. Li and R. Zuo, Acta Mater., 2023, 254, 118991 CrossRef CAS
.
- P. E. Albert, C. J. Ryan, E. T. Furton, R. Sweny, M. P. Galaini, R. J. Crealese, P. A. Kolonin, A. M. Beese and D. E. Wolfe, J. Eur. Ceram. Soc., 2024, 44, 6827–6838 CrossRef CAS
.
- Yu. A. Titov, A. M. Sych, A. N. Sokolov, V. Ya. Markiv, N. M. Belyavina and A. A. Kapshuk, High Pressure Res., 2001, 21, 175–181 CrossRef
.
- J. Hou, R. Zhou, J. Zhang, Z. Wang, Z. Zhang and Z. Ding, J. Phys. Chem. C, 2017, 121, 14787–14794 CrossRef CAS
.
- Y. Lin, J. Shi, W. Zhou, W. Cen, A. Chang and B. Zhang, Appl. Phys. Lett., 2022, 120, 112106 CrossRef CAS
.
- P. Li, S. Wang, J. Qian, G. Ge, L. Tang, J. Lin, W. Yang, J. Lin, W. Lin, B. Shen and J. Zhai, Chem. Eng. J., 2024, 497, 154926 CrossRef CAS
.
- C. Zhou, L. Li, Z. Dong, F. Lv, H. Guo, K. Wang, M. Li, Z. Qian, N. Ye, Z. Lin, M. Luo and S. Guo, Nat. Commun., 2024, 15, 9774 CrossRef CAS PubMed
.
- J. Li, X. Zhao, P. He, Y. Liu, J. Jin, Q. Shen, Y. Wang, S. Li, X. Qu, Y. Liu and L. Jiao, Small, 2022, 18, 2202879 CrossRef CAS
.
- S. Chu, C. Zhang, H. Xu, S. Guo, P. Wang and H. Zhou, Angew. Chem., Int. Ed., 2021, 60, 13366–13371 CrossRef CAS PubMed
.
- B. Zhang, Q. Zhao, C. Zhao and A. Chang, J. Alloys Compd., 2017, 698, 1–6 CrossRef CAS
.
- K. Ravindran Nair, P. Prabhakar Rao, S. Sameera, V. S. Mohan, M. R. Chandran and P. Koshy, Mater. Lett., 2008, 62, 2868–2871 CrossRef CAS
.
- M. Deepa, P. P. Rao, S. Sumi, A. N. P. Radhakrishnan and P. Koshy, J. Am. Ceram. Soc., 2010, 93, 1576–1579 CrossRef CAS
.
- X. Li, L. Zhang, Y. Dong, R. Gao, M. Qin, X. Qu and J. Li, Acta Mater., 2020, 186, 116–123 CrossRef CAS
.
- L. Lai, M. Gan, J. Wang, L. Chen, X. Liang, J. Feng and X. Chong, J. Am. Ceram. Soc., 2023, 106, 4343–4357 CrossRef CAS
.
- Z. Yu, D. Hu, F. Cai, Y. Wu, W. Wen and T. Chen, Mater. Today Commun., 2025, 48, 113637 CrossRef CAS
.
- J. Tian, J. Zhu, J. Zheng, Y. Li, K. Yang, M. Li, H. Wang and J. He, Appl. Surf. Sci., 2025, 688, 162315 CrossRef CAS
.
- N. Boukhris, H. Meradji, S. A. Korba, S. Drablia, S. Ghemid and F. El Haj Hassan, Bull. Mater. Sci., 2014, 37, 1159–1166 CrossRef CAS
.
- M. Cardona, R. K. Kremer, R. Lauck, G. Siegle, J. Serrano and A. H. Romero, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 075211 CrossRef
.
- S. P. S. Porto and J. F. Scott, Phys. Rev., 1967, 157, 716–719 CrossRef CAS
.
- D. Kang, X. Yu and M. Ge, Chem. Eng. J., 2017, 330, 36–43 CrossRef CAS
.
- T. Wei, J. Zou, X. Zhou, M. Song, Y. Zhang, C. Nan, Y. Lin and D. Zhang, Nat. Commun., 2025, 16, 807 CrossRef CAS PubMed
.
- J. Liu, Y. Jiang, W. Zhang, X. Cheng, P. Zhao, Y. Zhen, Y. Hao, L. Guo, K. Bi and X. Wang, Nat. Commun., 2024, 15, 8651 CrossRef CAS PubMed
.
- P. Kubelka and F. Munk, Zeitschrift für Technische Physik, 1931, 12, 593–609 Search PubMed
.
- H. Ling, H. Sun, L. Lu, J. Zhang, L. Liao, J. Wang, X. Zhang, Y. Lan, R. Li, W. Lu, L. Cai, X. Bai and W. Wang, Nat. Commun., 2024, 15, 9505 CrossRef CAS PubMed
.
- S. Selim, E. Pastor, M. García-Tecedor, M. R. Morris, L. Francàs, M. Sachs, B. Moss, S. Corby, C. A. Mesa, S. Gimenez, A. Kafizas, A. A. Bakulin and J. R. Durrant, J. Am. Chem. Soc., 2019, 141, 18791–18798 CrossRef CAS PubMed
.
- W. Jiang, H. Loh, B. Q. L. Low, H. Zhu, J. Low, J. Z. X. Heng, K. Y. Tang, Z. Li, X. J. Loh, E. Ye and Y. Xiong, Appl. Catal., B, 2023, 321, 122079 CrossRef CAS
.
- E. Garduno-Nolasco, M. Missous, D. Donoval, J. Kovac and M. Mikolasek, J. Semicond., 2014, 35, 054001 CrossRef CAS
.
- N. López, L. A. Reichertz, K. M. Yu, K. Campman and W. Walukiewicz, Phys. Rev. Lett., 2011, 106, 028701 CrossRef
.
- D. A. Muller, N. Nakagawa, A. Ohtomo, J. L. Grazul and H. Y. Hwang, Nature, 2004, 430, 657–661 CrossRef CAS
.
- Z. Dong, M. Huo, J. Li, J. Li, P. Li, H. Sun, L. Gu, Y. Lu, M. Wang, Y. Wang and Z. Chen, Nature, 2024, 630, 847–852 CrossRef CAS PubMed
.
- A. Feteira, J. Am. Ceram. Soc., 2009, 92, 967–983 CrossRef CAS
.
- J. Duan, K. Wei, Q. Du, L. Ma, H. Yu, H. Qi, Y. Tan, G. Zhong and H. Li, Nat. Commun., 2024, 15, 6754 CrossRef CAS
.
- A. Xie, R. Zuo, Z. Qiao, Z. Fu, T. Hu and L. Fei, Adv. Energy Mater., 2021, 11, 2101378 CrossRef CAS
.
- B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, Science, 2021, 371, 830–834 CrossRef CAS PubMed
.
- Y. Zhang, R. Yu and J. Zhu, Ultramicroscopy, 2022, 232, 113404 CrossRef CAS PubMed
.
- N. Dragoe and D. Bérardan, Science, 2019, 366, 573–574 CrossRef CAS PubMed
.
- S. S. Aamlid, M. Oudah, J. Rottler and A. M. Hallas, J. Am. Chem. Soc., 2023, 145, 5991–6006 CrossRef CAS PubMed
.
- W. Wang, S. Liu, Y. Wang, B. Jia, Y. Huang, L. Xie, B. Jiang and J. He, Sci. Adv., 2024, 10, eadp4372 CrossRef CAS
.
- X. Zhao, J. Guo, J. Wang and Y. Yan, Small, 2023, 19, 2205136 CrossRef CAS PubMed
.
- M. Umar, F. S. Irani, S. S. Mirbakht and M. K. Yapici, Adv. Electron. Mater., 2024, 10, 2300723 CrossRef CAS
.
- J. Zou, Y. Ma, C. Liu, Y. Xie, X. Li, S. Li, S. Peng, Y. Yue, C.-W. Nan, X. Zhang, X. Dai and S. Wang, InfoMat, 2024, 6(7), e12545 Search PubMed
.
- H. Li, L. J. Fernández-Alcázar, F. Ellis, B. Shapiro and T. Kottos, Phys. Rev. Lett., 2019, 123, 165901 CrossRef CAS
.
- A. Shahsafi, P. Roney, Y. Zhou, Z. Zhang, Y. Xiao, C. Wan, R. Wambold, J. Salman, Z. Yu, J. Li, J. T. Sadowski, R. Comin, S. Ramanathan and M. A. Kats, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 26402–26406 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2026 |