Accelerating the discovery of high-efficiency donor–acceptor pairs in organic photovoltaics via SolarPCE-Net guided screening
Xingyu
Liu
ab,
Bo
Hu
c,
Pei
Liu
d,
Meng
Huang
 *a,
Ming
Li
a,
Yuwei
Wan
ef,
Bram
Hoex
*a,
Ming
Li
a,
Yuwei
Wan
ef,
Bram
Hoex
 g and
Tong
Xie
g and
Tong
Xie
 fg
fg
aSchool of Computer Engineering, Jiangsu Ocean University, No. 59 Cangwu Road, Cangwu Campus, Lianyungang, 222005, China. E-mail: huangmeng@jou.edu.cn
bCollege of Resources and Environmental Sciences, Nanjing Agricultural University, No. 666, JiangPu Road, PuKou District, Nanjing, 210095, China
cGuilin University of Technology, No. 319, Yanshan Street, Yanshan District, Guilin, 541006, China
dThe Hong Kong University of Science and Technology (Guangzhou), No. 1, Duxue Road, Nansha District, Guangzhou, 511458, China
eDepartment of Linguistics and Translation, City University of Hong Kong, Hong Kong, China
fGreen Dynamics, Kensington, NSW, Australia
gSchool of Photovoltaic and Renewable Energy Engineering, University of New South Wales, Kensington, NSW, Australia
First published on 8th October 2025
Abstract
Organic photovoltaic (OPV) materials possess great potential for accelerating solar energy conversion. Rapid screening of high-performance donor–acceptor (D–A) materials helps reduce the cost and time consumption associated with traditional experimental trial-and-error methods. However, for predicting the power conversion efficiency (PCE) of D–A in OPV, the existing approaches focus on efficiency prediction of single-component materials and neglect synergistic D–A coupling effects critical to device performance. Here, we propose the Solar Power Conversion Efficiency Network (SolarPCE-Net), a novel deep learning-based framework for OPV material screening that captures the intricate dynamics within D–A pairs. By integrating a residual network with the self-attention mechanism, the SolarPCE-Net employs a dual-channel architecture to process molecular descriptor signatures of D–A while quantifying interfacial coupling effects through attention-weighted feature fusion. We apply the proposed method to the HOPV15 dataset. Experimental results show that our proposed SolarPCE-Net exhibits certain advantages in terms of accuracy and generalization ability compared to traditional methods. Interpretability analysis by attention weighting reveals key molecular descriptors that influence performance. Our work screens undeveloped D–A combinations, demonstrating its potential to accelerate high-performance OPV material discovery.
1. Introduction
Organic photovoltaic (OPV) materials, as promising green energy materials, can convert solar energy into electricity through the photovoltaic effect.1 Due to their low production cost, mechanical flexibility, and compatibility with large-area manufacturing processes, OPV materials have attracted significant attention in solar cell applications.2–4 Among the various performance metrics of OPV devices, power conversion efficiency (PCE) and long-term stability are obviously the most critical factors determining their commercial viability. Despite notable advances in molecular design and device engineering, the relatively low PCE of OPV devices remains a major bottleneck hindering large-scale application.5–8Traditionally, OPV material development heavily relies on physical models and empirical formulae.9–11 For example, the widely adopted Scharber model12 estimates the upper limit of PCE based on the energy levels of donor's highest occupied molecular orbital (HOMO) and acceptor's lowest unoccupied molecular orbital (LUMO). While such models offer valuable physical insights, they typically require extensive experimental measurements and computational simulations, which are time-consuming and inefficient for rapid screening of donor–acceptor (D–A) pair combinations in the vast chemical space of OPV materials. To overcome these challenges, machine learning (ML) has emerged as a powerful tool for establishing quantitative structure–property relationships (QSPRs) in OPV materials.13 The ML-based techniques can leverage existing experimental and computational datasets to efficiently map the relationship between molecular structures and photovoltaic performance, significantly reducing computational costs and accelerating material discovery. The ML-based techniques can leverage existing experimental and computational datasets to efficiently map the relationship between molecular structures and photovoltaic performance, significantly reducing computational costs and accelerating material discovery.44
In recent years, ML-based models reveal structure–performance patterns that may be difficult to capture through traditional physical models alone and guide material design, which have made significant progress in predicting the PCE of OPV materials.14 For example, Nagasawa et al.15 used a random forest classification model to achieve a four-class prediction of the optoelectronic conversion efficiency of OPV materials through molecular fingerprints and molecular orbital energy levels. Jørgensen et al.16 accurately predicted the LUMO energy levels and optical band gaps of molecules using machine learning regression models. Sun et al.17 processed a complex database containing various organic photovoltaic donor materials using a random forest algorithm and found that molecular fingerprints with lengths exceeding 1000 bits were the best input. Sahu et al.18 used micro-properties obtained from Density Functional Theory (DFT) calculations as inputs to predict the PCE of OPV materials, achieving a correlation coefficient of up to 0.79. Machine learning has emerged as a powerful tool for accelerating materials discovery by establishing predictive models between material properties and their structures. However, its widespread adoption in materials science often faces the significant challenge of limited experimental data, a prevalent issue that few-shot learning methods are increasingly addressing by enabling effective learning from scarce samples.45 Furthermore, deep learning-based methods have also shown great potential in this field. Sun et al.17 used convolutional neural networks (CNNs) and data from the Harvard Clean Energy Project (CEP) to predict the PCE, achieving a prediction accuracy of 91.02%, proving that CNNs can extract features from chemical structure images. Richards et al.19 proposed an attention-driven Long Short-Term Memory (LSTM) network that, using text descriptors and data augmentation techniques combined with self-attention mechanisms, can effectively predict the optoelectronic conversion efficiency of OPV materials. Chen et al.20 used a deep learning model combining Bi-LSTM networks, attention mechanisms, and backpropagation neural networks (BPNNs), encoding organic compound molecular structures with language-like molecular descriptors,21 innovatively applying natural language processing techniques to molecular descriptor processing and prediction. Huang et al. utilized a deep learning infrared holographic technique with a self-attention mechanism to solve the critical problem of high-fidelity phase disentanglement, providing in-depth insights into the characterization of new materials, crystal growth, and performance changes.46 Among these approaches, graph neural networks (GNNs) have emerged as a key technology due to their inherent suitability for molecular graph-structured data. For instance, Eibeck et al. conducted the first systematic comparison between GNNs and traditional ML models, demonstrating that their simple GNN architecture achieved high-precision PCE prediction (test set MSE = 0.091) solely based on atomic features, significantly outperforming conventional methods like random forests.47 To further enhance model generalization, Qiu et al. proposed a collaborative framework integrating pre-trained GNNs with reinforcement learning, enabling high-throughput screening of candidate molecules with PCE (predicted value ≈ 21%). They also constructed a large-scale open-source dataset to advance the field.48 Furthermore, expansions into crystalline materials—such as the GNNOpt model developed by Tohoku University and MIT—validated GNNs' universality in cross-scale material efficiency prediction, successfully identifying 246 novel photovoltaic materials with PCE > 32%.49 These advancements underscore GNNs' pivotal role in accelerating the discovery of high-performance organic photovoltaic materials.
However, the traditional physics-based methods, such as the Scharber model, rely on oversimplified linear assumptions, which fail to capture the non-linear interfacial dynamics, such as exciton dissociation, dipole alignment, and charge recombination that critically influence device performance. In addition, many existing ML-based PCE prediction models focus on either donor or acceptor molecules in isolation, neglecting the synergistic interactions between donor–acceptor pairs, which fundamentally determine device performance.22 Furthermore, although deep learning methods (e.g., CNNs and GNNs) have improved the extraction of molecular features from fingerprints or molecular graphs, they often struggle to capture long-range dependencies and complex hierarchical information within donor–acceptor systems.23 Specifically, conventional deep networks (CNNs and GNNs) tend to focus on local patterns or single-molecule characteristics without a general approach to modeling D–A pair synergies.24,25 This study learns the long-distance dependencies and complex interactions between two molecules through a series of attention-enhancing residual blocks, ensuring that D–A synergies are accurately captured.
In this work, we propose a novel Solar Power Conversion Efficiency Network (SolarPCE-Net) to predict the PCE value of D–A pairs. This SolarPCE-Net integrates the residual network extracting deep features and the self-attention mechanism to model the intricate relationships within D–A pairs. By focusing on the coupled characteristics of D–A systems, the SolarPCE-Net aims to bridge the existing gap between molecular-level descriptors and device-level performance. We construct a comprehensive dataset of donor–acceptor pairs from publicly available OPV material databases26 and scientific literature databases,27 enriched with molecular structures, energy levels, and optical properties. These extracted molecular descriptors are used as input for the proposed SolarPCE-Net. Extensive experiments and cross-validation show that the SolarPCE-Net outperforms several baseline models in terms of prediction accuracy and generalization capability. By interpretability analysis, the key molecular descriptors affecting PCE have been revealed, guiding material optimization. In addition, we also apply the proposed SolarPCE-Net to screen donor–acceptor pairs with higher PCE from unexplored D–A combinations, which accelerate the rapid screening of efficient OPV materials and advance solar cell technology. This work offers several important contributions: (1) a novel framework tailored for donor–acceptor pair modeling in OPV materials, addressing the material-level coupling effect often overlooked in the prior method. (2) A predictive model capable of facilitating rapid screening and design of high-performance OPV material pairs, thereby accelerating solar cell development. (3) Insights into critical factors (molecular descriptors) influencing PCE through interpretability analysis enabled by the self-attention mechanism.
2. Methods
To accelerate the screening of OPV materials, we have proposed the SolarPCE-Net to predict the PCE of D–A pairs. As shown in Fig. 1, our method contained four stages: (1) data collection and preprocessing, (2) feature extraction, (3) model training and PCE prediction and (4) result analysis. In the data collection and preprocessing stage, we used the HOPV15 dataset, which contains a rich set of donor–acceptor molecular pairs and their performance metrics. In the feature extraction stage, we applied two different encoding strategies: the MolSig program28 was used to generate molecular signature descriptors for donor molecules, while one-hot encoding was used to represent acceptor molecules. In the model training and PCE prediction stage, we used the deep learning architecture, which combines the deep feature extraction capability of residual networks and the advantage of a self-attention mechanism to capture long-range dependencies. In the result analysis stage, we performed an interpretable analysis of the key molecular descriptors by using a SHAP (SHapley Additive exPlanations) value.292.1. Data collection
In this study, we used the Harvard Organic Photovoltaics dataset (HOPV15) as the benchmark data.29 HOPV15 comprises detailed information on 350 small-molecule and polymer electron donors, along with their corresponding 6 acceptor materials (PC61BM, PC71BM, TiO2, C60, PDI, and ICB), making it one of the most comprehensive and diverse datasets available for organic photovoltaic performance analysis.30 A distinctive feature of HOPV15 is that it includes both experimental measurements extracted from the literature and theoretical predictions based on quantum chemical calculations and the Scharber model. The dataset reports key photovoltaic performance metrics, including open-circuit voltage (VOC), short-circuit current density (JSC), and power conversion efficiency (PCE), all estimated using the Scharber model.31 Additionally, the highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and the HOMO–LUMO gap of the donor materials were calculated using the B3LYP functional32,33 with the def2-SVP basis set.34 Although B3LYP tends to overestimate electron delocalization, it has been shown to reasonably reproduce HOMO–LUMO energy gaps in conjugated systems. Moreover, the associated computational errors are systematic, allowing for reliable trend analysis based on relative values.35 To ensure consistency with previous studies, calibration using experimental data further mitigates the influence of specific functional choices. By relying on a unified computational protocol, HOPV15 ensures internal consistency and avoids uncertainties that often arise from variations in experimental conditions.2.2. Data preprocessing
To ensure the generalization performance of the models, the dataset underwent meticulous preprocessing and validation. Initially, data cleansing involved removing three donor entries lacking acceptor information and three duplicates, resulting in a refined dataset of 344 unique donor–acceptor (D–A) pairs. Each pair comprised a complete molecular structure, experimentally determined power conversion efficiency (PCE), and quantum chemical electronic features. An analysis confirmed that the key performance indicators exhibited an approximately normal distribution, which is beneficial for predictive modeling.36 For robust model training and evaluation, the dataset was strategically split. The k-means clustering algorithm was employed to divide the data into an 80% training set and a 20% test set. The k-means clustering was performed with n_clusters = 5, initialization method “k-means++”, maximum iterations of 200, and random_state = 42 to ensure reproducibility. This clustering-based partitioning is critical for QSPR models, ensuring the test set resides within the model's applicability domain and maintaining a representative data. In each iteration, one fold served as the validation set, with the remaining nine forming the training set. This process was repeated 5 times, ensuring each fold was validated precisely once. The reported performance metrics represent the average and standard deviation across these 5 folds, providing a more robust assessment of the model's generalization capabilities than a single train-test split. While random partitioning was utilized, the inherent complexity and correlations within molecular datasets are acknowledged. Future work will explore advanced splitting methodologies, such as scaffold-based splitting, to further enhance the rigor of dataset partitioning.2.3. Molecular precoding
As shown in Fig. 1(a), for the encoding of acceptor molecules, we used a simple but effective 1-hot encoding scheme. This captures the essential differences between the receptors, most relevantly the receptor LUMO energy. The presence of a particular acceptor was denoted as 1 in its corresponding position, while all other positions were set to 0. This streamlined encoding approach effectively captured the fundamental differences between acceptor molecules, with particular emphasis on LUMO energy level variations that critically influence device performance. This precoding method combines computational simplicity with the ability to represent essential molecular characteristics relevant to photovoltaic applications. For the donor molecular characterization, as shown in Fig. 1(b), we employed the MolSig program to generate signature descriptors by analyzing atomic connectivity patterns with path lengths of 0–4 bonds.37 The program evaluated each atom's local chemical environment and bonding patterns, creating tree-like subgraphs that encode structural characteristics. After sorting and filtering descriptors based on statistical significance (removing those with fewer than two occurrences), we established a comprehensive feature pool of 695 descriptors that effectively capture the structural and electronic properties of our donor–acceptor materials. This approach ensured both computational efficiency and chemical interpretability essential for materials screening.2.4. Feature extraction
In this study, we used molecular descriptors to characterize the structural and physicochemical properties of both donor and acceptor materials. Given that an excessive number of descriptors can introduce noise, reduce model robustness, and lead to overfitting, we adopted a systematic feature selection strategy to identify the most relevant descriptors for predicting PCE. Ultimately, 625 molecular descriptors related to donor materials were selected, effectively capturing key molecular features influencing PCE while reducing the dimensionality of the feature space. This selection strategy not only improved computational efficiency but also enhanced model interpretability, which are critical for accurately predicting the performance of novel OPV materials.2.5. Model training and PCE prediction
In this study, the SolarPCE-Net introduced a residual network and the attention mechanism. As shown in Fig. 2, the deep feature extraction capabilities of residual networks, combined with the long-range dependency captured advantages of self-attention mechanisms, offering a novel approach to predicting materials performance.Compared with traditional networks, the core innovation lies in the synergistic design of the attention mechanism and residual structure: the attention module dynamically strengthens the key donor–acceptor interaction features, while the residual connection solves the gradient vanishing problem in the deep network through the “feature retention + incremental learning” mode, which enables the model to maintain accuracy and stability when dealing with high-dimensional molecular data.
| hn+1 = h1 + F(hn,W1) | (1) |
| F(h1) = W2 × ReLU(BN(W1×h1)) | (2) |
The batch normalization operation adopts the standard form:
 | (3) |
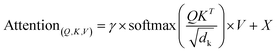 | (4) |
2.6. Assessment indicators
As shown in Fig. 1(d), to comprehensively assess the prediction performance of SolarPCE-Net, we use three assessment metrics including the coefficient of determination (R2), the mean absolute error (MAE), and the standard error (SE), as follows: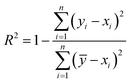 | (5) |
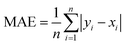 | (6) |
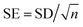 | (7) |
2.7. Model interpretation: characteristic contribution analysis based on SHAP values
As shown in Fig. 1(d), to further understand the prediction process and decision-making mechanism of SolarPCE-Net, we adopted SHAP values38 to perform model interpretation. The SHAP values derived from game theory38 are an important tool for measuring the contribution of individual features to the prediction and are particularly suitable for the interpretation of machine learning models.39 The SHAP value helps us understand the decision-making process of the model by quantifying the contribution of each feature to the prediction result. Assuming that the ith sample is mi and the jth feature of the ith sample is mij, the predicted value ni for the ith sample mi can be expressed as the baseline value nbase plus the sum of the SHAP values of all the features with the following formula: | (8) |
3. Results and discussion
3.1. Model hyperparameter configuration
In this study, we developed a residual neural network with the self-attention mechanism to predict PCE in OPVs. Multiple sets of experiments were conducted on the dimensionality of the hidden layers and the number of residual blocks in the architecture, and we found a combination of hyperparameters that performed consistently and predicted better, culminating in the use of 631-dimensional molecular descriptors as inputs, which were linearly projected into a 59-dimensional hidden space. Three consecutive residual blocks performed feature learning, each including a bilinear layer (maintaining 59D hidden dimensions), batch normalization, ReLU activation, and a self-attention module for capturing remote feature dependencies. In the attention mechanism, queries and keys were compressed to 15 dimensions (1/4 of the original dimension) while preserving full dimensionality (59D) for values. A learnable scaling parameter γ (initialized to zero) adaptively regulated the attention contribution. For the model training, we utilized an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 split (276 training samples vs. 68 test samples), empirically optimized for the dataset's high-dimensional sparsity (90.49% sparse features). The Adam optimizer was employed with an initial learning rate of 1 × 10−3 and batch size of 32 to balance gradient stability and computational efficiency. Training spanned 100 epochs using mean squared error (MSE) as the loss function. Batch normalization parameters (momentum = 0.9; epsilon = 1 × 10−5) were configured to mitigate internal covariate shift and accelerate convergence.
2 split (276 training samples vs. 68 test samples), empirically optimized for the dataset's high-dimensional sparsity (90.49% sparse features). The Adam optimizer was employed with an initial learning rate of 1 × 10−3 and batch size of 32 to balance gradient stability and computational efficiency. Training spanned 100 epochs using mean squared error (MSE) as the loss function. Batch normalization parameters (momentum = 0.9; epsilon = 1 × 10−5) were configured to mitigate internal covariate shift and accelerate convergence.
To address overfitting risks in the limited dataset size, multiple regularization strategies were integrated: batch normalization in residual blocks, skip connections for gradient propagation, attention dimension compression, and progressive attention modulation via the learnable γ parameter. The entire framework was implemented using PyTorch, with fixed random seeds to ensure reproducibility. All experiments were conducted on a NVIDIA GeForce RTX 3060 laptop GPU. The dataset was divided into a training set and a test set, with 80% of the training set and 20% of the test set. Each experiment was repeated independently 100 times to produce average results.
3.2. Comparisons
| Method | Train | Test | ||||
|---|---|---|---|---|---|---|
| R 2 | MAE | SE | R 2 | MAE | SE | |
| BRANNLP | 0.72 | 0.27 | 0.50 | 0.78 | 0.46 | 0.48 |
| MLP | 0.99 | 0.03 | 0.06 | 0.66 | 0.39 | 0.59 |
| RF | 0.93 | 0.18 | 0.29 | 0.76 | 0.37 | 0.51 |
| GBR | 0.92 | 0.23 | 0.30 | 0.71 | 0.39 | 0.54 |
| LR | 0.96 | 0.10 | 0.22 | −1.76 | 0.99 | 1.72 |
| MPNN | 0.97 | 0.14 | 0.16 | 0.70 | 0.38 | 0.55 |
| AttentiveFP | 0.98 | 0.10 | 0.14 | 0.67 | 0.37 | 0.59 |
| DMPNN | 0.98 | 0.12 | 0.14 | 0.77 | 0.34 | 0.50 |
| GAT | 0.84 | 0.28 | 0.42 | 0.60 | 0.42 | 0.64 |
| SolarPCE-Net | 0.90 | 0.24 | 0.35 | 0.81 | 0.35 | 0.45 |
The SolarPCE-Net demonstrates optimal balance between training performance and test generalization, avoiding the overfitting issues that plague other deep learning approaches. The tight correlation observed in its scatter plot, combined with the lowest test MAE and SE values, confirms its superior predictive reliability and establishes the SolarPCE-Net as the most suitable method for PCE prediction in organic photovoltaic materials.
Based on the results of 5-fold cross-validation using the full dataset descriptors, the SolarPCE-Net exhibited superior performance compared to other established machine learning and deep learning methods. As summarized in Fig. 4, the SolarPCE-Net achieved the highest average R2 score on the test set (0.6218 ± 0.1404) along with the lowest mean absolute error (MAE, 0.4362 ± 0.0772) and standard error (SE, 0.6480 ± 0.1867), indicating robust predictive accuracy and generalization capability. In contrast, traditional linear regression (LR) completely failed to model the task, yielding a strongly negative test R2 (−331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 ± 367
358 ± 367![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424) and abnormally high error values (MAE = 14
424) and abnormally high error values (MAE = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 812 ± 14
812 ± 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 046; SE = 46
046; SE = 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007 ± 41
007 ± 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344), clearly demonstrating its inadequacy for complex molecular descriptor relationships. Among ensemble methods, random forest (RF) and gradient boosting regression (GBR) displayed stable performance, with test R2 values of 0.5564 ± 0.0831 and 0.5031 ± 0.1092, respectively; however, their predictive accuracy still lagged behind that of the SolarPCE-Net. MLP achieved near-perfect results on training data (R2 = 0.9975 ± 0.0004), but performed poorly on the test set (R2 = 0.4342 ± 0.1689), reflecting pronounced overfitting. Other advanced graph neural network architectures, including MPNN (test R2 = 0.5433 ± 0.0845), AttentiveFP (0.5487 ± 0.1525), DMPNN (0.5573 ± 0.0831), and GAT (0.5585 ± 0.1029), achieved only moderate performance.
344), clearly demonstrating its inadequacy for complex molecular descriptor relationships. Among ensemble methods, random forest (RF) and gradient boosting regression (GBR) displayed stable performance, with test R2 values of 0.5564 ± 0.0831 and 0.5031 ± 0.1092, respectively; however, their predictive accuracy still lagged behind that of the SolarPCE-Net. MLP achieved near-perfect results on training data (R2 = 0.9975 ± 0.0004), but performed poorly on the test set (R2 = 0.4342 ± 0.1689), reflecting pronounced overfitting. Other advanced graph neural network architectures, including MPNN (test R2 = 0.5433 ± 0.0845), AttentiveFP (0.5487 ± 0.1525), DMPNN (0.5573 ± 0.0831), and GAT (0.5585 ± 0.1029), achieved only moderate performance.
Overall, these comparative results confirm that the SolarPCE-Net delivers not only leading predictive accuracy but also enhanced generalization in the context of PCE prediction based on comprehensive molecular descriptors, substantially outperforming both classical machine learning models and other state-of-the-art deep learning approaches.
The correlation between absolute prediction error and the corresponding uncertainty estimate provides a quantitative measure of how effectively uncertainty captures predictive reliability. As shown in Fig. 6, the SolarPCE-Net achieved a Pearson correlation coefficient of R = 0.418, exceeding most deep learning benchmarks such as MLP (R = 0.405), BRANNLP (R = 0.377), and MPNN (R = 0.295), but lower than some graph neural network variants including GAT (R = 0.455), DMPNN (R = 0.495), and AttentiveFP (R = 0.464), as well as the ensemble based random forest (R = 0.614). Gradient boosted regression (GBR) exhibited a weaker correlation (R = 0.326), while the linear regression baseline performed very poorly (R = −0.088), indicating its inability to establish a meaningful uncertainty–error relationship. Although SolarPCE-Net's Pearson R is moderate compared to certain ensemble models, this outcome reflects an intrinsic tradeoff between predictive accuracy and uncertainty–error coupling. Ensemble approaches such as RF often yield higher correlations because their predictive variance—largely driven by bootstrap sampling diversity—directly encodes epistemic uncertainty that scales with prediction difficulty. However, such models typically suffer from lower mean predictive accuracy and broader uncertainty ranges, leading to less precise confidence intervals. By contrast, SolarPCE-Net's self-attention enhanced residual architecture produces a more deterministic and smooth mapping from molecular descriptors to PCE, thereby reducing both the magnitude and variance of prediction errors. This “error compression” effect narrows the dynamic range of errors and uncertainties, which can attenuate the statistical correlation between them. From an applied perspective, this tradeoff is not detrimental. SolarPCE-Net's moderate correlation value still ensures that higher uncertainty predictions tend to coincide with larger errors while offering superior calibration and accuracy. The resulting balance between informative uncertainty estimates and predictive stability makes the SolarPCE-Net well-suited for risk-aware decision-making in high-throughput OPV material screening.
Calibration plots depict the agreement between predicted confidence and empirical accuracy, with the diagonal representing the ideal perfectly calibrated model. Curves to the left of the diagonal indicate under confidence, while curves to the right indicate overconfidence. As shown in Fig. 7, RF, MPNN, DMPNN, and GAT produce curves closest to the ideal line, crossing from the left to the right, suggesting balanced confidence behavior over the probability spectrum. SolarPCE-Net's curve lies on the right of the diagonal, exhibiting a mild tendency toward overconfidence; however, it remains closer to the ideal than MLP, GBR, LR, BRANNLP, and AttentiveFP, which deviate more substantially. This positioning indicates that SolarPCE-Net's uncertainty estimates, while slightly overconfident, are relatively well aligned with empirical accuracy, offering reliable confidence information for practical decision-making.
Representative samples with the highest uncertainty values further illustrate the practical utility of UQ, as shown in Table 2. High uncertainty predictions consistently correspond to broad 95% confidence intervals, reflecting reduced model confidence. For instance, sample 57 (true value = 3.2721) was predicted with a mean of 2.8765 and an uncertainty of 1.0170, resulting in a wide confidence interval ([0.8832, 4.8698]) that fully covered the ground truth. Similarly, sample 231 exhibited both high uncertainty (0.9529) and a relatively large error (1.1409), correctly signaling low reliability. Interestingly, not all high uncertainty cases correspond to poor predictions: sample 129 had a very small error (0.0989), yet was assigned high uncertainty (0.9632), reflecting the model's conservative recognition of regions in chemical space with limited training coverage. These examples show that SolarPCE-Net's uncertainty estimates act as meaningful indicators of prediction risk, either by flagging potentially erroneous predictions or by conservatively cautioning against overreliance when data support is limited.
| True value | Predicted mean | Uncertainty (std dev.) | 95% CI | Absolute error | |
|---|---|---|---|---|---|
| Sample 57 | 3.2721 | 2.8765 | 1.0170 | [0.8832, 4.8698] | 0.3956 |
| Sample 247 | 1.5025 | 2.0674 | 1.0021 | [0.1034, 4.0315] | 0.5650 |
| Sample 129 | 2.5847 | 2.6836 | 0.9632 | [0.7957, 4.5715] | 0.0989 |
| Sample 231 | 4.1499 | 3.0091 | 0.9529 | [1.1415, 4.8767] | 1.1409 |
| Sample 17 | 2.7344 | 2.7194 | 0.9101 | [0.9356, 4.5031] | 0.0150 |
Overall, the integrated UQ analysis highlights three key characteristics of SolarPCE-Net: it produces stable and compact uncertainty distributions that minimize extreme fluctuations in predictive confidence; it achieves moderate but informative error–uncertainty correlation, ensuring unreliable predictions are effectively flagged while maintaining high overall accuracy; and it delivers competitively calibrated outputs with only mild overconfidence, outperforming the majority of baselines. At the case level, high uncertainty predictions consistently correspond either to large errors or to unfamiliar chemical regions, providing valuable interpretability. Taken together, these findings establish the SolarPCE-Net as a model that not only achieves high predictive accuracy but also provides practically trustworthy uncertainty estimates. This balance of accuracy, stability, and reliable confidence makes the SolarPCE-Net particularly suitable for high-throughput virtual screening and guided experimental validation in the discovery of high performance organic photovoltaic materials.
3.3. Ablation study of SolarPCE-Net architecture on the HOPV15 dataset
| Train | Test | |||||
|---|---|---|---|---|---|---|
| R 2 | MAE | SE | R 2 | MAE | SE | |
| SolarPCE-Net | 0.90 | 0.24 | 0.35 | 0.81 | 0.35 | 0.45 |
| w/o Self-attention | 0.93 | 0.21 | 0.28 | 0.54 | 0.52 | 0.70 |
| w/o Residual connections | −1.51 | 1.37 | 1.72 | −2.07 | 1.52 | 1.81 |
| w/o Full dim in attention | 0.93 | 0.21 | 0.29 | 0.50 | 0.50 | 0.73 |
3.3.1.1 Self-attention mechanism analysis. Removing the self-attention modules, which were replaced with standard feed-forward layers, resulted in a significant decrease in performance. The test R2 fell from 0.81 to 0.54, with MAE increasing from 0.35 to 0.52. This highlights the essential role of self-attention in capturing long-range dependencies and effectively weighting molecular substructures and chemical patterns, crucial for modeling donor–acceptor interactions.
3.3.1.2 Residual connection analysis. Without residual connections, the network exhibited a sharp performance drop, with a test R2 of −2.07 and an MAE of 1.52. These connections are vital for enabling stable gradient propagation through deep layers, which ensures robust training and generalization, especially for molecular data characterized by high dimensionality and limited size.
3.3.1.3 Attention dimension analysis. The SolarPCE-Net employs a strategic dimensionality reduction approach, compressing queries and keys to one-fourth of the original dimension while preserving full dimensionality for values. This design achieved a test R2 of 0.81, significantly outperforming the full-dimension variant which only reached 0.50. The selective reduction strategy effectively balances computational efficiency with information preservation, demonstrating that complete molecular information in value vectors is essential for accurate PCE prediction.
| Encoding scheme (donor + acceptors) | Train | Test | ||||
|---|---|---|---|---|---|---|
| R 2 | MAE | R 2 | MAE | R 2 | MAE | |
| 6 + 625 | 0.90 | 0.24 | 0.35 | 0.81 | 0.35 | 0.45 |
| 6 + 6 | 0.95 | 0.18 | 0.24 | 0.30 | 0.62 | 0.87 |
| 625 + 625 | 0.99 | 0.09 | 0.11 | 0.63 | 0.39 | 0.63 |
| 625 | 0.91 | 0.23 | 0.33 | 0.79 | 0.38 | 0.48 |
3.3.2.1 Minimal symmetric encoding (6 + 6). Utilizing only 6 features for donors and acceptors led to poor generalization, with a test R2 of 0.30, despite achieving a training R2 of 0.95. This underscored severe underfitting given the complex donor–acceptor relationships in OPV materials.
3.3.2.2 High-dimensional symmetric encoding (625 + 625). While this symmetric approach achieved excellent training results with an R2 of 0.99, it was prone to overfitting, yielding a test R2 of 0.63. The limited diversity of acceptors could not justify such high-dimensional representations.
3.3.2.3 Donor-only encoding (625). Using donor descriptors alone, the model performed competitively with a test R2 of 0.79, suggesting that donor characteristics predominantly influence PCE in the dataset. This aligns with the notion that simplified acceptor representations should suffice due to their standardized properties.
3.3.2.4 Chemical justification for asymmetric encoding. The choice of asymmetric encoding reflects the chemical reality of OPV systems, with standardized acceptors primarily distinguished by their LUMO levels, while donors require detailed descriptors given their structural diversity.
These results indicate that domain knowledge should guide feature encoding design. The asymmetric encoding used in the SolarPCE-Net not only improves predictive performance but also ensures chemical interpretability, providing a principled basis for future modeling strategies in materials science.
3.4. SolarPCE-Net performance analysis based on donor molecular descriptors
The original dataset contains donor–acceptor molecular descriptors. Through the preliminary experimental validation, the proposed model shows good performance in handling these descriptors, outperforming other methods. To further explore the PCE prediction performance of our SolarPCE-Net using donor molecular data, we conducted experiments using donor molecular descriptors alone as a new dataset, with results shown in Table 5 and Fig. 8. The experimental results demonstrate that the SolarPCE-Net achieved the highest R2 value (0.79) on the test set while maintaining the lowest error metrics, including MAE (0.38) and SE (0.48). This performance validates the model's superior predictive capability and outstanding generalization performance when handling complex molecular descriptor data. In contrast, other methods exhibited certain limitations. For instance, while Random Forest (RF) and Gradient Boosting Regression (GBR) achieved R2 values of 0.76 and 0.75, respectively, on the test set, with comparable MAE (0.36) and SE (0.51), their predictive performance still fell slightly short of the SolarPCE-Net. Message Passing Neural Network (MPNN) demonstrated good stability on the test set (R2 = 0.72, MAE = 0.34, and SE = 0.54) but failed to further enhance prediction accuracy. Furthermore, the Attention Fingerprint model (AttentiveFP) and Deep Message Passing Neural Network (DMPNN) performed poorly on the test set, with AttentiveFP achieving an R2 of only 0.61 and DMPNN an even lower R2 of 0.34. Both results indicate that these methods struggle to capture the complexity of donor molecular descriptors. Notably, linear regression (LR) exhibited exceptionally poor test performance, with an R2 value of −2.24 and extremely high error (MAE = 4417 and SE = 1547), indicating its complete inability to adapt to this complex dataset. In contrast, the Multi-Layer Perceptron (MLP) performed excellently on the training set (R2 = 0.99) but showed a significant decline on the test set (R2 = 0.66, MAE = 0.39, and SE = 0.60), revealing pronounced overfitting issues.| Method | Train | Test | ||||
|---|---|---|---|---|---|---|
| R 2 | MAE | SE | R 2 | MAE | SE | |
| BRANNLP | 0.89 | 0.24 | 0.35 | 0.72 | 0.41 | 0.54 |
| MLP | 0.99 | 0.03 | 0.06 | 0.66 | 0.39 | 0.60 |
| RF | 0.92 | 0.19 | 0.30 | 0.76 | 0.36 | 0.51 |
| GBR | 0.93 | 0.22 | 0.29 | 0.75 | 0.36 | 0.51 |
| LR | 0.92 | 0.18 | 0.30 | −2.24 | 4417 | 1547 |
| MPNN | 0.97 | 0.10 | 0.19 | 0.72 | 0.34 | 0.54 |
| AttentiveFP | 0.97 | 0.12 | 0.16 | 0.61 | 0.40 | 0.62 |
| DMPNN | 0.74 | 0.37 | 0.52 | 0.34 | 0.66 | 0.99 |
| GAT | 0.78 | 0.30 | 0.49 | 0.43 | 0.43 | 0.77 |
| SolarPCE-Net | 0.91 | 0.23 | 0.33 | 0.79 | 0.38 | 0.48 |
To further evaluate the performance of models based on donor molecular descriptors, we employed five-fold cross-validation to comprehensively assess the generalization capabilities of each method and compared the SolarPCE-Net against other mainstream approaches. As shown in Fig. 9, in the five-fold cross-validation based on donor molecular descriptors, the SolarPCE-Net achieved the highest average R2 value (0.6290 ± 0.1128) on the test set, while its MAE (0.4322 ± 0.0778) and SE (0.6438 ± 0.1529) remained within the lowest range, demonstrating superior generalization capability. In contrast, traditional regression models like linear regression (R2 = −546,435 ± 797,448) completely failed, while random forest (R2 = 0.5528 ± 0.0879) and gradient boosting regression (R2 = 0.5116 ± 0.1066) delivered stable yet limited prediction accuracy. Among deep learning approaches, the Multi-Layer Perceptron (MLP) exhibited poor test performance due to overfitting (R2 = 0.3139 ± 0.1664). AttentionFP (R2 = 0.5610 ± 0.1482) performed better but still fell short of the SolarPCE-Net, while graph-based methods MPNN, DMPNN, and GAT showed generally mediocre performance (R2 = 0.3888 ± 0.2378, 0.4282 ± 0.1721, and 0.3888 ± 0.2378, respectively). Overall, the SolarPCE-Net demonstrated significant advantages in handling complex molecular descriptors and predicting photoelectric conversion efficiency, outperforming other traditional and deep learning models.
 | ||
| Fig. 9 Performance comparison of methods on donor molecular descriptors in the HOPV15 dataset using 5-fold cross-validation. | ||
In summary, our SolarPCE-Net uniquely achieves reliable PCE prediction using donor-only molecular descriptors, overcoming the limitations of conventional models, demonstrating its robustness. Its adaptability in donor-centric modeling stems from attention-guided feature abstraction and adaptive regularization, which effectively distill critical donor-specific patterns from high-dimensional sparse data while suppressing descriptor redundancy.
3.5. Model interpretation analysis for screening donor molecular descriptors
In this study, we employed a self-attention mechanism to screen donor molecular descriptors. To evaluate feature importance, we utilized both attention weights and SHAP values. The self-attention mechanism dynamically adjusts feature importance, thereby enhancing the model's flexibility and efficiency in handling complex data. In Table 6, we present the relationship between molecular descriptors and their corresponding molecular structures, where these identified structural features play a crucial role in understanding molecular properties and functions. We make new coding names for each donor molecular descriptor in SI 1. | ||
| Fig. 10 Top-20 molecular descriptors ranked by the attention weights. (a) Overall molecular descriptors. (b) Donor molecular descriptors. | ||
MD3, characterized by a sulfur-containing five-membered ring, enhances electron-donating capabilities, which significantly improves the charge transport efficiency.39 This structural feature is essential for achieving device stability and efficiency, making it a promising component in high-performance OPV materials. MD6, with its carbon–carbon double bonds and sulfur atoms, forms an enhanced conjugated system that facilitates electron delocalization, thereby improving charge mobility.40 The optimization of this conjugated connection is crucial for achieving high PCE, highlighting its potential as a key structural motif in future OPV designs. MD12, a linear conjugated structure, supports intramolecular electron delocalization, which enhances charge transport.41 As a fundamental unit in efficient photovoltaic materials, optimizing the conjugation length and arrangement of MD12 is vital for maximizing device performance. MD53, featuring a complex conjugated structure with both oxygen and sulfur, optimizes energy level alignment and improves charge separation efficiency.42 This combination is critical for high-efficiency energy conversion, positioning MD53 as a valuable structural element in the design of next-generation OPV materials. These molecular descriptors collectively underscore the importance of strategic structural optimization in the development of OPV materials with superior PCE.43
In summary, this feature selection of our method not only enhances the model performance but also provides an interpretable insight into the decision-making process. These molecular descriptors MD6, MD53, MD12 and MD3, as substructures, play a significant role in the development of high-performance OPV materials. Their unique structural characteristics contribute to improved charge transport, energy level alignment, and device stability. By strategically incorporating these substructures, future research can focus on optimizing donor–acceptor interactions and enhancing the overall photovoltaic efficiency. This approach holds promise for achieving breakthroughs in organic photovoltaic technology, potentially leading to more efficient and cost-effective solar energy solutions.
In Fig. 12(a and c), we present the feature importance and SHAP values of these selected features in the GBR model, while Fig. 12(b and d) show the corresponding results in the RF model. In Fig. 12, the key molecular descriptors (MD45, MD12, and MD3) are prominently highlighted both in the attention analysis, which pinpoints focus areas in the feature space, and in the SHAP value evaluation, which quantifies their contributions. By integrating the attention mechanism—which helps identify areas of the feature space that merit further exploration—with SHAP value analysis, we obtained a more comprehensive understanding of the critical molecular descriptors in OPV materials and support the concept of utilizing attention-driven feature pre-screening. Moreover, by synergistically combining the focus-oriented insights from the attention mechanism with the quantitative explanations derived from SHAP, we reveal the roles of these critical descriptors. This dual-validation consensus not only validates the attention mechanism's capability to identify physically meaningful features but also establishes a robust foundation for descriptor prioritization in OPV material design. Crucially, this dual-validation framework confirms the reliability of attention weights as a standalone feature pre-screening tool, effectively bridging data-driven modeling with domain-specific physicochemical insights.
3.6. Application analysis of screened D–A pairs using the SolarPCE-Net
To apply our SolarPCE-Net method to the practical screening task, we randomly combined donor and recipient pairs in the HOPV15 dataset. The corresponding data are recorded in SI 2. By leveraging the advanced capabilities of SolarPCE-Net, we applied the SolarPCE-Net to predict the PCE value of unexplored D–A combination. All PCE prediction results with randomly combined D–A pairs are recorded in SI 3. Our method screened numerous D–A combinations and identified potential D–A pairs that exhibit high accuracy and high PCE. We applied two screening strategies to the HOPV15 dataset: (i) the predicted filling efficiency (PCE) must exceed 4.5 (higher predicted PCE threshold, 75% of the highest predicted PCE value 5.96) to ensure only high-performance organic photovoltaic candidate materials are included; (ii) predicted uncertainty (standard deviation) must not exceed 0.30 to guarantee high prediction confidence. Under these constraints, six donor–acceptor pairs were successfully identified from the dataset, as shown in Table 7.| No. | Donors | Acceptors | Predicted_PCE | Uncertainty_Std |
|---|---|---|---|---|
| 1 | Cn1c2ccccc2c2ccc(–c3ccc(–c4nnc(–c5cccs5)c5nonc54)s3)cc21 | C60 | 4.670158 | 0.2972964 |
| 2 | Cn1c2cc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C#N)C#N)sc2c2sc(C C(C#N)C#N)sc2c2sc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C#N)C#N)cc21 C(C#N)C#N)cc21 |
ICB | 4.639657 | 0.2777083 |
| 3 | N#CC(C#N)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C#N)C#N)s4)cc3)cc2)s1 C(C#N)C#N)s4)cc3)cc2)s1 |
PDI | 4.627146 | 0.2776075 |
| 4 | N#CC(C#N)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C#N)C#N)s4)cc3)cc2)s1 C(C#N)C#N)s4)cc3)cc2)s1 |
TiO2 | 4.598744 | 0.2698893 |
| 5 | N#CC(C#N)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C#N)C#N)s4)cc3)cc2)s1 C(C#N)C#N)s4)cc3)cc2)s1 |
ICB | 4.584405 | 0.2566765 |
| 6 | N#CC(C#N)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C Cc1ccc(–c2ccc(N(c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C Cc5cccs5)s4)cc3)c3ccc(–c4ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C#N)C#N)s4)cc3)cc2)s1 C(C#N)C#N)s4)cc3)cc2)s1 |
C60 | 4.544224 | 0.2635908 |
The three shortlisted donor molecules share several key structural motifs that underpin their predicted high performance and low uncertainty. All feature an extended π-conjugated backbone, frequently incorporating fused aromatic or heteroaromatic units that enforce molecular planarity and rigidity, thereby enhancing π–π stacking propensity and facilitating efficient charge transport in the solid state. Each donor exhibits a pronounced donor–acceptor (D–A) push–pull architecture: electron-rich fragments such as thiophene or polycyclic aromatic systems serve as donor segments, while strong electron withdrawing units—such as dicyanovinyl groups, fused nitrogen containing heterocycles, or diazine moieties—are positioned at the molecular termini. This configuration promotes intramolecular charge transfer (ICT), broadens and redshifts absorption spectra, and fine-tunes the frontier orbital energies to achieve a favorable HOMO/LUMO alignment. The rigid and coplanar π-frameworks further improve molecular packing and hole mobility, while terminal acceptor moieties lower the LUMO levels, providing an energetic driving force for exciton dissociation. These intrinsic donor properties are complemented by favorable interactions with multiple classes of electron acceptors. With planar small molecule acceptors such as perylene diimide (PDI), the donors' coplanar backbones enable strong face on π–π stacking, reducing exciton diffusion lengths before dissociation. Against spherical fullerene derivatives (C60, ICB), the donors' rigid conjugated frameworks promote intimate interfacial contact and isotropic electronic coupling, ensuring rapid electron transfer and balanced transport. For inorganic TiO2, the significant dipole moments arising from the D–A push–pull design can strengthen interfacial electric fields, facilitating charge separation and suppressing recombination. The recurrence of these donor cores in top-ranked, low-uncertainty predictions across diverse acceptor chemistries underscores their structural compatibility and energetic versatility, making them chemically plausible and experimentally promising candidates for high performance organic photovoltaic devices.
In summary, these characteristics collectively position the selected D–A pairs as promising candidates to enhance device performance. Future work could test these predictions through laboratory work or high-fidelity simulations. Our SolarPCE-Net not only identified high-performance OPV materials but also provided a strategic framework to accelerate the discovery of efficient solar energy solutions.
4. Conclusion
In this study, we proposed the SolarPCE-Net, a deep learning-based framework for predicting the power conversion efficiency (PCE) of organic photovoltaic (OPV) materials. By combining residual network architectures with a self-attention mechanism, the model achieved excellent performance on the HOPV15 dataset, reaching an R2 of 0.81 on the independent test set—significantly outperforming existing machine learning methods. Even when using only donor molecular descriptors, the SolarPCE-Net maintained an R2 of 0.79, validating the effectiveness of its architectural design. Five-fold cross-validation yielded an average R2 of 0.62 with relatively low variance across folds, indicating that while performance decreases under the more stringent data partitioning—which better simulates extrapolation to unseen chemotypes—the model still retains reasonable generalization capability, given the limited dataset size. The feature processing strategy integrates molecular signature descriptors generated by MolSig with quantum chemical calculation features, providing rich structural and electronic information. This multimodal fusion not only improves predictive accuracy but also enhances generalizability. Through SHAP value analysis and attention weight visualization, we identified key molecular descriptors influencing PCE and revealed interpretable structure–property relationships, enhancing the credibility of predictions. Uncertainty quantification (UQ) analysis confirmed that the model can effectively separate high-confidence from low-confidence predictions, enabling reliable prioritization of candidates in high-throughput virtual screening. Applying a dual-threshold filter (PCE > X, UQ ≤ Y) to new donor–acceptor pairs yielded a compact set of synthetically feasible, high-performance candidates across diverse acceptor classes, demonstrating the method's practical potential to accelerate OPV material discovery.Nevertheless, limitations remain: the model does not explicitly account for device processing parameters (e.g., film thickness, solvent, and annealing), relies on a relatively small and chemically imbalanced dataset compared to the vast OPV chemical space, and omits morphological descriptors such as packing, miscibility, or crystallinity that strongly influence device performance. Future work will focus on (i) integrating process- and morphology-related features, (ii) expanding datasets via high-throughput computation and experimental data sharing, and (iii) developing multimodal learning architectures to jointly model molecular, morphological, and processing information. Overall, the SolarPCE-Net delivers accurate, interpretable, uncertainty-aware PCE predictions with demonstrated generalization ability under cross-validation, highlighting its promise for guiding rational OPV material design and bridging the gap between molecular discovery and device optimization.
Author contributions
Xingyu Liu: investigation, validation, visualization, writing – original draft. Bo Hu: data curation, formal analysis, resources, writing – original draft. Pei Liu: formal analysis, methodology, resources, software. Meng Huang: conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing. Ming Li: funding acquisition, software, supervision. Yuwei Wan: investigation, resources, validation. Bram Hoex: project administration, writing – review & editing. Tong Xie: data curation, investigation, resources, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
The source code used to replicate all our analyses, including all real data, is available at the following link: https://github.com/Liupei-Luna/pcenet.git.Supplementary information: SI 1 is the code names of acceptors and donor molecular descriptors. SI 2 is feature extraction results of acceptors and donor moleculars. SI 3 is the predicted PCE results with new D–A pairs. See DOI: https://doi.org/10.1039/d5ta04854k.
Acknowledgements
This work was partially supported by the National Natural Science Foundation of China (Grant 12401679), the Teaching Reform Research Project for Jiangsu Province Academic Degrees and Graduate Education of China (Grant JGKT25_B053), the Graduate Research and Practice Innovation Program of Jiangsu Province SJCX25_2117, the Jiangsu Provincial Higher Education Basic Science (Natural Science) Research Project (Grant 25KJD520001), and the Haiyan Project (Grant KK25015) funded by the Lianyungang government, China.References
- P. G. V. Sampaio and M. O. A. González, A review on organic photovoltaic cell, Int. J. Energy Res., 2022, 46(13), 17813–17828 CrossRef.
- M. Raïssi, S. Wageh and A. A. Al-Ghamdi, et al., Towards large area production, stretchability, flexibility, and stability of efficient printed organic tandem solar cells, J. Mater. Chem. A, 2023, 11(46), 25578–25594 RSC.
- S. Park, T. Kim and S. Yoon, et al., Progress in Materials, Solution Processes, and Long-Term Stability for Large-Area Organic Photovoltaics, Adv. Mater., 2020, 32(51), 2002217 CrossRef CAS PubMed.
- A. Machín and F. Márquez, Advancements in photovoltaic cell materials, Silicon, Organic, and Perovskite Solar cells, Materials, 2024, 17(5), 1165 CrossRef PubMed.
- M. Moser, A. Wadsworth and N. Gasparini, et al., Challenges to the success of commercial organic photovoltaic products, Adv. Energy Mater., 2021, 11(18), 2100056 CrossRef CAS.
- W. Cao and J. Xue, Recent progress in organic photovoltaics, device architecture and optical design, Energy Environ. Sci., 2014, 7(7), 2123–2144 RSC.
- L. Sun, K. Fukuda and T. Someya, Recent progress in solution-processed flexible organic photovoltaics, npj Flexible Electron., 2022, 6(1), 89 CrossRef.
- A. Wadsworth, M. Moser and A. Marks, et al., Critical review of the molecular design progress in non-fullerene electron acceptors towards commercially viable organic solar cells, Chem. Soc. Rev., 2019, 48(6), 1596–1625 RSC.
- A. Zhugayevych and S. Tretiak, Theoretical description of structural and electronic properties of organic photovoltaic materials, Annu. Rev. Phys. Chem., 2015, 66(1), 305–330 CrossRef CAS PubMed.
- E. R. Rwenyagila, A review of organic photovoltaic energy source and its technological designs, Int. J. Photoenergy, 2017, 2017(1), 1656512 Search PubMed.
- I. Y. Kanal, S. G. Owens and J. S. Bechtel, et al., Efficient computational screening of organic polymer photovoltaics, J. Phys. Chem. Lett., 2013, 4(10), 1613–1623 CrossRef CAS.
- M. C. Scharber, D. Mühlbacher and M. Koppe, et al., Design rules for donors in bulk-heterojunction solar cells—Towards 10% energy-conversion efficiency, Adv. Mater., 2006, 18(6), 789–794 CrossRef CAS.
- G. H. Kim, C. Lee and K. Kim, et al., Novel structural feature-descriptor platform for machine learning to accelerate the development of organic photovoltaics, Nano Energy, 2023, 106, 108108 CrossRef CAS.
- Y. Liu, T. Zhao and W. Ju, et al., Materials discovery and design using machine learning, J. Mater., 2017, 3(3), 159–177 Search PubMed.
- S. Nagasawa, E. Al-Naamani and A. Saeki, Computer-aided screening of conjugated polymers for organic solar cell, classification by random forest, J. Phys. Chem. Lett., 2018, 9(10), 2639–2646 CrossRef CAS.
- P. B. Jørgensen, M. Mesta, S. Shil, J. M. García Lastra, K. W. Jacobsen and K. S. Thygesen, et al., Machine learning-based screening of complex molecules for polymer solar cells, J. Chem. Phys., 2018, 148(24), 241735 CrossRef PubMed.
- W. Sun, Y. Zheng and K. Yang, et al., Machine learning–assisted molecular design and efficiency prediction for high-performance organic photovoltaic materials, Sci. Adv., 2019, 5(11), eaay4275 CrossRef CAS PubMed.
- H. Sahu, W. Rao and A. Troisi, et al., Toward predicting efficiency of organic solar cells via machine learning and improved descriptors, Adv. Energy Mater., 2018, 8(24), 1801032 CrossRef.
- R. J. Richards and A. Paul, An attention-driven long short-term memory network for high throughput virtual screening of organic photovoltaic candidate molecules, Sol. Energy, 2021, 224, 43–50 CrossRef CAS.
- K. Chen, D. Zhang and L. Yao, et al., Deep learning for sensor-based human activity recognition, Overview, challenges, and opportunities, ACM Comput. Surv., 2021, 54(4), 1–40 Search PubMed.
- X. Tong, Y. Wan, Y. Zhou, W. Huang, Y. Liu, Q. Linghu, S. Wang, C. Kit, C. Grazian, W. Zhang and B. Hoex, Creation of a structured solar cell material dataset and performance prediction using large language models, Patterns, 2024, 5(5), 100955 CrossRef PubMed.
- F. Häse, L. M. Roch and P. Friederich, et al., Designing and understanding light-harvesting devices with machine learning, Nat. Commun., 2020, 11(1), 4587 CrossRef PubMed.
- S. Kar, Applications of Predictive Modeling for Dye-Sensitized Solar Cells (DSSCs), Materials Informatics II, Software Tools and Databases, 2025, pp. 167–198 Search PubMed.
- T. F. G. G. Cova and A. A. C. C. Pais, Deep learning for deep chemistry, optimizing the prediction of chemical patterns, Front. Chem., 2019, 7, 809 CrossRef CAS PubMed.
- Y. Ding, B. Qiang and Q. Chen, et al., Exploring chemical reaction space with machine learning models, Representation and feature perspective, J. Chem. Inf. Model., 2024, 64(8), 2955–2970 CrossRef CAS.
- S. A. Lopez, et al., The Harvard organic photovoltaic dataset, Sci. Data, 2016, 3(1), 1–7 Search PubMed.
- N. Meftahi, M. Klymenko and A. J. Christofferson, et al., Machine learning property prediction for organic photovoltaic devices, npj Comput. Mater., 2020, 6, 166 CrossRef CAS.
- M. A. Yirik and C. Steinbeck, Chemical graph generators, PLoS Comput. Biol., 2021, 17(1), e1008504 CrossRef CAS.
- Q. Zhao, Y. Shan and C. Xiang, et al., Predicting power conversion efficiency of binary organic solar cells based on Y6 acceptor by machine learning, J. Energy Chem., 2023, 82, 139–147 CrossRef.
- M. C. Scharber, et al., Design rules for donors in bulk-heterojunction solar cells—towards 10% energy-conversion efficiency, Adv. Mater., 2006, 18(6), 789–794 CrossRef CAS.
- H. Sahu, et al., Toward predicting efficiency of organic solar cells via machine learning and improved descriptors, Adv. Energy Mater., 2018, 8(24), 1801032 CrossRef.
- A. Becke, Density-functional thermochemistry, the role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652 CrossRef CAS.
- J. Tirado-Rives and W. L. Jorgensen, Performance of B3LYP density functional methods for a large set of organic molecules, J. Chem. Theory Comput., 2008, 4(2), 297–306 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn, design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(15), 3297–3305 RSC.
- J. Ma, S. Li and Y. Jiang, A time-dependent DFT study on band gaps and effective conjugation lengths of polyacetylene, polyphenylene, polypentafulvene, poly-cyclopentadiene, polypyrrole, polyfuran, polysilole, polyphosphole, and poly-thiophene, Macromolecules, 2002, 35(4), 1109–1115 CrossRef CAS.
- A. R. Katritzky, et al., Quantitative correlation of physical and chemical properties with chemical structure, utility for prediction, Chem. Rev., 2010, 110(12), 5714–5789 CrossRef CAS.
- P. Carbonell, L. Carlsson and J. L. Faulon, Stereo signature molecular descriptor, J. Chem. Inf. Model., 2013, 53(4), 887–897 CrossRef CAS PubMed.
- S. Lipovetsky, Game theory in regression modeling, A brief review on Shapley value regression, Model Assisted Statistics Appl., 2021, 16(2), 165–168 Search PubMed.
- I. E. Kumar, S. Venkatasubramanian, C. Scheidegger, et al., Problems with Shapley-value-based explanations as feature importance measures, in International Conference on Machine Learning, PMLR, 2020, pp. 5491–5500 Search PubMed.
- V. Piradi, F. Yan, X. Zhu and W. Y. Wong, A recent overview of porphyrin-based π-extended small molecules as donors and acceptors for high-performance organic solar cells, Mater. Chem. Front., 2021, 5, 7119–7133 RSC.
- A. J. Heeger, Semiconducting Polymers, the Third Generation, Chem. Soc. Rev., 2010, 39(9), 2354–2371 RSC.
- K. I. Moineau-Chane Ching, Impact of Alkyl-Based Side Chains in Conjugated Materials for Bulk Heterojunction Organic Photovoltaic Cells—A Review, Energies, 2023, 16, 6639 CrossRef CAS.
- D. Garratt, L. Misiekis and D. Wood, et al., Direct observation of ultrafast exciton localization in an organic semiconductor with soft X-ray transient absorption spectroscopy, Nat. Commun., 2022, 13, 3414 CrossRef CAS PubMed.
- X. Du, L. Lüer and T. Heumueller, et al., Elucidating the full potential of OPV materials utilizing a high-throughput robot-based platform and machine learning, Joule, 2021, 5(2), 495–506 CrossRef CAS.
- Y. Chen, P. Long and B. Liu, et al., Development and application of Few-shot learning methods in materials science under data scarcity, J. Mater. Chem. A, 2024, 12(44), 30249–30268 RSC.
- H. Huang, H. Huang and Z. Zheng, et al., Insights into infrared crystal phase characteristics based on deep learning holography with attention residual network, J. Mater. Chem. A, 2025, 13(8), 6009–6019 RSC.
- A. Eibeck, D. Nurkowski and A. Menon, et al., Predicting power conversion efficiency of organic photovoltaics: models and data analysis, ACS Omega, 2021, 6(37), 23764–23775 CrossRef CAS.
- J. Qiu, H. H. Lam, X. Hu, et al., Accelerating High-Efficiency Organic Photovoltaic Discovery via Pretrained Graph Neural Networks and Generative Reinforcement Learning, AI for Accelerated Materials Design-ICLR, 2025 Search PubMed.
- N. T. Hung, R. Okabe and A. Chotrattanapituk, et al., Universal Ensemble-Embedding Graph Neural Network for Direct Prediction of Optical Spectra from Crystal Structures, Adv. Mater., 2024, 36(46), 2409175 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |