Bismuth ferrite (Bi2Fe4O9) nanosheets: an efficient adsorbent for triclosan
Received
4th August 2025
, Accepted 15th November 2025
First published on 17th November 2025
Abstract
Triclosan (TCS) is the most common antimicrobial agent used in personal care products. Even a small concentration of TCS (<0.3 mg L−1) in water poses a potential threat to human and aquatic lives. We investigated TCS adsorption from aqueous solutions using hydrothermally synthesized bismuth ferrite (Bi2Fe4O9) or BFO materials. Different compositional variations of bismuth ferrite were obtained by altering the mole ratio of bismuth and iron precursors (Bi/Fe ratio) and NaOH concentration. The synthesized BFO materials were then analyzed using XRD, FESEM, BET, FTIR spectroscopy and zeta potential analysis. Moreover, batch adsorption experiments were conducted to investigate the influence of different BFO materials, pH and adsorbent loading on the TCS adsorption equilibrium. We examined the efficacy of TCS adsorption by different BFO materials and fitted the experimental data to different isotherms. The Redlich–Peterson model was the most suitable for describing the TCS adsorption on BFO. Furthermore, the mean free adsorption energy obtained from the D-R isotherm indicated that physical adsorption played a key role in the adsorption process. The adsorption kinetic fitting revealed that TCS adsorption followed a pseudo-second-order kinetic model. Our experimental results showed that altering the solution pH drastically affected the adsorption behaviour. The interaction mechanism revealed a high TCS adsorption rate attributed to hydrogen bonding and electrostatic interactions. The BFO sample with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi/Fe mole ratio and 5 M NaOH concentration demonstrated the maximum TCS adsorption capacity, reaching 903 mg g−1 at pH 3, with a 0.2 g L−1 adsorbent loading at 298 K. This remarkable adsorption capacity of BFO nanosheets with minimal adsorbent loading and material stability validates its strong potential as a sustainable adsorbent for the efficient removal of emerging contaminants, like TCS, from wastewater.
1 Bi/Fe mole ratio and 5 M NaOH concentration demonstrated the maximum TCS adsorption capacity, reaching 903 mg g−1 at pH 3, with a 0.2 g L−1 adsorbent loading at 298 K. This remarkable adsorption capacity of BFO nanosheets with minimal adsorbent loading and material stability validates its strong potential as a sustainable adsorbent for the efficient removal of emerging contaminants, like TCS, from wastewater.
Sustainability spotlight
Bismuth ferrite (Bi2Fe4O9 or BFO) has recently emerged as a potential adsorbent. It is composed of bismuth and iron elements, with relatively low toxicity, good environmental compatibility and minimal leaching risk, making it an emerging material in environmental remediation. The application of BFO as an adsorbent for the removal of pollutants found in personal care products, e.g. triclosan (TCS), is not reported yet. TCS is a persistent antimicrobial agent found in personal care products. Its extensive use has led to environmental contamination, particularly in water bodies, with potential risks of antibiotic resistance, endocrine disruption, and toxicity to aquatic life. The BFO nanosheets synthesized using a Bi/Fe mole ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5 M NaOH exhibited a TCS adsorption capacity of 903 mg g−1 in 180 minutes at pH 3 and an adsorbent loading of 0.2 g L−1, which is quite higher than that reported in the literature (average TCS adsorption capacity ∼190 mg g−1). This rapid adsorption of TCS onto BFO occurs due to hydrogen bonding and electrostatic interactions. It offers an environmentally friendly solution that reduces the reliance on toxic chemicals or energy-intensive processes. Moreover, it can be easily regenerated and reused, enhancing its sustainability profile. By integrating BFO into wastewater treatment systems, we can take a step toward cleaner water and a greener future. 1 and 5 M NaOH exhibited a TCS adsorption capacity of 903 mg g−1 in 180 minutes at pH 3 and an adsorbent loading of 0.2 g L−1, which is quite higher than that reported in the literature (average TCS adsorption capacity ∼190 mg g−1). This rapid adsorption of TCS onto BFO occurs due to hydrogen bonding and electrostatic interactions. It offers an environmentally friendly solution that reduces the reliance on toxic chemicals or energy-intensive processes. Moreover, it can be easily regenerated and reused, enhancing its sustainability profile. By integrating BFO into wastewater treatment systems, we can take a step toward cleaner water and a greener future.
|
1. Introduction
Triclosan [5-chloro-2-(2, 4-dichloro-phenoxyphenol)] (TCS) is a common antimicrobial agent found in many personal care products like soaps, toothpaste, and cosmetics.1,2 The high prevalence of TCS in consumer products contributes significantly to its presence in wastewater. Once these products are used and washed off, TCS enters the sewage system through household drains, contributing to the influent stream of wastewater treatment plants. Li et al. have reported the wastewater influent and effluent concentrations of TCS to be 86000 ng L−1 and 5400 ng L−1, respectively, and demonstrated a significant decrease in TCS concentrations from the influent to the effluent stream of wastewater treatment plants.2 The globally reported concentrations of TCS in water are as follows: 1.4 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ng L−1 in surface waters, 20 to 86
000 ng L−1 in surface waters, 20 to 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 ng L−1 in wastewater influent, 23 to 5370 ng L−1 in wastewater effluent, and less than 0.001 to 100 ng L−1 in seawater.3 However, the persistence of the measurable amounts of TCS in the effluent signifies the challenges treatment systems face in completely removing or degrading TCS to non-detectable levels.
161 ng L−1 in wastewater influent, 23 to 5370 ng L−1 in wastewater effluent, and less than 0.001 to 100 ng L−1 in seawater.3 However, the persistence of the measurable amounts of TCS in the effluent signifies the challenges treatment systems face in completely removing or degrading TCS to non-detectable levels.
TCS and its derivatives have been identified as endocrine disruptors, which are compounds that can interfere with the normal functioning of hormones in organisms.4 These disruptions can affect various physiological processes, potentially leading to adverse health effects in humans and wildlife. Additionally, emerging research has raised concerns about a potential connection between TCS exposure and antibiotic resistance.4 Long-term exposure to TCS results in biological accumulation and high toxicity due to the generation of toxic byproducts, such as chlorinated dioxins and chlorinated phenols, particularly when exposed to heat and sunlight during wastewater treatment processes.5 Therefore, numerous methods have been adopted to eliminate TCS from polluted water sources via chemical decomposition or transformation, like ozonation, Fenton reactions, and microbiological degradation. While these methods can reduce TCS concentrations, they struggle to achieve complete mineralization or elimination of TCS and can potentially produce more toxic byproducts, posing additional environmental risks.6
In contrast, adsorption technology has emerged as a promising and environmentally friendly strategy for removing pollutants like TCS from aqueous solutions. Adsorption involves the adherence of contaminants onto the surface of solid materials (adsorbents), effectively removing them from water. This method often boasts low energy consumption, generates no secondary pollutants, and is highly effective in removing a wide range of emerging contaminants (ECs).7 Developing novel adsorbents with specific properties like high adsorption capacity, low cost, and easy recyclability has garnered considerable attention from the research community. The goal is to create adsorbents that can efficiently and economically remove TCS and other pollutants from water sources. Its adsorption behaviour on various adsorbents has been studied extensively due to concerns about its environmental impact. The common adsorbents are based on several materials, such as activated carbon,6,8,9 biochar,10,11 MOFs7 and other functionalized materials,12 designed specifically for effective pollutant adsorption.
Apart from these adsorbents, few studies have been done on bismuth ferrite [Bi2Fe4O9] (BFO) nanomaterial as an adsorbent for the removal of pollutants like heavy metal ions [Pb(II), Cr(III), Cu(II), As(V)] and methylene blue.13–15 Kong et. al. reported the adsorption capacity of BFO nanoplates as 42.7 mg g−1 for Cu(II) removal.13 In another study by Ting Hu et al., BFO with a coral-like hierarchical structure exhibited excellent adsorption performance toward heavy metal ions [Pb(II), Cr(III), Cu(II), As(V)], achieving the highest adsorption capacity of approximately 214.5 mg g−1 for Pb(II).14 The nanocomposite BFO-GO showed an adsorption capacity of 55.46 mg g−1 for the removal of methylene blue dye.16
BFO with different morphologies, including particles, sheets, plates, cubes, rods, and flowers, can be easily synthesized by tuning the Bi/Fe ratio and NaOH concentration.17–19 Apart from adsorption, it is explored in photocatalysis applications as it exhibits a narrow band gap and thus shows strong absorption in the visible light region. Bi2Fe4O9 has an orthorhombic structure with the space group of Pbam and lattice constants of a = 0.796 nm, b = 0.844 nm, and c = 0.599 nm. The standard unit cell of orthorhombic Bi2Fe4O9 consists of corner-sharing FeO4 tetrahedra and edge-sharing FeO6 octahedra, with Bi3+ ions surrounded by eight oxygen atoms. In the crystal structure of Bi2Fe4O9, the chains of FeO6 octahedra parallel to the c-axis are alternately connected along the c-axis through FeO4 tetrahedra and bismuth atoms.20 BFO contains the 3d transition metal iron (Fe), which possesses a magnetic moment. However, bulk BFO exhibits a non-magnetic nature because of antiferromagnetic coupling between the Fe3+ ions.17 It can be synthesized via hydrothermal methods to obtain different morphologies like sheets, rods, hollow structures, etc.17
BFO nanosheets can efficiently remove TCS from solution through strong surface interactions (e.g., hydrogen bonding, hydrophobic interactions and electrostatic attraction).21 However, adsorption does not mineralize or degrade TCS. Combined adsorption–photocatalysis can degrade and mineralize TCS into smaller, less toxic compounds (e.g., CO2, H2O, and simple organics). Therefore, BFO nanosheets can potentially overcome incomplete mineralization if used in a hybrid adsorption–photocatalytic system, where adsorbed TCS molecules are subsequently degraded in situ under visible light.22
The 2D nanosheet morphology of BFO exposes abundant active sites for pollutant attachment and facilitates easy diffusion and strong interfacial contact between BFO and contaminants (TCS), while surface oxygen vacancies enhance adsorption affinity through electron transfer and coordination effects. Additionally, the surface functional groups (–OH, Bi–O, and Fe–O) provide numerous active sites for pollutant binding through electrostatic attraction, hydrogen bonding and hydrophobic interactions.21 These properties make BFO nanosheets an effective adsorbent.
After adsorption, BFO can be recycled and reused again for adsorption. Furthermore, post-adsorption, BFO can be used as a photocatalyst to degrade the contaminants under visible light.
However, the release of BFO nanoparticles can lead to bioaccumulation, which is an environmental concern. Under severe conditions (acidic environment), small amounts of Bi3+ or Fe3+ ions might leach. Surface coating or immobilization of BFO on stable supports and controlled regeneration help reduce environmental concerns.
The novelty of this work involves the application of BFO material as an adsorbent for TCS removal for the first time, achieving high adsorption capacity at very low adsorbent loading, which has not been reported yet, to our knowledge.
2. Experimental section
2.1 Chemical reagents
Bismuth nitrate pentahydrate [Bi(NO3)3 5H2O], ferric chloride [Fe(Cl3)3·6H2O] and sodium hydroxide (NaOH) were purchased from Merck with 99% purity. Ethylene glycol, ammonium hydroxide solution (28.0–30.0% NH3 basis), and triclosan [5-chloro-2-(2,4-dichlorophenoxy) phenol] (C12H7Cl3O2) were purchased from Sigma-Aldrich. Premium-grade ethanol (100%) was purchased from Hayman. All chemicals were used as received, without further purification. Milli-Q water was used in all the processes.
2.2 Synthesis of Bi2Fe4O9 (BFO) nanosheets
Bismuth ferrite (BFO) nanosheets were synthesized through a hydrothermal approach (as shown in Scheme 1) by following Hua et al.'s method with some modifications.23 The nanosheet synthesis involved using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Bi/Fe (the mole ratio of bismuth and iron precursors). For this, 5 mmol of Bi(NO3)3·5H2O was dissolved in 50 mL of ethylene glycol and stirred for 30 minutes at room temperature (20–25 °C). Subsequently, 5 mmol of Fe(Cl3)3·6H2O was added to the solution and stirred for another 30 minutes. In this mixture, 200 mL of Milli-Q water was added, and the pH was adjusted to 10–11 using a 28–30% ammonium hydroxide solution. The resulting precipitate was separated via centrifugation, washed with Milli-Q water until reaching a pH of 7. The obtained precipitate was re-dispersed in 40 mL of Milli-Q water, followed by addition of 5 M NaOH and continuous stirring of 30 minutes. The resulting suspension was transferred into a 50 mL Teflon-lined steel autoclave and subjected to hydrothermal treatment at 160 °C for 12 hours. After completing the reaction, the autoclave was allowed to cool naturally to room temperature. The resulting product BFO (1
1 ratio of Bi/Fe (the mole ratio of bismuth and iron precursors). For this, 5 mmol of Bi(NO3)3·5H2O was dissolved in 50 mL of ethylene glycol and stirred for 30 minutes at room temperature (20–25 °C). Subsequently, 5 mmol of Fe(Cl3)3·6H2O was added to the solution and stirred for another 30 minutes. In this mixture, 200 mL of Milli-Q water was added, and the pH was adjusted to 10–11 using a 28–30% ammonium hydroxide solution. The resulting precipitate was separated via centrifugation, washed with Milli-Q water until reaching a pH of 7. The obtained precipitate was re-dispersed in 40 mL of Milli-Q water, followed by addition of 5 M NaOH and continuous stirring of 30 minutes. The resulting suspension was transferred into a 50 mL Teflon-lined steel autoclave and subjected to hydrothermal treatment at 160 °C for 12 hours. After completing the reaction, the autoclave was allowed to cool naturally to room temperature. The resulting product BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was collected through centrifugation and washed with Milli-Q water and ethanol multiple times. At last, the obtained powder was dried at 60 °C in an air oven overnight.
1, 5 M NaOH) was collected through centrifugation and washed with Milli-Q water and ethanol multiple times. At last, the obtained powder was dried at 60 °C in an air oven overnight.
 |
| | Scheme 1 Schematic of the synthesis of bismuth ferrite in various Bi/Fe mole ratios and NaOH concentrations. | |
Additionally, the synthesis process of BFO was further explored by adjusting the mole ratio of bismuth and iron precursors (Bi/Fe ratio) to investigate the impact of different Bi/Fe molar ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) while maintaining a constant NaOH concentration of 5 M. Furthermore, investigation for the variations in the NaOH concentration (3 M, 5 M and 8 M) in the synthesis process were examined by maintaining a Bi/Fe mole ratio of 1
1) while maintaining a constant NaOH concentration of 5 M. Furthermore, investigation for the variations in the NaOH concentration (3 M, 5 M and 8 M) in the synthesis process were examined by maintaining a Bi/Fe mole ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while keeping the other parameters unchanged.
1, while keeping the other parameters unchanged.
The synthesis of bismuth ferrite by the hydrothermal process involved: (1) dissociation of the Bi and Fe salts in the ethylene glycol (C2H6O2) solution, (2) formation of Bi(OH)3 and Fe(OH)3 during the addition of water and ammonium hydroxide, and (3) formation of Bi2Fe4O9 in the presence of NaOH during hydrothermal treatment.24 The chemical reactions (eqn (1)–(4)) involved in the synthesis of bismuth ferrite are as follows:
| | | Bi(NO3)3 5H2O + C2H6O2 → [Bi(C2H5O2)]2+ + 3NO3− + H+ | (1) |
| | | FeCl3 6H2O → [Fe(H2O)6]3+ + 3Cl− | (2) |
| | | [Bi(C2H5O2]2+ + [Fe(H2O)6]3+ + NH4OH → Bi(OH)3 + Fe(OH)3 + NH3 + C2H6O2 | (3) |
| |  | (4) |
2.3 Preparation of the TCS stock solution
TCS has minimal solubility in water (<10 mg L−1), but it is completely soluble in ethanol, as shown in Table 1, which represents the physical and chemical properties of TCS.25 A stock solution of 1000 mg L−1 TCS was prepared by dissolving 50 mg of TCS powder in 50 mL premium-grade ethanol (100%). The stock solution was preserved in a fridge. The sample solutions were prepared by mixing the stock solution with Millipore water to achieve the desired concentration. Stock solutions with varying ethanol concentrations (e.g., 5% and 10%) were previously tested but found to be unstable, as the TCS powder began to precipitate after 4–5 hours, making them unsuitable for further solution preparation and adsorption analysis. Therefore, we prepared the stock solution in pure ethanol.
Table 1 Physical and chemical characteristics of TCS25
| Chemical |
Triclosan |
| IUPAC name |
5-Chloro-2-(2,4-dichloro phenoxy)phenol |
| Chemical structure |
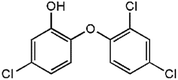
|
| Chemical formula |
C12H7Cl3O2 |
| Molecular weight |
289.54 |
| Appearance |
White solid |
| Melting point |
55–57 °C |
| Boiling point |
120 °C |
| Solubility |
Slightly soluble in water (10 mg L−1 or ppm at 20 °C), high solubility in ethanol, methanol, and diethyl ether |
2.4 Adsorption isotherms
Adsorption involves the mass transfer of adsorbate from the bulk solution to the interior surface of the porous adsorbent, where adsorption takes place. There is no further net adsorption after the solution and adsorbent reach the thermodynamic equilibrium of adsorbate concentration. The concentrations of adsorbent and adsorbate in the system, along with parameters like pH, viscosity, and temperature, define this equilibrium. The most essential characteristic of the adsorbate–adsorbent interaction is the adsorption equilibrium. Consequently, the thermodynamic equilibrium serves as the foundation for the development of theoretical and empirical models that explain reversible adsorption.
An adsorption isotherm describes how the solute (TCS) molecules interact with the adsorbent surface at a constant temperature. To study the interaction behavior and explain the adsorption process, some important isotherm models like Langmuir, Freundlich, Temkin, Redlich–Peterson and Dubinin–Radushkevich (D–R) isotherms were employed.
2.4.1 Langmuir adsorption isotherm.
Langmuir adsorption describes monolayer adsorption on the adsorbent surface containing a finite number of active sites with no further interaction between the adsorbed species. This can express the adsorbent surface characteristics and its affinity for the adsorbate. Langmuir adsorption can be represented by the following eqn (5).8,10,26,27| | 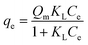 | (5) |
Here qe and Qm are the amount of TCS adsorbed at equilibrium time (mg g−1) and the maximum amount of TCS adsorbed per unit mass of adsorbent, respectively. KL and Ce are the Langmuir constant related to the binding energy (L mg−1) and the TCS concentration at equilibrium time (mg L−1). The equilibrium parameter (RL) (eqn (6)), also known as the separation factor or equilibrium parameter, is a dimensionless constant that is used to define the basic characteristics of the Langmuir isotherm. The value of RL signifies the nature of adsorption: favorable if 0 < RL < 1, linear if RL = 1, unfavorable if RL > 1 and irreversible if RL = 0. It can be calculated as| |  | (6) |
In our study, the value of RL was found to be 0.040 at the initial concentration of 200 mg L−1, which is between 0 to 1, indicating that adsorption is favorable.
2.4.2 Freundlich adsorption isotherm.
The Freundlich isotherm is an empirical model used to describe the adsorption of molecules from a solution onto a solid surface. It is expressed as an equation relating the amount of substance adsorbed onto the surface of the adsorbent to the concentration of the substance in the solution. The Freundlich isotherm is represented by eqn (7):8,10,26,27| | 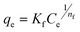 | (7) |
where Kf is the Freundlich isotherm constant related to adsorption capacity ((mg g−1) (L mg−1)1/n), and  denotes the adsorption intensity.
denotes the adsorption intensity.
The Freundlich isotherm does not adhere to the assumptions of ideal adsorption. It is versatile as it accounts for multilayer adsorption and non-uniform surface energies. Its importance lies in its ability to describe adsorption on heterogeneous surfaces with high accuracy compared to simpler models like the Langmuir isotherm. The n value reflects the adsorption intensity: if nf > 1, adsorption is favorable; if nf < 1, it is unfavorable.
2.4.3 Temkin adsorption isotherm.
The Temkin isotherm is another empirical model used to describe the adsorption of molecules from a solution onto a solid surface. It considers the effects of indirect interactions between the adsorbate molecules on a heterogeneous surface. The Temkin isotherm can be represented by eqn (8):8,10,27| |  | (8) |
where Kt is the equilibrium binding constant (L g−1), b1 is the adsorption heat (kJ mol−1), R is the gas constant (8.314 J mol−1 K−1), and T is the absolute temperature (298 K).
The Temkin isotherm assumes a linear decrease in adsorption energy with coverage due to adsorbate–adsorbent interactions. This model is particularly useful for describing systems where interactions between adsorbate molecules play a significant role in the adsorption process.
2.4.4 Redlich–Peterson isotherm.
The Redlich–Peterson isotherm [eqn (9)] is an empirical model used to describe the adsorption of molecules from a solution onto a solid surface. It is a modification of the Freundlich isotherm and provides a more flexible equation to fit a wider range of experimental data.10| |  | (9) |
Here, KR (L g−1) and A (L mg−1) are the Redlich–Peterson constants, KR/A indicates the removal capacity, and g is the Redlich–Peterson constant related to the adsorption intensity. The Redlich–Peterson isotherm allows a better fit of experimental data than some other models because it introduces an additional parameter A, which enhances its flexibility. This flexibility is crucial in cases where the adsorption behavior does not strictly adhere to the assumptions of simpler models.
2.4.5 Dubinin–Radushkevich isotherm.
The Dubinin–Radushkevich (D–R) isotherm is a model based on the assumption that the adsorption energy is not constant but varies exponentially with surface coverage. The Dubinin–Radushkevich isotherm describes physical adsorption processes occurring in systems where the adsorbent surface is not uniform. The mathematical expression and its linearized form are given as eqn (10) and (11), respectively.8,27| | | ln(qe) = ln(qm) − Kε2 | (11) |
| |  | (12) |
| |  | (13) |
Here, ε is the Polanyi potential (eqn (12)), K is the activity coefficient, and E denotes the mean free adsorption energy (kJ mol−1) (eqn (13)). E < 8 corresponds to physisorption, 8 < E < 16 indicates that adsorption involves ion exchange, and E > 8 represents chemisorption.
2.4.6 Boyd isotherm.
The Boyd model is utilized to investigate the actual rate-controlling step involved in the adsorption process, either by film diffusion or intraparticle diffusion. Eqn (14) represents the Boyd model, which is used to analyze the experimental adsorption data.13,28| | 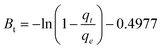 | (14) |
Here, qe (mg g−1) is the adsorption capacity at equilibrium, and qt (mg g−1) is the adsorption capacity at time t. Bt is the function of the fraction of solute adsorbed at different times. The calculated Bt values are plotted against time (t). The linearity of this plot offers important information regarding the rate-controlling step. If the linear fitting is a straight line and passes through the origin, it indicates that intraparticle diffusion (pore diffusion) is the rate-controlling step in the adsorption process. If the fitting of the data is nonlinear or linear but does not pass through the origin, it indicates involvement of film diffusion or external mass transport, which will be the rate-limiting step in the adsorption process.28,29
2.5 Adsorption kinetics
Adsorption kinetics refers to the understanding of how quickly molecules are captured or adsorbed onto the surface of an adsorbent material. The experiment data of the TCS adsorption experiment were fitted by applying various models, including the pseudo-first-order (PFO) [eqn (15)] and pseudo-second-order (PSO) models [eqn (16)].8,10| |  | (16) |
Here, qe is the amount of TCS removed at equilibrium time (mg g−1), k1 is the PFO rate constant (1/h), and k2 is the PSO rate constant (g mg−1 h−1).
2.6 Batch adsorption experiments
TCS was used to perform the pollutant adsorption test of the different as-prepared BFO materials. Briefly, 14 mg of each adsorbent (0.2 g L−1) was dispersed in a 200 mg L−1 TCS (70 mL) solution in a glass Petri dish and stirred at 300 rpm for an adsorption analysis duration of 180 minutes in the dark at room temperature (25 °C). During the adsorption experiments, each Petri dish was covered with another glass Petri dish to avoid ethanol evaporation. Next, 2 mL of the sample was taken out at a fixed interval of 30 minutes, centrifuged, and filtered using a 0.22 µm filter to remove the adsorbent before absorbance measurement. The absorbance of the samples was measured using a UV–vis spectrophotometer during the adsorption process, and the concentration of TCS was calculated from the calibration curve (see SI Fig. S1). The peak wavelength at maximum absorbance for TCS was located at 280 nm. The adsorption capacity of TCS (mg of TCS g−1 of adsorbate) at equilibrium and time (t) was calculated using the following eqn (17) and (18):8,30| |  | (17) |
| |  | (18) |
qe is the amount of TCS adsorbed per gram of adsorbent after achieving the equilibrium (mg g−1), and qt is the amount of TCS adsorbed per gram of adsorbent at time t (mg g−1). C0, Ceq. and Ct are the initial TCS concentration (mg L−1), the equilibrium concentration of TCS (mg L−1), and the TCS concentration at time t (mg L−1), respectively. V and w are the TCS solution volume (L) and weight of the adsorbent (g), respectively. The percentage adsorption was calculated using the following eqn (19):| | 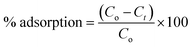 | (19) |
To explore the influence of the initial concentration of TCS on the adsorption capacity of BFO materials, initial concentrations of 100 mg L−1, 150 mg L−1, 185 mg L−1, 190 mg L−1, 195 mg L−1 and 200 mg L−1 were selected for the study. Other parameters were held constant throughout the study. The impact of the initial pH of the TCS solution (pH = 3, 6, and 8) on the adsorption of TCS was examined by adjusting the pH using 0.1 M HNO3 and NH4OH solutions. This investigation was conducted at an initial concentration of 200 mg L−1 and an adsorbent loading of 0.2 g L−1. However, due to very small adsorbent loading (0.2 g L−1), the volume of the adsorbent was negligible compared with the total solution volume; thus, no volume correction was applied in the adsorption calculations. The adsorption results indicated that at pH 3, the adsorption of TCS on BFO was more effective compared to pH 6 and 8. Subsequently, to further explore the influence of adsorbent loading (0.2, 0.25, 0.3 g L−1) on the adsorption of TCS on BFO, investigations were carried out at pH 3 and an initial concentration of 200 mg L−1.
2.7 Data analysis
The concentration of TCS was estimated using the calibration curve equation provided in the SI. The adsorption capacity and % adsorption were calculated using eqn (16)–(18), respectively. The adsorption isotherm models and kinetic data were fitted using Origin software.
3. Material characterization
Powder X-ray diffraction analysis of the as-prepared samples was done using Cu-Kα as the X-ray source (λ = 1.5406 Å) (XRD, X'Pert Pro, PAN analytical). The morphology of the Bi2Fe4O9 samples was recorded using a field-emission scanning electron microscope (FEI NOVA NANO SEM 450, FESEM). The prepared samples were gold-coated (∼10 nm) before the SEM analysis. The elemental analysis and mapping of the elements present in the samples were done using energy-dispersive X-ray spectroscopy (EDX linked to FESEM, Oxford Instrument). Surface area and pore size distribution (PSD) analyses were carried out using the Brunauer–Emmett–Teller (BET) (Quanta Chrome, USA) instrument. A Zeta potentiometer (Malvern, ZS90) was used to measure the zeta potential of the samples. The functional group analysis of samples was performed using FTIR spectroscopy (PerkinElmer, Spectrum Two UATR).
4. Results and discussion
4.1 XRD analysis
The high crystallinity and purity of the as-synthesized BFO samples were measured in the 2θ range of 10°–80°. Fig. 1(a) and (b) show the XRD patterns of the as-prepared BFO samples with variations in the Bi/Fe molar ratio and NaOH concentration, respectively. In Fig. 1(a), the diffraction patterns of the samples with Bi/Fe ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 match well with the standard data (JCPDS no. 25–0090), which is the pure phase of Bi2Fe4O9 ascribed to its orthorhombic structure (space group Pbam; lattice constant a = 7.965 Å, b = 8.440 Å and c = 5.994 Å). The diffraction pattern observed at a Bi/Fe ratio of 2
2 match well with the standard data (JCPDS no. 25–0090), which is the pure phase of Bi2Fe4O9 ascribed to its orthorhombic structure (space group Pbam; lattice constant a = 7.965 Å, b = 8.440 Å and c = 5.994 Å). The diffraction pattern observed at a Bi/Fe ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 matches the standard data (JCPDS no. 046-0416), which is ascribed to the Bi25FeO40 nanomaterial. In Fig. 1(b), the diffraction patterns of samples having a Bi/Fe ratio of 1
1 matches the standard data (JCPDS no. 046-0416), which is ascribed to the Bi25FeO40 nanomaterial. In Fig. 1(b), the diffraction patterns of samples having a Bi/Fe ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and different NaOH concentrations match the standard data (JCPDS no. 25-0090), which is the pure phase of Bi2Fe4O9. However, the crystallinity of the samples changed with the variation in the NaOH concentration. The sample with 5 M NaOH concentration showed higher crystallinity than samples with 3 M and 8 M NaOH concentrations. This may be due to controlled nucleation and crystal growth, resulting in the formation of well-ordered square-shaped crystal structures of BFO NSs at 5 M NaOH.
1 and different NaOH concentrations match the standard data (JCPDS no. 25-0090), which is the pure phase of Bi2Fe4O9. However, the crystallinity of the samples changed with the variation in the NaOH concentration. The sample with 5 M NaOH concentration showed higher crystallinity than samples with 3 M and 8 M NaOH concentrations. This may be due to controlled nucleation and crystal growth, resulting in the formation of well-ordered square-shaped crystal structures of BFO NSs at 5 M NaOH.
 |
| | Fig. 1 XRD patterns of samples (a) with different Bi/Fe ratios and (b) with different NaOH concentrations. | |
The crystallite size of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was calculated using the Debye–Scherrer eqn (20) and is presented in Table S1 (SI).31
1, 5 M NaOH) was calculated using the Debye–Scherrer eqn (20) and is presented in Table S1 (SI).31
| |  | (20) |
Here,
D represents the crystallite size (nm),
k is the shape factor (value taken as 0.9), lambda (
λ = 1.5406 Å) is the wavelength of the incident X-rays, theta (
θ) is the angle of diffraction (radian), and
β (radian) indicates the full-width at half maxima (FWHM) of the characteristic peaks (121 and 211) determined from the XRD data fitted using the Origin software.
4.2 FESEM analysis
FESEM was used to examine the surface morphology of the prepared adsorbents. Fig. 2 illustrates the varying morphologies of the BFO materials with different Bi/Fe ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 2
2, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and NaOH molar concentrations (3 M, 5 M, and 8 M). The Bi/Fe ratio plays a pivotal role in dictating the resulting morphology. For instance, a 1
1) and NaOH molar concentrations (3 M, 5 M, and 8 M). The Bi/Fe ratio plays a pivotal role in dictating the resulting morphology. For instance, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi/Fe ratio yielded uniform 2-D nanosheets [Fig. 2(a)], with an average thickness of about 47 nm. In contrast, a 1
1 Bi/Fe ratio yielded uniform 2-D nanosheets [Fig. 2(a)], with an average thickness of about 47 nm. In contrast, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio produced square or rectangular cubes [Fig. 2(b)], with an average thickness of around 237 nm. Moreover, a 2
2 ratio produced square or rectangular cubes [Fig. 2(b)], with an average thickness of around 237 nm. Moreover, a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio led to the formation of clusters [Fig. 2(c)] comprising small nanosheets. Notably, when the NaOH concentration was adjusted while maintaining a fixed Bi/Fe ratio of 1
1 ratio led to the formation of clusters [Fig. 2(c)] comprising small nanosheets. Notably, when the NaOH concentration was adjusted while maintaining a fixed Bi/Fe ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, it significantly influenced material thickness. At NaOH concentrations of 3 M, 5 M, and 8 M [Fig. 2(d)–(f)], the thickness decreased, measuring average values of 128 nm, 47 nm, and 42 nm, respectively, as shown in Fig. S2. The average length of the BFO (1
1, it significantly influenced material thickness. At NaOH concentrations of 3 M, 5 M, and 8 M [Fig. 2(d)–(f)], the thickness decreased, measuring average values of 128 nm, 47 nm, and 42 nm, respectively, as shown in Fig. S2. The average length of the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was estimated to be 580 nm or 0.58 µm, as shown in Fig. S3. Particularly, at 5 M and 8 M NaOH concentrations, the material manifested as nanosheets.
1, 5 M NaOH) was estimated to be 580 nm or 0.58 µm, as shown in Fig. S3. Particularly, at 5 M and 8 M NaOH concentrations, the material manifested as nanosheets.
 |
| | Fig. 2 FESEM images of (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1 1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2 2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1 1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), (e) BFO (1 1, 3 M NaOH), (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), and (f) BFO (1 1, 5 M NaOH), and (f) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH). 1, 8 M NaOH). | |
4.3 FTIR data
Fig. 3 presents the FTIR data of the as-prepared BFO samples. In the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), BFO (1
1, 5 M NaOH), BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) and BFO (1
1, 3 M NaOH) and BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) samples, the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to the Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively.32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33–35 BFO (1
1, 8 M NaOH) samples, the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to the Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively.32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33–35 BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) also has the same IR spectra as the above three samples, but with a small shift in wavenumbers to 803 cm−1 and 609 cm−1. This shift may be due to excess Fe present while using a 1
2, 5 M NaOH) also has the same IR spectra as the above three samples, but with a small shift in wavenumbers to 803 cm−1 and 609 cm−1. This shift may be due to excess Fe present while using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Bi/Fe ratio, which alters the Fe–O stretching and Fe–O–Fe bending vibrations. Moreover, BFO (2
2 Bi/Fe ratio, which alters the Fe–O stretching and Fe–O–Fe bending vibrations. Moreover, BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) exhibited a different IR spectrum, corresponding to Bi25FeO40. The three main absorption bands within the 400–700 cm−1 zone were identified as typical absorptions associated with Bi–O and Fe–O. Specifically, the robust absorption peaks at 461 cm−1 and 522 cm−1 are attributed to Bi–O vibration modes, while the additional peak at 578 cm−1 corresponds to the stretching vibration of the Fe–O bond.33 These findings from the XRD data collectively highlight the cubic nature of selenite-type Bi25FeO40.
1, 5 M NaOH) exhibited a different IR spectrum, corresponding to Bi25FeO40. The three main absorption bands within the 400–700 cm−1 zone were identified as typical absorptions associated with Bi–O and Fe–O. Specifically, the robust absorption peaks at 461 cm−1 and 522 cm−1 are attributed to Bi–O vibration modes, while the additional peak at 578 cm−1 corresponds to the stretching vibration of the Fe–O bond.33 These findings from the XRD data collectively highlight the cubic nature of selenite-type Bi25FeO40.
 |
| | Fig. 3 FTIR spectra of different BFO samples. | |
4.4 BET analysis
The specific surface areas of all synthesized BFO materials were analyzed by the BET multi-point method using N2 adsorption–desorption isotherms. All samples were degassed for 10 hours at 200 °C under high-purity N2 purging before measurement. The pore volume and pore size data were calculated by the Barrett–Joyner–Halenda (BJH) method using the Kelvin equation. Fig. 4 shows the N2 adsorption–desorption isotherms of (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1
1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2
2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1
1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1
1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH). Table S2 presents the BET surface area, average pore size and BJH pore volume details of all BFO samples. As revealed from the BET analysis, the BFO (1
1, 8 M NaOH). Table S2 presents the BET surface area, average pore size and BJH pore volume details of all BFO samples. As revealed from the BET analysis, the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) sample showed the highest BET surface area and average pore size among other samples and was compatible with a type-IV adsorption isotherm having an H3 hysteresis loop.36,37 The BET results indicate that the nanosheets obtained with 5 M and 8 M NaOH had higher surface area and TCS adsorption capacity than the other BFO materials, indicating a direct relationship with the BET surface area.
1, 5 M NaOH) sample showed the highest BET surface area and average pore size among other samples and was compatible with a type-IV adsorption isotherm having an H3 hysteresis loop.36,37 The BET results indicate that the nanosheets obtained with 5 M and 8 M NaOH had higher surface area and TCS adsorption capacity than the other BFO materials, indicating a direct relationship with the BET surface area.
 |
| | Fig. 4 Nitrogen adsorption–desorption (BET) isotherm plots of (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1 1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2 2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1 1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1 1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH). 1, 8 M NaOH). | |
The t-plot (Vadsvs. static thickness) method was used to determine the micropore volume of the material. The slope and intercept of the t-plot represent the external surface area and micropore volume, respectively. All t-plots (Fig. S4) showed negative intercepts except for the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) sample, which indicates that all samples except BFO (1
1, 3 M NaOH) sample, which indicates that all samples except BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) had only mesopore volume and zero micropore volume. The pore size distributions of the samples presented in Fig. 5 show that the pore sizes of the samples were mostly within the range of 2–50 nm, confirming the mesoporous nature of the BFO materials.
1, 3 M NaOH) had only mesopore volume and zero micropore volume. The pore size distributions of the samples presented in Fig. 5 show that the pore sizes of the samples were mostly within the range of 2–50 nm, confirming the mesoporous nature of the BFO materials.
 |
| | Fig. 5 Pore size distribution patterns of (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1 1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2 2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1 1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1 1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH). 1, 8 M NaOH). | |
4.5 Triclosan adsorption results
Various isotherm models, including Langmuir, Freundlich, Temkin, Redlich–Peterson, and Dubinin–Radushkevich (D–R) and Boyd models, were fitted to the experimental data, as depicted in Fig. 6–8. The parameters obtained from these models are detailed in Table S3. In line with the experimental findings (as shown in Table 2), among the various BFO samples, the highest TCS adsorption capacity was determined to be 871.3 mg g−1 for the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) sample. Moreover, other BFO samples, such as BFO (1
1, 5 M NaOH) sample. Moreover, other BFO samples, such as BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), BFO (2
2, 5 M NaOH), BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), BFO (1
1, 5 M NaOH), BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and BFO (1
1, 3 M NaOH), and BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH), exhibited notable adsorption capacities at 827.7, 816.3, 792.8 and 832.1 mg g−1, respectively, indicating considerable adsorption potential. In descending order, the adsorption capacities ranked as follows: BFO (1
1, 8 M NaOH), exhibited notable adsorption capacities at 827.7, 816.3, 792.8 and 832.1 mg g−1, respectively, indicating considerable adsorption potential. In descending order, the adsorption capacities ranked as follows: BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) > BFO (1
1, 8 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) > BFO (2
2, 5 M NaOH) > BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH). The declining TCS adsorption capacity of these BFO samples is mainly due to the decreasing surface area of the samples, which is also verified by the BET data (Table S2).
1, 3 M NaOH). The declining TCS adsorption capacity of these BFO samples is mainly due to the decreasing surface area of the samples, which is also verified by the BET data (Table S2).
 |
| | Fig. 6 TCS adsorption equilibrium curves and fitted isotherms of in (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1 1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), 5 M NaOH, (c) BFO (2 2, 5 M NaOH), 5 M NaOH, (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1 1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1 1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) samples at pH 6 and 298 K. 1, 8 M NaOH) samples at pH 6 and 298 K. | |
 |
| | Fig. 7 D–R isotherm fitted data of TCS adsorption by (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1 1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), 5 M NaOH, (c) BFO (2 2, 5 M NaOH), 5 M NaOH, (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1 1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1 1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) at pH 6 and 298 K. 1, 8 M NaOH) at pH 6 and 298 K. | |
 |
| | Fig. 8 Boyd model fitting for TCS adsorption by BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) at pH 6 and 298 K. 1, 5 M NaOH) at pH 6 and 298 K. | |
Table 2 Adsorption capacities of TCS by different BFO samples (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, T = 298 K)
| Isotherms |
Parameter |
Value of parameters |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) 1, 5 M NaOH) |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) 2, 5 M NaOH) |
BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) 1, 5 M NaOH) |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) 1, 3 M NaOH) |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) 1, 8 M NaOH) |
| Experimental data |
q
m exp (mg g−1) |
871.3 |
827.7 |
816.3 |
792.8 |
832.1 |
The plot of calculated Btvs. time (t) for the adsorption of TCS on BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) is shown in Fig. 8 for the Boyd model analysis. The linear fitted curve did not pass through the origin, implying the contribution of the film diffusion mechanism to the adsorption process of TCS on BFO (1
1, 5 M NaOH) is shown in Fig. 8 for the Boyd model analysis. The linear fitted curve did not pass through the origin, implying the contribution of the film diffusion mechanism to the adsorption process of TCS on BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH).
1, 5 M NaOH).
According to the experimental findings, the maximum capacity was noted for BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity. All the above-stated adsorption isotherm models were then fitted to the average experimental data. Fig. 9(a) and (b) display the equilibrium adsorption isotherm of BFO (1
1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity. All the above-stated adsorption isotherm models were then fitted to the average experimental data. Fig. 9(a) and (b) display the equilibrium adsorption isotherm of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) with error bars and the corresponding fitted isotherm plot, respectively. The fitted isotherm model data is shown in Table 3. The analysis of fitted isotherm models revealed that the Redlich–Peterson model exhibited the best fit for this sample, based on an R2 value of 0.998. The corresponding adsorption capacity (qm) of 852.8 mg g−1 aligned closely with the experimental data. The Dubinin–Radushkevich model provided the mean free adsorption energy (E) value of 0.307 kJ mol−1 for the adsorbent BFO (1
1, 5 M NaOH) with error bars and the corresponding fitted isotherm plot, respectively. The fitted isotherm model data is shown in Table 3. The analysis of fitted isotherm models revealed that the Redlich–Peterson model exhibited the best fit for this sample, based on an R2 value of 0.998. The corresponding adsorption capacity (qm) of 852.8 mg g−1 aligned closely with the experimental data. The Dubinin–Radushkevich model provided the mean free adsorption energy (E) value of 0.307 kJ mol−1 for the adsorbent BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), indicating the preference for physical adsorption.
1, 5 M NaOH), indicating the preference for physical adsorption.
 |
| | Fig. 9 Equilibrium TCS adsorption isotherms of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) at pH 6 and 298 K: (a) experimental data and (b) fitted isotherm model data. 1, 5 M NaOH) at pH 6 and 298 K: (a) experimental data and (b) fitted isotherm model data. | |
Table 3 Adsorption isotherms parameters of TCS on BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, T = 298 K)
1, 5 M NaOH) (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, T = 298 K)
| Isotherm |
Value of parameters |
Average data for BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) 1, 5 M NaOH) |
| Experimental data |
q
m exp (mg g−1) |
858.1 |
| Langmuir |
q
m (mg g−1) |
1154.7 |
|
K
L (L mg−1) |
0.1187 |
|
R
2
|
0.991 |
| Freundlich |
n
|
2.6821 |
|
K
f ((mg g−1) (L mg−1)1/n |
261.194 |
|
R
2
|
0.979 |
| Temkin |
K
t
(L g−1) |
0.982 |
|
b
1 (kJ mol−1) |
9.14 |
|
R
2
|
0.987 |
| Redlich–Peterson |
K
r (L g−1) |
85.071 |
|
A (kJ mol−1) |
0.00756 |
|
g
|
1.6409 |
|
R
2
|
0.998 |
| Dubinin–Radushkevich |
q
m (mg g−1) |
895.8 |
|
K (J mol−1)2 |
5.3099 × 10−6 |
|
E (kJ mol−1) |
0.307 |
|
R
2
|
0.999 |
4.6 Adsorption kinetics results
The contact time between the adsorbent and adsorbate significantly influences the adsorption process. To comprehend how TCS interacts with various BFO materials over time, an adsorption kinetic study was conducted, as depicted in Fig. 10. It was evident from the experimental findings that the adsorption of TCS on BFO materials rapidly rises within the initial 30 minutes, indicating rapid adsorption onto the BFO materials. This acceleration is attributed to the mass transfer driving force originating from the initial concentration disparity between the TCS solution and the available adsorption sites. However, as the contact time prolonged, no obvious change in the adsorption capacity was observed until reaching an equilibrium state in 180 minutes. This slowdown occurs due to the decrease in concentration difference between the two phases and the likelihood that the adsorption sites on the BFO surface approach saturation. Consequently, the interaction between TCS and BFO gradually weakens.
 |
| | Fig. 10 TCS adsorption kinetic data fitting by (a) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1 1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), 5 M NaOH, (c) BFO (2 2, 5 M NaOH), 5 M NaOH, (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1 1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1 1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) at pH 6 and 298 K. 1, 8 M NaOH) at pH 6 and 298 K. | |
The experimental data were fitted using pseudo-first-order (PFO) and pseudo-second-order (PSO) kinetic models to examine the adsorption kinetics of TCS on various BFO materials. The parameters obtained from this kinetic study are detailed in Table 4. While both kinetic models demonstrated satisfactory fits to the experimental data, the PSO model exhibited notably strong agreement with the experimental adsorption capacity for BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), achieving an R2 value of 0.998. Furthermore, other variants, such as BFO (1
1, 5 M NaOH), achieving an R2 value of 0.998. Furthermore, other variants, such as BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), BFO (2
2, 5 M NaOH), BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), and BFO (1
1, 5 M NaOH), and BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH), also displayed good fits with the PSO model, whereas BFO (1
1, 8 M NaOH), also displayed good fits with the PSO model, whereas BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) aligned better with the PFO model based on their respective R2 values. Notably, the qe values calculated from the PSO model closely matched the experimental qe values. Hence, the PSO model emerged as the most accurate in predicting the adsorption kinetics of TCS onto BFO materials.
1, 3 M NaOH) aligned better with the PFO model based on their respective R2 values. Notably, the qe values calculated from the PSO model closely matched the experimental qe values. Hence, the PSO model emerged as the most accurate in predicting the adsorption kinetics of TCS onto BFO materials.
Table 4 Adsorption kinetic parameters of TCS on different BFO samples (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, T = 298 K)
| Samples |
Pseudo-first order |
Pseudo-second order |
|
q
e (mg g−1) |
k
1 (h−1) |
R
2
|
q
e (mg g−1) |
k
2 (g mg−1 h−1) |
R
2
|
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) 1, 5 M NaOH) |
850.7 |
5.41 |
0.997 |
873.7 |
0.0234 |
0.998 |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) 2, 5 M NaOH) |
816.7 |
5.40 |
0.997 |
840.5 |
0.0228 |
0.998 |
BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) 1, 5 M NaOH) |
801.6 |
4.98 |
0.997 |
827.1 |
0.0204 |
0.998 |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) 1, 3 M NaOH) |
786.4 |
7.38 |
0.997 |
788.4 |
0.1524 |
0.996 |
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) 1, 8 M NaOH) |
812.5 |
04.11 |
0.997 |
854.9 |
0.0114 |
0.999 |
According to the experimental findings, the maximum capacity was noted for BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity, and the average kinetic data were plotted (Fig. 11) till the equilibrium time of 180 minutes. The fitted kinetic data for PFO and PSO are shown in Table 5.
1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity, and the average kinetic data were plotted (Fig. 11) till the equilibrium time of 180 minutes. The fitted kinetic data for PFO and PSO are shown in Table 5.
 |
| | Fig. 11 TCS adsorption data for BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) at pH 6 and 298 K: (a) experimental kinetic data and (b) kinetic fitting data. 1, 5 M NaOH) at pH 6 and 298 K: (a) experimental kinetic data and (b) kinetic fitting data. | |
Table 5 Adsorption kinetic parameters of TCS on BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) sample (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, pH = 6, T = 298 K)
1, 5 M NaOH) sample (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, pH = 6, T = 298 K)
| Samples |
Pseudo-first order |
Pseudo-second order |
|
q
e (mg g−1) |
k
1 (h−1) |
R
2
|
q
e (mg g−1) |
k
2 (g mg−1 h−1) |
R
2
|
BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) 1, 5 M NaOH) |
849.3 |
3.55 |
0.996 |
911.6 |
0.00754 |
0.999 |
4.7 Effect of initial concentration
As shown in Fig. 12(a), the adsorption capacity (qe) exhibited a linear increase with the rise in initial concentration. As the initial concentration of TCS increased from 100 to 200 mg L−1, it led to a corresponding increase in adsorption capacity, escalating from 467 mg g−1 to 858 mg g−1. This improved adsorption capacity with increased initial concentration is attributed to the concentration acting as a driving force, effectively overcoming the mass transfer resistance between the aqueous and solid phases.38 Consequently, a higher initial concentration exerts a stronger driving force, resulting in an elevated adsorption capacity.
 |
| | Fig. 12 Effects of (a) initial concentration, (b) pH, (c) zeta potential, and (d) adsorbent loading of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH). 1, 5 M NaOH). | |
4.8 Effect of pH
The pH significantly impacts pollutant adsorption in water by altering the surface charge of the adsorbent (BFO) and the adsorbate (TCS molecules). The experimental data in Fig. 12(b) show that an increase in pH from 3 to 8 led to a reduction in the adsorption capacity of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) from 903 mg g−1 to 764 mg g−1. In general, elevated pH levels can lead to increased ionization, causing the surface functional groups to become partially or fully deprotonated, consequently resulting in the accumulation of negative charges.39 As a result, alterations in solution pH affect the dissociation of TCS molecules. It is worth noting that TCS (with a pKa of 8.14) doesn't dissociate at acidic pH levels. It exists in a molecular (non-dissociate) state at pH less than its pKa and in anionic form at pH greater than the pKa.11 This lack of dissociation at acidic pH reduces electrostatic repulsive interactions, consequently boosting the adsorption capacity. The impact of pH on the adsorption of organic chemicals hinges on various forces, such as electron donor–acceptor (EDA) interactions, charge repulsion, and specific attractive forces like hydrogen bonding and hydrophobic interactions. Thus, the effect of pH on TCS adsorption can be explained by investigating the solution pH, TCS pKa, and the pHpzc of BFO.
1, 5 M NaOH) from 903 mg g−1 to 764 mg g−1. In general, elevated pH levels can lead to increased ionization, causing the surface functional groups to become partially or fully deprotonated, consequently resulting in the accumulation of negative charges.39 As a result, alterations in solution pH affect the dissociation of TCS molecules. It is worth noting that TCS (with a pKa of 8.14) doesn't dissociate at acidic pH levels. It exists in a molecular (non-dissociate) state at pH less than its pKa and in anionic form at pH greater than the pKa.11 This lack of dissociation at acidic pH reduces electrostatic repulsive interactions, consequently boosting the adsorption capacity. The impact of pH on the adsorption of organic chemicals hinges on various forces, such as electron donor–acceptor (EDA) interactions, charge repulsion, and specific attractive forces like hydrogen bonding and hydrophobic interactions. Thus, the effect of pH on TCS adsorption can be explained by investigating the solution pH, TCS pKa, and the pHpzc of BFO.
The point of zero charge (pHpzc) for BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was found to be 8.5 by measuring its zeta potential across various pH values (3, 6, 7, and 9), as illustrated in Fig. 12(c). The surface of BFO is positively charged when pH < 8.5, while it will be negatively charged at pH > 8.5. When adsorption occurs at a pH level below 8.14 (pH < pKa < pHpzc), the solution predominantly contains TCS in its non-dissociated form, while BFO exhibits a positive surface charge. This scenario results in improved adsorption capacity owing to increased attractive interactions, such as hydrogen bonding and hydrophobic interactions, coupled with reduced repulsive electrostatic interactions. In contrast, at pH > pKa, TCS in the solution is in its anionic state, aligning with the negative charge present on the surface of BFO (pH > pHpzc). As a result, electrostatic repulsion opposes attractive interactions, ultimately contributing to a decline in the adsorption capacity of TCS with increasing pH levels.
1, 5 M NaOH) was found to be 8.5 by measuring its zeta potential across various pH values (3, 6, 7, and 9), as illustrated in Fig. 12(c). The surface of BFO is positively charged when pH < 8.5, while it will be negatively charged at pH > 8.5. When adsorption occurs at a pH level below 8.14 (pH < pKa < pHpzc), the solution predominantly contains TCS in its non-dissociated form, while BFO exhibits a positive surface charge. This scenario results in improved adsorption capacity owing to increased attractive interactions, such as hydrogen bonding and hydrophobic interactions, coupled with reduced repulsive electrostatic interactions. In contrast, at pH > pKa, TCS in the solution is in its anionic state, aligning with the negative charge present on the surface of BFO (pH > pHpzc). As a result, electrostatic repulsion opposes attractive interactions, ultimately contributing to a decline in the adsorption capacity of TCS with increasing pH levels.
4.9 Effect of adsorbent loading
Considering the pH study revealed higher adsorption capacity at pH 3, the adsorbent loading variation study was conducted under pH 3, maintaining an initial TCS concentration of 200 mg L−1. With an increase in adsorbent loading from 0.2 g L−1 to 0.3 g L−1, the corresponding adsorption capacity decreased from 903 mg g−1 to 769 mg g−1, as shown in Fig. 12(d). This decline in adsorption capacity at higher adsorbent dosages may be explained by the very less residual adsorption site availability and a diminished concentration gradient between the adsorbent surface and TCS in solution.10 This phenomenon could be a result of overlapping adsorption sites, which reduce the efficacy of adsorption. Similarly, the % adsorption also demonstrated a reduction from 90.3% to 80.6% accordingly. Table 6 summarizes the TCS adsorption capacities of several adsorbents reported in the literature in comparison with the as-prepared BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5M NaOH).
1, 5M NaOH).
Table 6 Comparison of the TCS adsorption capacity of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5M NaOH) with the reported adsorbents in literature
1, 5M NaOH) with the reported adsorbents in literature
| Adsorbent |
Exp. TCS adsorption capacity (mg TCS g−1) |
Initial TCS concentration (mg L−1) |
Catalyst dosage (g L−1) |
Equilibrium time (h) |
pH |
References |
| Food waste biochar (FWB-300) |
55.6 |
200 |
3.33 |
24 |
7 |
10
|
| Kenaf-derived biochar (KNF-750) |
110 |
200 |
1 |
3 |
7 |
11
|
| Multi-walled carbon nanotubes |
157.7 |
8 |
0.05 |
48 |
3 |
39
|
| Palm Kernel shell |
88.85 |
50 |
0.0067 |
12 |
4 |
40
|
| Nitrogen-enriched porous carbons |
205 |
2000 |
1 |
2 |
— |
41
|
| Biochar obtained from sewage sludge |
113 |
10 |
1.25 |
8 |
2 |
42
|
| Optimized activated carbon |
94.1 |
450 |
1 |
4 |
— |
43
|
| Di octadecyl dimethyl ammonium-magadiite |
543 |
10 |
0.0167 |
24 |
— |
44
|
| Di octadecyl dimethyl amm1onium-bentonite |
422 |
| Diatomite |
120 |
400 |
1 |
— |
— |
45
|
| Bismuth ferrite (Bi2Fe4O9) |
903 |
200 |
0.2 |
3 |
3 |
This work |
4.10 Recyclability and reusability
The BFO adsorbent was recycled by centrifuging the solution after adsorption. The material was then washed multiple times with Milli-Q water and ethanol, followed by drying at 60 °C in an air oven overnight. In this study, the reusability tests could not be performed due to the very low adsorbent dosage used (0.2 g L−1, corresponding to ∼14 mg for 70 mL of solution), which resulted in unavoidable material loss during the separation and washing steps. However, to indirectly assess the material stability after adsorption, we analyzed the XRD and FTIR spectra of the used BFO nanosheets.
The XRD patterns of the recycled/washed BFO nanosheets [Fig. S5] showed that the crystalline structure of BFO remained unchanged after TCS adsorption, while the FTIR spectra [Fig. 13(b)] indicated the retention of major surface functional groups, with only minor shifts related to adsorbate interaction, which are explained in Section 5. These results suggest that the BFO nanosheets possess good structural stability and can potentially be regenerated and reused.
 |
| | Fig. 13 FTIR data of (a) TCS, BFO, and TCS adsorbed BFO (TCS + BFO) and (b) fresh and washed BFO after adsorption. | |
5. Adsorption mechanism
The adsorption of TCS on the prepared BFO samples is primarily governed by physical adsorption forces like hydrophobic interaction and hydrogen bonding. Moreover, the E values less than 8 kJ mol−1 in the D-R isotherm model indicate that the adsorption process is driven by weak interactions. Fig. 13(a) represents the FTIR data of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), TCS and TCS absorbed BFO (BFO + TCS), whereas Fig. 13(b) shows the FTIR spectra of fresh and washed BFO after adsorption. For fresh BFO (1
1, 5 M NaOH), TCS and TCS absorbed BFO (BFO + TCS), whereas Fig. 13(b) shows the FTIR spectra of fresh and washed BFO after adsorption. For fresh BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33,46,47
1, 5 M NaOH), the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33,46,47
In the TCS infrared spectrum, the absorption bands at 3311 cm−1 and 3065 cm−1 correspond to the O–H bond and C–H stretching, respectively. The absorption bands in the range of 1600–1400 cm−1 and 1200–950 cm−1 correspond to the C–C ring stretching mode of phenyl rings and C–O stretching, while those at 750–700 cm−1 and 909 cm−1 correspond to C–Cl stretching with a single Cl and aromatic C–Cl stretching, respectively.21,48 The interaction mechanisms between BFO and TCS can be explained by changes in the spectra of spent BFO (TCS + BFO). The absorption bands at 3311 cm−1 and 3065 cm−1 correspond to O–H stretching (hydrogen bond), and C–H stretching in TCS was shifted to 3513 cm−1 and 3092 cm−1 in the spent BFO spectra, indicating that TCS is adsorbed on BFO by hydrogen (O–H) bonding and the multiplicity of weak bonds.21 Furthermore, no additional absorption band was observed in the washed BFO spectrum [in Fig. 13(b)], indicating that physical adsorption plays a key role in the adsorption of TCS on BFO. Table S4 shows the FTIR spectral characteristics of BFO before and after adsorption. Moreover, various new absorption bands appeared with some shifts seen for the spent BFO in the ranges of 400–900 cm−1, associated with Fe–O bond bending, Fe–O–Fe bending and Fe–O stretching.
6. Conclusion
This study focuses on the adsorption of TCS in an aqueous solution onto various bismuth ferrite samples. The experimental adsorption capacities of the different BFO samples were observed to be in the following descending order: BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) > BFO (1
1, 8 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) > BFO (2
2, 5 M NaOH) > BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH). The kinetic analysis revealed the second-order kinetic model to be the best fit for these BFO materials. The adsorption–desorption equilibrium was achieved within 180 minutes, and the Redlich–Peterson model properly described the adsorption isotherms of TCS on BFO. The mean free adsorption energy obtained from the D–R isotherm suggests that the adsorption process in BFO materials involves physical adsorption mechanisms, predominantly hydrogen bonding and electrostatic interactions. The study of pH effects showed that at a lower pH of 3, the interaction between TCS and BFO was enhanced, leading to improved adsorption capacity. Moreover, it was found that lower adsorbent loadings result in higher adsorption capacities. This is attributed to the overlapping of adsorption sites at higher adsorbent loadings, which reduces adsorption effectiveness. The BFO sample with a 1
1, 3 M NaOH). The kinetic analysis revealed the second-order kinetic model to be the best fit for these BFO materials. The adsorption–desorption equilibrium was achieved within 180 minutes, and the Redlich–Peterson model properly described the adsorption isotherms of TCS on BFO. The mean free adsorption energy obtained from the D–R isotherm suggests that the adsorption process in BFO materials involves physical adsorption mechanisms, predominantly hydrogen bonding and electrostatic interactions. The study of pH effects showed that at a lower pH of 3, the interaction between TCS and BFO was enhanced, leading to improved adsorption capacity. Moreover, it was found that lower adsorbent loadings result in higher adsorption capacities. This is attributed to the overlapping of adsorption sites at higher adsorbent loadings, which reduces adsorption effectiveness. The BFO sample with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi/Fe mole ratio and 5 M NaOH concentration exhibited the highest TCS adsorption capacity of 903 mg g−1 at pH 3, with an adsorbent loading of 0.2 g L−1 at a temperature of 298 K. In summary, BFO nanosheets exhibit excellent adsorption capacity toward triclosan, attributed to their active surface sites and nanosheet morphology. These results demonstrate that BFO nanosheets are a promising and environmentally sustainable material for the efficient removal of emerging contaminants from wastewater.
1 Bi/Fe mole ratio and 5 M NaOH concentration exhibited the highest TCS adsorption capacity of 903 mg g−1 at pH 3, with an adsorbent loading of 0.2 g L−1 at a temperature of 298 K. In summary, BFO nanosheets exhibit excellent adsorption capacity toward triclosan, attributed to their active surface sites and nanosheet morphology. These results demonstrate that BFO nanosheets are a promising and environmentally sustainable material for the efficient removal of emerging contaminants from wastewater.
Author contributions
Komal Shukla: conceptualization, writing – original draft, visualization, methodology, investigation, data analysis, Raju Kumar Gupta: supervision, review & editing.
Conflicts of interest
There are no conflicts to declare.
Data availability
All data pertaining to this study have been presented in this manuscript or included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5su00645g.
Acknowledgements
RKG acknowledges the financial assistance from the Department of Science and Technology (DST), India, through the INSPIRE Faculty Award (Project No. IFA-13 ENG-57) and Grant No. DST/TM/WTI/2K16/23(G). The authors acknowledge the financial support from the Kotak School of Sustainability, IIT Kanpur. The authors acknowledge the support from the Department of Science and Technology, Government of India (Project-FIST/2023640) and are grateful to Post Graduate Research Laboratory of Department of Chemical Engineering, IIT Kanpur, for providing access to XRD, FESEM and BET equipment.
References
- K. Shi, H. Zhang, H. Xu, Z. Liu, G. Kan, K. Yu and J. Jiang, Sci. Total Environ., 2022, 842, 156832 CrossRef PubMed.
- M. Li, Y. He, J. Sun, J. Li, J. Bai and C. Zhang, Environ. Sci. Technol., 2019, 53, 3277–3286 CrossRef PubMed.
- H. Montaseri and P. B. C. Forbes, TrAC, Trends Anal. Chem., 2016, 85, 221–231 CrossRef.
- R. U. Halden, Environ. Sci. Technol., 2014, 48, 3603–3611 CrossRef PubMed.
- D. E. Latch, J. L. Packer, W. A. Arnold and K. McNeill, J. Photochem. Photobiol., A, 2003, 158, 63–66 CrossRef.
- Q. Xu, D. Lai, Z. Xing, X. Liu and Y. Wang, Chemosphere, 2023, 310, 136897 CrossRef PubMed.
- S. Y. Al nami and A. Hossan, J. Mol. Liq., 2023, 382, 122065 CrossRef.
- H. Kaur, G. Hippargi, G. R. Pophali and A. Bansiwal, J. Colloid Interface Sci., 2019, 535, 111–121 CrossRef PubMed.
- Y. Liu, X. Zhu, F. Qian, S. Zhang and J. Chen, RSC Adv., 2014, 4, 63620–63626 RSC.
- J.-K. Kang, E.-J. Seo, C.-G. Lee, J.-K. Moon and S. J. Park, Biomass Convers. Biorefin., 2023, 13, 11067–11083 CrossRef.
- E.-J. Cho, J.-K. Kang, J.-K. Moon, B.-H. Um, C.-G. Lee, S. Jeong and S.-J. Park, J. Environ. Chem. Eng., 2021, 9, 106343 CrossRef.
- T. B. Vidovix, E. F. D. Januário, M. F. Araújo, R. Bergamasco and A. M. S. Vieira, Environ. Sci. Pollut. Res., 2022, 29, 46813–46829 CrossRef PubMed.
- M. Kong, H. Song, F. Li, D. Dai and H. Gao, J. Environ. Chem. Eng., 2017, 5, 69–78 CrossRef.
- Z.-T. Hu, Z. Chen, R. Goei, W. Wu and T.-T. Lim, Nanoscale, 2016, 8, 12736–12746 RSC.
- S. Singh, Y. Yadawa and A. Ranjan, J. Environ. Chem., 2023, 11, 109229 CrossRef.
- T. Ahmed and S. Susmita, Azerb. Chem. J., 2023, 78–96, DOI:10.32737/0005-2531-2023-2-78-96.
- T. Wu, L. Liu, M. Pi, D. Zhang and S. Chen, Appl. Surf. Sci., 2016, 377, 253–261 CrossRef.
- X. Zhang, J. Lv, L. Bourgeois, J. Cui, Y. Wu, H. Wang and P. A. Webley, New J. Chem., 2011, 35, 937–941 RSC.
- Q.-J. Ruan and W.-D. Zhang, J. Phys. Chem. C, 2009, 113, 4168–4173 CrossRef.
-
S. Poorva, K. Ashwini, T. Jingyou and T. Guolong, in Magnetic Materials and Magnetic Levitation, ed. S. Dipti Ranjan and N. S. Vasilios, IntechOpen, Rijeka, 2020, p. 670, DOI:10.5772/intechopen.93280.
- N. Aminu, S.-Y. Chan, M. A. Mumuni, N. M. Umar, N. Tanko, S. A. Zauro, A. Aminu and S.-M. Toh, Future J. Pharm. Sci., 2021, 7, 148 CrossRef.
- Z. Liu, B. Wu and Y. Zhu, Mater. Chem. Phys., 2012, 135, 474–478 CrossRef.
- H. Hua, F. Feng, M. Du, Y. Ma, Y. Pu, J. Zhang and X. a. Li, Appl. Surf. Sci., 2021, 541, 148428 CrossRef.
- M. Hojamberdiev, Y. Xu, F. Wang, J. Wang, W. Liu and M. Wang, Ceram.-Silik., 2009, 53, 113–117 Search PubMed.
-
Triclosan, https://www.sigmaaldrich.com/IN/en/product/sigma/72779, 2025.
- L. A. González-Fernández, N. A. Medellín-Castillo, R. Ocampo-Pérez, H. Hernández-Mendoza, M. S. Berber-Mendoza and C. Aldama-Aguilera, J. Environ. Chem., 2021, 9, 106382 CrossRef.
- A. O. Dada, A. P. Olalekan, A. Olatunya and A. O. Dada, J. Appl. Chem., 2012, 3, 38–45 Search PubMed.
-
M. A. Alsharif, in Adsorption - Fundamental Mechanisms and Applications, ed. T. I. Shabatina and Y. Gromova, IntechOpen, London, 2025, DOI:10.5772/intechopen.1008865.
- W. Zhu, J. Liu and M. Li, Sci. World J., 2014, 2014, 485820 Search PubMed.
- J. Ma, J. Zhao, Z. Zhu, L. Li and F. Yu, Environ. Pollut., 2019, 254, 113104 CrossRef PubMed.
- S. Z. Mehmood, M. Arshad, F. M. Alharbi, S. M. Eldin and A. M. Galal, Inorganics, 2023, 11, 134 CrossRef.
- G. Wang, S. Liu, T. He, X. Liu, Q. Deng, Y. Mao and S. Wang, Mater. Res. Bull., 2018, 104, 104–111 CrossRef CAS.
- G. Wang, D. Cheng, T. He, Y. Hu, Q. Deng, Y. Mao and S. Wang, J. Mater. Sci.: Mater. Electron., 2019, 30, 10923–10933 CrossRef CAS.
- L. Di, H. Yang, T. Xian and X. Chen, Micromachines, 2018, 9, 613 CrossRef.
- S. Krishna Rao, E. Meher Abhinav, D. Jaison, A. Sundararaj, M. Santhiya, R. Althaf and C. Gopalakrishnan, Vacuum, 2020, 172, 109109 CrossRef CAS.
- S. Raj and A. N. Samanta, Sep. Purif. Technol., 2025, 371, 133341 CrossRef CAS.
- S. Raj, Y. Chainy, P. Sardar and A. N. Samanta, Surf. Interfaces, 2025, 60, 106011 CrossRef CAS.
- N. K. E. Mohd Khori, T. Hadibarata, M. S. Elshikh, A. A. Al-Ghamdi, Salmiati and Z. Yusop, J. Chin. Chem. Soc., 2018, 65, 951–959 CrossRef CAS.
- S. Zhou, Y. Shao, N. Gao, J. Deng and C. Tan, Clean:Soil, Air, Water, 2013, 41, 539–547 CAS.
- M. Triwiswara, C.-G. Lee, J.-K. Moon and S.-J. Park, Desalin. Water Treat., 2020, 177, 71–79 CrossRef CAS.
- Y. Jiang, Z. Zhang, Y. Zhang, X. Zhou, L. Wang, A. Yasin and L. Zhang, RSC Adv., 2018, 8, 42405–42414 RSC.
- B. Czech, M. Kończak, M. Rakowska and P. Oleszczuk, J. Cleaner Prod., 2021, 288, 125686 CrossRef CAS.
- J. T. C. Yokoyama, A. L. Cazetta, K. C. Bedin, L. Spessato, J. M. Fonseca, P. S. Carraro, A. Ronix, M. C. Silva, T. L. Silva and V. C. Almeida, Ecotoxicol. Environ. Saf., 2019, 172, 403–410 CrossRef CAS PubMed.
- A. Phuekphong, K. Imwiset and M. Ogawa, J. Inorg. Organomet. Polym. Mater., 2021, 31, 1902–1911 CrossRef CAS.
- A. A. Sharipova, S. B. Aidarova, N. Y. Bekturganova, A. Tleuova, M. Kerimkulova, O. Yessimova, T. Kairaliyeva, O. Lygina, S. Lyubchik and R. Miller, Colloids Surf., A, 2017, 532, 97–101 CrossRef CAS.
- L. Di, H. Yang, T. Xian and X. Chen, Micromachines, 2018, 9, 613 CrossRef.
- S. Krishna Rao, E. Meher Abhinav, D. Jaison, A. Sundararaj, M. Santhiya, R. Althaf and C. Gopalakrishnan, Vacuum, 2020, 172 Search PubMed.
- H. Özişik, S. H. Bayari and S. Sağlam, AIP Conf. Proc., 2010, 1203, 1227–1232 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abcde
*abcde
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi/Fe mole ratio and 5 M NaOH concentration demonstrated the maximum TCS adsorption capacity, reaching 903 mg g−1 at pH 3, with a 0.2 g L−1 adsorbent loading at 298 K. This remarkable adsorption capacity of BFO nanosheets with minimal adsorbent loading and material stability validates its strong potential as a sustainable adsorbent for the efficient removal of emerging contaminants, like TCS, from wastewater.
1 Bi/Fe mole ratio and 5 M NaOH concentration demonstrated the maximum TCS adsorption capacity, reaching 903 mg g−1 at pH 3, with a 0.2 g L−1 adsorbent loading at 298 K. This remarkable adsorption capacity of BFO nanosheets with minimal adsorbent loading and material stability validates its strong potential as a sustainable adsorbent for the efficient removal of emerging contaminants, like TCS, from wastewater.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5 M NaOH exhibited a TCS adsorption capacity of 903 mg g−1 in 180 minutes at pH 3 and an adsorbent loading of 0.2 g L−1, which is quite higher than that reported in the literature (average TCS adsorption capacity ∼190 mg g−1). This rapid adsorption of TCS onto BFO occurs due to hydrogen bonding and electrostatic interactions. It offers an environmentally friendly solution that reduces the reliance on toxic chemicals or energy-intensive processes. Moreover, it can be easily regenerated and reused, enhancing its sustainability profile. By integrating BFO into wastewater treatment systems, we can take a step toward cleaner water and a greener future.
1 and 5 M NaOH exhibited a TCS adsorption capacity of 903 mg g−1 in 180 minutes at pH 3 and an adsorbent loading of 0.2 g L−1, which is quite higher than that reported in the literature (average TCS adsorption capacity ∼190 mg g−1). This rapid adsorption of TCS onto BFO occurs due to hydrogen bonding and electrostatic interactions. It offers an environmentally friendly solution that reduces the reliance on toxic chemicals or energy-intensive processes. Moreover, it can be easily regenerated and reused, enhancing its sustainability profile. By integrating BFO into wastewater treatment systems, we can take a step toward cleaner water and a greener future.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ng L−1 in surface waters, 20 to 86
000 ng L−1 in surface waters, 20 to 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 ng L−1 in wastewater influent, 23 to 5370 ng L−1 in wastewater effluent, and less than 0.001 to 100 ng L−1 in seawater.3 However, the persistence of the measurable amounts of TCS in the effluent signifies the challenges treatment systems face in completely removing or degrading TCS to non-detectable levels.
161 ng L−1 in wastewater influent, 23 to 5370 ng L−1 in wastewater effluent, and less than 0.001 to 100 ng L−1 in seawater.3 However, the persistence of the measurable amounts of TCS in the effluent signifies the challenges treatment systems face in completely removing or degrading TCS to non-detectable levels.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Bi/Fe (the mole ratio of bismuth and iron precursors). For this, 5 mmol of Bi(NO3)3·5H2O was dissolved in 50 mL of ethylene glycol and stirred for 30 minutes at room temperature (20–25 °C). Subsequently, 5 mmol of Fe(Cl3)3·6H2O was added to the solution and stirred for another 30 minutes. In this mixture, 200 mL of Milli-Q water was added, and the pH was adjusted to 10–11 using a 28–30% ammonium hydroxide solution. The resulting precipitate was separated via centrifugation, washed with Milli-Q water until reaching a pH of 7. The obtained precipitate was re-dispersed in 40 mL of Milli-Q water, followed by addition of 5 M NaOH and continuous stirring of 30 minutes. The resulting suspension was transferred into a 50 mL Teflon-lined steel autoclave and subjected to hydrothermal treatment at 160 °C for 12 hours. After completing the reaction, the autoclave was allowed to cool naturally to room temperature. The resulting product BFO (1
1 ratio of Bi/Fe (the mole ratio of bismuth and iron precursors). For this, 5 mmol of Bi(NO3)3·5H2O was dissolved in 50 mL of ethylene glycol and stirred for 30 minutes at room temperature (20–25 °C). Subsequently, 5 mmol of Fe(Cl3)3·6H2O was added to the solution and stirred for another 30 minutes. In this mixture, 200 mL of Milli-Q water was added, and the pH was adjusted to 10–11 using a 28–30% ammonium hydroxide solution. The resulting precipitate was separated via centrifugation, washed with Milli-Q water until reaching a pH of 7. The obtained precipitate was re-dispersed in 40 mL of Milli-Q water, followed by addition of 5 M NaOH and continuous stirring of 30 minutes. The resulting suspension was transferred into a 50 mL Teflon-lined steel autoclave and subjected to hydrothermal treatment at 160 °C for 12 hours. After completing the reaction, the autoclave was allowed to cool naturally to room temperature. The resulting product BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was collected through centrifugation and washed with Milli-Q water and ethanol multiple times. At last, the obtained powder was dried at 60 °C in an air oven overnight.
1, 5 M NaOH) was collected through centrifugation and washed with Milli-Q water and ethanol multiple times. At last, the obtained powder was dried at 60 °C in an air oven overnight.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) while maintaining a constant NaOH concentration of 5 M. Furthermore, investigation for the variations in the NaOH concentration (3 M, 5 M and 8 M) in the synthesis process were examined by maintaining a Bi/Fe mole ratio of 1
1) while maintaining a constant NaOH concentration of 5 M. Furthermore, investigation for the variations in the NaOH concentration (3 M, 5 M and 8 M) in the synthesis process were examined by maintaining a Bi/Fe mole ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while keeping the other parameters unchanged.
1, while keeping the other parameters unchanged.
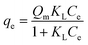

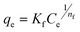
 denotes the adsorption intensity.
denotes the adsorption intensity.




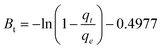



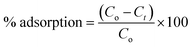
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 match well with the standard data (JCPDS no. 25–0090), which is the pure phase of Bi2Fe4O9 ascribed to its orthorhombic structure (space group Pbam; lattice constant a = 7.965 Å, b = 8.440 Å and c = 5.994 Å). The diffraction pattern observed at a Bi/Fe ratio of 2
2 match well with the standard data (JCPDS no. 25–0090), which is the pure phase of Bi2Fe4O9 ascribed to its orthorhombic structure (space group Pbam; lattice constant a = 7.965 Å, b = 8.440 Å and c = 5.994 Å). The diffraction pattern observed at a Bi/Fe ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 matches the standard data (JCPDS no. 046-0416), which is ascribed to the Bi25FeO40 nanomaterial. In Fig. 1(b), the diffraction patterns of samples having a Bi/Fe ratio of 1
1 matches the standard data (JCPDS no. 046-0416), which is ascribed to the Bi25FeO40 nanomaterial. In Fig. 1(b), the diffraction patterns of samples having a Bi/Fe ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and different NaOH concentrations match the standard data (JCPDS no. 25-0090), which is the pure phase of Bi2Fe4O9. However, the crystallinity of the samples changed with the variation in the NaOH concentration. The sample with 5 M NaOH concentration showed higher crystallinity than samples with 3 M and 8 M NaOH concentrations. This may be due to controlled nucleation and crystal growth, resulting in the formation of well-ordered square-shaped crystal structures of BFO NSs at 5 M NaOH.
1 and different NaOH concentrations match the standard data (JCPDS no. 25-0090), which is the pure phase of Bi2Fe4O9. However, the crystallinity of the samples changed with the variation in the NaOH concentration. The sample with 5 M NaOH concentration showed higher crystallinity than samples with 3 M and 8 M NaOH concentrations. This may be due to controlled nucleation and crystal growth, resulting in the formation of well-ordered square-shaped crystal structures of BFO NSs at 5 M NaOH.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was calculated using the Debye–Scherrer eqn (20) and is presented in Table S1 (SI).31
1, 5 M NaOH) was calculated using the Debye–Scherrer eqn (20) and is presented in Table S1 (SI).31
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 2
2, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and NaOH molar concentrations (3 M, 5 M, and 8 M). The Bi/Fe ratio plays a pivotal role in dictating the resulting morphology. For instance, a 1
1) and NaOH molar concentrations (3 M, 5 M, and 8 M). The Bi/Fe ratio plays a pivotal role in dictating the resulting morphology. For instance, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi/Fe ratio yielded uniform 2-D nanosheets [Fig. 2(a)], with an average thickness of about 47 nm. In contrast, a 1
1 Bi/Fe ratio yielded uniform 2-D nanosheets [Fig. 2(a)], with an average thickness of about 47 nm. In contrast, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio produced square or rectangular cubes [Fig. 2(b)], with an average thickness of around 237 nm. Moreover, a 2
2 ratio produced square or rectangular cubes [Fig. 2(b)], with an average thickness of around 237 nm. Moreover, a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio led to the formation of clusters [Fig. 2(c)] comprising small nanosheets. Notably, when the NaOH concentration was adjusted while maintaining a fixed Bi/Fe ratio of 1
1 ratio led to the formation of clusters [Fig. 2(c)] comprising small nanosheets. Notably, when the NaOH concentration was adjusted while maintaining a fixed Bi/Fe ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, it significantly influenced material thickness. At NaOH concentrations of 3 M, 5 M, and 8 M [Fig. 2(d)–(f)], the thickness decreased, measuring average values of 128 nm, 47 nm, and 42 nm, respectively, as shown in Fig. S2. The average length of the BFO (1
1, it significantly influenced material thickness. At NaOH concentrations of 3 M, 5 M, and 8 M [Fig. 2(d)–(f)], the thickness decreased, measuring average values of 128 nm, 47 nm, and 42 nm, respectively, as shown in Fig. S2. The average length of the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was estimated to be 580 nm or 0.58 µm, as shown in Fig. S3. Particularly, at 5 M and 8 M NaOH concentrations, the material manifested as nanosheets.
1, 5 M NaOH) was estimated to be 580 nm or 0.58 µm, as shown in Fig. S3. Particularly, at 5 M and 8 M NaOH concentrations, the material manifested as nanosheets.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1
1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2
2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1
1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), (e) BFO (1
1, 3 M NaOH), (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), and (f) BFO (1
1, 5 M NaOH), and (f) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH).
1, 8 M NaOH).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), BFO (1
1, 5 M NaOH), BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) and BFO (1
1, 3 M NaOH) and BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) samples, the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to the Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively.32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33–35 BFO (1
1, 8 M NaOH) samples, the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to the Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively.32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33–35 BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) also has the same IR spectra as the above three samples, but with a small shift in wavenumbers to 803 cm−1 and 609 cm−1. This shift may be due to excess Fe present while using a 1
2, 5 M NaOH) also has the same IR spectra as the above three samples, but with a small shift in wavenumbers to 803 cm−1 and 609 cm−1. This shift may be due to excess Fe present while using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Bi/Fe ratio, which alters the Fe–O stretching and Fe–O–Fe bending vibrations. Moreover, BFO (2
2 Bi/Fe ratio, which alters the Fe–O stretching and Fe–O–Fe bending vibrations. Moreover, BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) exhibited a different IR spectrum, corresponding to Bi25FeO40. The three main absorption bands within the 400–700 cm−1 zone were identified as typical absorptions associated with Bi–O and Fe–O. Specifically, the robust absorption peaks at 461 cm−1 and 522 cm−1 are attributed to Bi–O vibration modes, while the additional peak at 578 cm−1 corresponds to the stretching vibration of the Fe–O bond.33 These findings from the XRD data collectively highlight the cubic nature of selenite-type Bi25FeO40.
1, 5 M NaOH) exhibited a different IR spectrum, corresponding to Bi25FeO40. The three main absorption bands within the 400–700 cm−1 zone were identified as typical absorptions associated with Bi–O and Fe–O. Specifically, the robust absorption peaks at 461 cm−1 and 522 cm−1 are attributed to Bi–O vibration modes, while the additional peak at 578 cm−1 corresponds to the stretching vibration of the Fe–O bond.33 These findings from the XRD data collectively highlight the cubic nature of selenite-type Bi25FeO40.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1
1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2
2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1
1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1
1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH). Table S2 presents the BET surface area, average pore size and BJH pore volume details of all BFO samples. As revealed from the BET analysis, the BFO (1
1, 8 M NaOH). Table S2 presents the BET surface area, average pore size and BJH pore volume details of all BFO samples. As revealed from the BET analysis, the BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) sample showed the highest BET surface area and average pore size among other samples and was compatible with a type-IV adsorption isotherm having an H3 hysteresis loop.36,37 The BET results indicate that the nanosheets obtained with 5 M and 8 M NaOH had higher surface area and TCS adsorption capacity than the other BFO materials, indicating a direct relationship with the BET surface area.
1, 5 M NaOH) sample showed the highest BET surface area and average pore size among other samples and was compatible with a type-IV adsorption isotherm having an H3 hysteresis loop.36,37 The BET results indicate that the nanosheets obtained with 5 M and 8 M NaOH had higher surface area and TCS adsorption capacity than the other BFO materials, indicating a direct relationship with the BET surface area.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1
1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2
2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1
1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1
1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH).
1, 8 M NaOH).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) sample, which indicates that all samples except BFO (1
1, 3 M NaOH) sample, which indicates that all samples except BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) had only mesopore volume and zero micropore volume. The pore size distributions of the samples presented in Fig. 5 show that the pore sizes of the samples were mostly within the range of 2–50 nm, confirming the mesoporous nature of the BFO materials.
1, 3 M NaOH) had only mesopore volume and zero micropore volume. The pore size distributions of the samples presented in Fig. 5 show that the pore sizes of the samples were mostly within the range of 2–50 nm, confirming the mesoporous nature of the BFO materials.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (b) BFO (1
1, 5 M NaOH), (b) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), (c) BFO (2
2, 5 M NaOH), (c) BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), (d) BFO (1
1, 5 M NaOH), (d) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and (e) BFO (1
1, 3 M NaOH), and (e) BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH).
1, 8 M NaOH).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) sample. Moreover, other BFO samples, such as BFO (1
1, 5 M NaOH) sample. Moreover, other BFO samples, such as BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), BFO (2
2, 5 M NaOH), BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), BFO (1
1, 5 M NaOH), BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH), and BFO (1
1, 3 M NaOH), and BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH), exhibited notable adsorption capacities at 827.7, 816.3, 792.8 and 832.1 mg g−1, respectively, indicating considerable adsorption potential. In descending order, the adsorption capacities ranked as follows: BFO (1
1, 8 M NaOH), exhibited notable adsorption capacities at 827.7, 816.3, 792.8 and 832.1 mg g−1, respectively, indicating considerable adsorption potential. In descending order, the adsorption capacities ranked as follows: BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) > BFO (1
1, 8 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) > BFO (2
2, 5 M NaOH) > BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH). The declining TCS adsorption capacity of these BFO samples is mainly due to the decreasing surface area of the samples, which is also verified by the BET data (Table S2).
1, 3 M NaOH). The declining TCS adsorption capacity of these BFO samples is mainly due to the decreasing surface area of the samples, which is also verified by the BET data (Table S2).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH)
1, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH)
2, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH)
1, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH)
1, 3 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH)
1, 8 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) is shown in Fig. 8 for the Boyd model analysis. The linear fitted curve did not pass through the origin, implying the contribution of the film diffusion mechanism to the adsorption process of TCS on BFO (1
1, 5 M NaOH) is shown in Fig. 8 for the Boyd model analysis. The linear fitted curve did not pass through the origin, implying the contribution of the film diffusion mechanism to the adsorption process of TCS on BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH).
1, 5 M NaOH).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity. All the above-stated adsorption isotherm models were then fitted to the average experimental data. Fig. 9(a) and (b) display the equilibrium adsorption isotherm of BFO (1
1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity. All the above-stated adsorption isotherm models were then fitted to the average experimental data. Fig. 9(a) and (b) display the equilibrium adsorption isotherm of BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) with error bars and the corresponding fitted isotherm plot, respectively. The fitted isotherm model data is shown in Table 3. The analysis of fitted isotherm models revealed that the Redlich–Peterson model exhibited the best fit for this sample, based on an R2 value of 0.998. The corresponding adsorption capacity (qm) of 852.8 mg g−1 aligned closely with the experimental data. The Dubinin–Radushkevich model provided the mean free adsorption energy (E) value of 0.307 kJ mol−1 for the adsorbent BFO (1
1, 5 M NaOH) with error bars and the corresponding fitted isotherm plot, respectively. The fitted isotherm model data is shown in Table 3. The analysis of fitted isotherm models revealed that the Redlich–Peterson model exhibited the best fit for this sample, based on an R2 value of 0.998. The corresponding adsorption capacity (qm) of 852.8 mg g−1 aligned closely with the experimental data. The Dubinin–Radushkevich model provided the mean free adsorption energy (E) value of 0.307 kJ mol−1 for the adsorbent BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), indicating the preference for physical adsorption.
1, 5 M NaOH), indicating the preference for physical adsorption.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) at pH 6 and 298 K: (a) experimental data and (b) fitted isotherm model data.
1, 5 M NaOH) at pH 6 and 298 K: (a) experimental data and (b) fitted isotherm model data.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, T = 298 K)
1, 5 M NaOH) (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, T = 298 K)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH)
1, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), achieving an R2 value of 0.998. Furthermore, other variants, such as BFO (1
1, 5 M NaOH), achieving an R2 value of 0.998. Furthermore, other variants, such as BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH), BFO (2
2, 5 M NaOH), BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), and BFO (1
1, 5 M NaOH), and BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH), also displayed good fits with the PSO model, whereas BFO (1
1, 8 M NaOH), also displayed good fits with the PSO model, whereas BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH) aligned better with the PFO model based on their respective R2 values. Notably, the qe values calculated from the PSO model closely matched the experimental qe values. Hence, the PSO model emerged as the most accurate in predicting the adsorption kinetics of TCS onto BFO materials.
1, 3 M NaOH) aligned better with the PFO model based on their respective R2 values. Notably, the qe values calculated from the PSO model closely matched the experimental qe values. Hence, the PSO model emerged as the most accurate in predicting the adsorption kinetics of TCS onto BFO materials.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH)
1, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH)
2, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH)
1, 5 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH)
1, 3 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH)
1, 8 M NaOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity, and the average kinetic data were plotted (Fig. 11) till the equilibrium time of 180 minutes. The fitted kinetic data for PFO and PSO are shown in Table 5.
1, 5 M NaOH). Consequently, the adsorption experiment was replicated three times to acquire an average adsorption capacity, and the average kinetic data were plotted (Fig. 11) till the equilibrium time of 180 minutes. The fitted kinetic data for PFO and PSO are shown in Table 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) at pH 6 and 298 K: (a) experimental kinetic data and (b) kinetic fitting data.
1, 5 M NaOH) at pH 6 and 298 K: (a) experimental kinetic data and (b) kinetic fitting data.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) sample (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, pH = 6, T = 298 K)
1, 5 M NaOH) sample (C0 = 200 mg L−1, adsorbent loading = 0.2 g L−1, pH = 6, T = 298 K)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH)
1, 5 M NaOH)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH).
1, 5 M NaOH).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) from 903 mg g−1 to 764 mg g−1. In general, elevated pH levels can lead to increased ionization, causing the surface functional groups to become partially or fully deprotonated, consequently resulting in the accumulation of negative charges.39 As a result, alterations in solution pH affect the dissociation of TCS molecules. It is worth noting that TCS (with a pKa of 8.14) doesn't dissociate at acidic pH levels. It exists in a molecular (non-dissociate) state at pH less than its pKa and in anionic form at pH greater than the pKa.11 This lack of dissociation at acidic pH reduces electrostatic repulsive interactions, consequently boosting the adsorption capacity. The impact of pH on the adsorption of organic chemicals hinges on various forces, such as electron donor–acceptor (EDA) interactions, charge repulsion, and specific attractive forces like hydrogen bonding and hydrophobic interactions. Thus, the effect of pH on TCS adsorption can be explained by investigating the solution pH, TCS pKa, and the pHpzc of BFO.
1, 5 M NaOH) from 903 mg g−1 to 764 mg g−1. In general, elevated pH levels can lead to increased ionization, causing the surface functional groups to become partially or fully deprotonated, consequently resulting in the accumulation of negative charges.39 As a result, alterations in solution pH affect the dissociation of TCS molecules. It is worth noting that TCS (with a pKa of 8.14) doesn't dissociate at acidic pH levels. It exists in a molecular (non-dissociate) state at pH less than its pKa and in anionic form at pH greater than the pKa.11 This lack of dissociation at acidic pH reduces electrostatic repulsive interactions, consequently boosting the adsorption capacity. The impact of pH on the adsorption of organic chemicals hinges on various forces, such as electron donor–acceptor (EDA) interactions, charge repulsion, and specific attractive forces like hydrogen bonding and hydrophobic interactions. Thus, the effect of pH on TCS adsorption can be explained by investigating the solution pH, TCS pKa, and the pHpzc of BFO.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) was found to be 8.5 by measuring its zeta potential across various pH values (3, 6, 7, and 9), as illustrated in Fig. 12(c). The surface of BFO is positively charged when pH < 8.5, while it will be negatively charged at pH > 8.5. When adsorption occurs at a pH level below 8.14 (pH < pKa < pHpzc), the solution predominantly contains TCS in its non-dissociated form, while BFO exhibits a positive surface charge. This scenario results in improved adsorption capacity owing to increased attractive interactions, such as hydrogen bonding and hydrophobic interactions, coupled with reduced repulsive electrostatic interactions. In contrast, at pH > pKa, TCS in the solution is in its anionic state, aligning with the negative charge present on the surface of BFO (pH > pHpzc). As a result, electrostatic repulsion opposes attractive interactions, ultimately contributing to a decline in the adsorption capacity of TCS with increasing pH levels.
1, 5 M NaOH) was found to be 8.5 by measuring its zeta potential across various pH values (3, 6, 7, and 9), as illustrated in Fig. 12(c). The surface of BFO is positively charged when pH < 8.5, while it will be negatively charged at pH > 8.5. When adsorption occurs at a pH level below 8.14 (pH < pKa < pHpzc), the solution predominantly contains TCS in its non-dissociated form, while BFO exhibits a positive surface charge. This scenario results in improved adsorption capacity owing to increased attractive interactions, such as hydrogen bonding and hydrophobic interactions, coupled with reduced repulsive electrostatic interactions. In contrast, at pH > pKa, TCS in the solution is in its anionic state, aligning with the negative charge present on the surface of BFO (pH > pHpzc). As a result, electrostatic repulsion opposes attractive interactions, ultimately contributing to a decline in the adsorption capacity of TCS with increasing pH levels.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5M NaOH).
1, 5M NaOH).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5M NaOH) with the reported adsorbents in literature
1, 5M NaOH) with the reported adsorbents in literature

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), TCS and TCS absorbed BFO (BFO + TCS), whereas Fig. 13(b) shows the FTIR spectra of fresh and washed BFO after adsorption. For fresh BFO (1
1, 5 M NaOH), TCS and TCS absorbed BFO (BFO + TCS), whereas Fig. 13(b) shows the FTIR spectra of fresh and washed BFO after adsorption. For fresh BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH), the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33,46,47
1, 5 M NaOH), the absorption bands at around 803 cm−1 and 609 cm−1 in the infrared spectrum are typically attributed to Fe–O stretching and Fe–O–Fe bending vibrations within the FeO4 tetrahedron, respectively32,33 The absorption bands at around 486 cm−1, 454 cm−1 and 426 cm−1 are assigned to the Fe–O stretching vibration and bond stretching in the FeO6 octahedron.33,46,47
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8 M NaOH) > BFO (1
1, 8 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 5 M NaOH) > BFO (2
2, 5 M NaOH) > BFO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5 M NaOH) > BFO (1
1, 5 M NaOH) > BFO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3 M NaOH). The kinetic analysis revealed the second-order kinetic model to be the best fit for these BFO materials. The adsorption–desorption equilibrium was achieved within 180 minutes, and the Redlich–Peterson model properly described the adsorption isotherms of TCS on BFO. The mean free adsorption energy obtained from the D–R isotherm suggests that the adsorption process in BFO materials involves physical adsorption mechanisms, predominantly hydrogen bonding and electrostatic interactions. The study of pH effects showed that at a lower pH of 3, the interaction between TCS and BFO was enhanced, leading to improved adsorption capacity. Moreover, it was found that lower adsorbent loadings result in higher adsorption capacities. This is attributed to the overlapping of adsorption sites at higher adsorbent loadings, which reduces adsorption effectiveness. The BFO sample with a 1
1, 3 M NaOH). The kinetic analysis revealed the second-order kinetic model to be the best fit for these BFO materials. The adsorption–desorption equilibrium was achieved within 180 minutes, and the Redlich–Peterson model properly described the adsorption isotherms of TCS on BFO. The mean free adsorption energy obtained from the D–R isotherm suggests that the adsorption process in BFO materials involves physical adsorption mechanisms, predominantly hydrogen bonding and electrostatic interactions. The study of pH effects showed that at a lower pH of 3, the interaction between TCS and BFO was enhanced, leading to improved adsorption capacity. Moreover, it was found that lower adsorbent loadings result in higher adsorption capacities. This is attributed to the overlapping of adsorption sites at higher adsorbent loadings, which reduces adsorption effectiveness. The BFO sample with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi/Fe mole ratio and 5 M NaOH concentration exhibited the highest TCS adsorption capacity of 903 mg g−1 at pH 3, with an adsorbent loading of 0.2 g L−1 at a temperature of 298 K. In summary, BFO nanosheets exhibit excellent adsorption capacity toward triclosan, attributed to their active surface sites and nanosheet morphology. These results demonstrate that BFO nanosheets are a promising and environmentally sustainable material for the efficient removal of emerging contaminants from wastewater.
1 Bi/Fe mole ratio and 5 M NaOH concentration exhibited the highest TCS adsorption capacity of 903 mg g−1 at pH 3, with an adsorbent loading of 0.2 g L−1 at a temperature of 298 K. In summary, BFO nanosheets exhibit excellent adsorption capacity toward triclosan, attributed to their active surface sites and nanosheet morphology. These results demonstrate that BFO nanosheets are a promising and environmentally sustainable material for the efficient removal of emerging contaminants from wastewater.






