Droplet electrocoalescence as a robust tool for in situ examination of hydrogel microparticles in microfluidic devices
Andrei
Tiushkevich
 a,
Nikita
Filatov
a,
Pavel
Pleshakov
a and
Anton
Bukatin
a,
Nikita
Filatov
a,
Pavel
Pleshakov
a and
Anton
Bukatin
 *ab
*ab
aAlferov Saint Petersburg National Research Academic University of the Russian Academy of Sciences, Khlopina St., 8-3, lit. A, St. Petersburg 194021, Russia. E-mail: antbuk.fiztek@gmail.com
bInstitute for Analytical Instrumentation of the Russian Academy of Sciences, St. Ivana Chernykh, 31-33, lit. A, St. Petersburg 198095, Russia
First published on 3rd December 2025
Abstract
Nowadays hydrogel microparticles find numerous applications in material science and biological engineering such as drug delivery systems, cell carriers, etc. Droplet microfluidics provides an efficient tool for producing monodisperse microparticles, however, optimization of synthesis conditions remains challenging. Here, we developed a simple and easy-to-use method for in situ visual assessment or quantitative characterization of hydrogel crosslinking inside water-in-oil droplets. It is based on the difference in the merging dynamics of water-in-oil emulsions and crosslinked hydrogel microparticles in an external electric field and is compatible with various designs of microfluidic devices, types of materials and crosslinking mechanisms. Integrating a metal electrode into a microfluidic device with a flow-focusing droplet generator, we investigated how water-in-oil droplet merging occurs and then demonstrated that electrocoalescence can be used for in situ characterization of the polyacrylamide, polyethylene glycol diacrylate and alginate microparticles during their crosslinking. We suggest that implementation of the droplet electrocoalescence for in situ control of hydrogel crosslinking technique paves the way to achieve efficient, stable and reproducible synthesis of hydrogel microparticles, which is highly demanded for biomedical applications.
1 Introduction
Currently, microparticles (MPs) in the size range from 0.1 to 100 micrometers are widely used in pharmaceuticals, food industry, cosmetology, photonics, industrial coating, and biofabrication.1–5 Recent developments can be clearly seen in the biomedical field, where MPs are used as cell containers for drug delivery, scaffold building and tissue engineering, as well as identifiers and actuators.2 Encapsulation of active substances (e.g., proteins/cells) into such MPs opens the way for many application scenarios, such as high-throughput biological assays,6–8 tissue regeneration, assembling of artificial tissues and organs, 3D bioprinting, etc.9–11 All this has become possible thanks to the ability to design and ensure MPs' size, structure and composition during fabrication, which significantly increases their functionality.However, the straightforward generation of MPs of a given size in a stable and highly controlled manner remains challenging. Precise control over MP size distribution, compartment dimensions, and the number of encapsulated cells is critical, as intercellular spacing and structural arrangement significantly influence cellular properties and functions.12 Well-known conventional methods, such as emulsion polymerization, dispersion polymerization and spray drying do not allow the formation of monodisperse MPs with high reproducibility, diverse morphologies and high levels of compartmentalization.13 To overcome these obstacles, a variety of techniques, such as droplet microfluidics, flow lithography microfluidics, electrohydrodynamic co-jetting, photolithography, and soft lithography-based imprinting and micromolding, have been recently developed to produce different types of monodisperse MPs.14–16
Among others, droplet microfluidics is one of the most promising technologies for generation of monodisperse MPs.17–19 It allows creating and manipulating discrete volumes of liquids in immiscible phases of laminar flows, providing precisely tunable morphology of MPs with high performance, suitable for medical, pharmaceutical and cosmetic industry.20–24 However, the usage of droplet microfluidics for the MPs production has its own challenges. Since water-in-oil (W/O) droplets themselves cannot be in thermodynamic equilibrium, emulsion stabilization during the synthesis becomes an important issue.25–27 For many biological applications, the choice of surfactants is limited by cytotoxicity concerns.28 All this makes the adjustment of the synthesis parameters challenging, requiring a reliable and easy-to-use method for in situ control of physicochemical properties, morphology and structure of MPs during their synthesis.
Various methods have been proposed to anticipate hydrogel MPs properties and behavior.29 For example, optical and confocal microscopy are used to study morphology and internal structure of individual MPs. A more detailed analysis of the hydrogel structure including pores diameter is provided by scanning or transmission electron microscopy.30 Atomic force microscopy and optical spectroscopy, such as FTIR or Raman, together with thermal analysis techniques, such as thermogravimetric analysis (TGA) or differential scanning calorimetry (DSC), are used to determine mechanical properties, chemical structure and thermal stability of the obtained MPs.31–33 Despite the undeniable advantages of these methods they require a multi-step sample preparation process, are time-consuming and complicated for the analysis. Therefore, they hardly can be used for in situ monitoring of MPs characteristics and track their properties changes during the synthesis.
For the microfluidic synthesis of MPs, various methods enable precise in situ analysis of droplet ensembles and single microgel particles.34–36 Mechanical properties of these microgel are frequently characterized by analyzing the deformation of individual MPs under shear flow.37,38 Alternatively, an electric field is a promising tool for colloids manipulation, which began long before microfluidics.39–41 For example, electrocoalescence of emulsions is widely used in the oil industry for dehydration and desalting of crude oil.42 In droplet microfluidics, external electric fields were introduced for highly efficient droplet manipulation, e.g., reagent addition for multistep reactions inside droplets,43,44 rapid mixing of highly reactive materials,45 droplet content recovery46,47 and high-throughput fluorescence activated droplet sorting for single cell analysis48–50 and single cell amplification and sequencing.8
Electrocoalescence phenomena consists in the ability of liquid droplets to attract and merge with each other in an external electric field. According to the previous studies, this process can be divided into 4 stages: approach, reconnection, coalescence and merging.51 Polarized droplets migrate in the electric field due to dielectrophoresis, which is determined by dielectric constants of droplets and surrounding media.52 Changes in viscoelastic properties of hydrogel materials during their crosslinking can alter coalescence dynamics at the approach and merging stages.51,53,54 The presence of hydrogel network can alter the dielectric constant of droplets depending on sol/gel solution condition.55,56 Moreover, the crosslinked hydrogel provides extra friction with glass surfaces, which can lead to the decrease of the MPs velocity and increase the duration of the approach stage.57,58 During the merging stage, material reflows between connected droplets to form a larger, unified droplet. However, the evolving viscoelastic properties of the hydrogel impede this reflow, leading to incomplete MPs merging.53 Since these viscoelastic properties directly affect both the droplet approach velocity and the internal material reflow during electrocoalescence, it provides a useful metric for in situ examination of the hydrogel's polymerization degree.
Here, we present a novel method for in situ characterization of hydrogel MPs produced by droplet microfluidics. The method is based on the difference of the electrocoalescence dynamics of W/O emulsions and crosslinked hydrogel MPs in an external high-voltage electric field. Integrating a metal electrode into a microfluidic device with a flow-focusing droplet generator, we investigated W/O droplets merging dynamics and then demonstrated that electrocoalescence can be used for in situ examination of the polyacrylamide (pAAm), polyethylene glycol diacrylate (PEGDA) and alginate MPs after their crosslinking. The method proved to be quite universal and compatible with different configurations and sizes of microchannels, and two types of hydrogel crosslinking processes, such as ultraviolet (UV) exposure and interfacial polymerization. Applying our method to PEGDA MPs, we figured out that the crosslinking process depends on the size of the microchannel and the droplet size due to crosslinking inhibition by atmospheric oxygen, diffused into the droplets through PDMS.
2 Materials and methods
2.1 Design of the microfluidic devices
To investigate the influence of external electric fields on liquid emulsion and hydrogel MPs, a microfluidic device with a W/O emulsion generator was used (SI, Fig. S1). The microfluidic device consists of two functional sections: a flow-focusing droplet generator and a rectangular outlet channel, as shown in Fig. 1. The droplet generator has a 15 µm aperture and can produce monodisperse droplets from 35 to 120 µm in diameters at frequencies from 15 to 100 Hz. The height of the channels is 45 µm, except the outlet channel, which height was increased to 80 µm to prevent MPs from clogging. The length of the outlet channel is 37 mm, while its width is 1 mm. The other versions of the device have different outlet channels, which width, wchannel, is 0.1 mm and 10 mm. Droplet travelling time in a 1 mm wide channel was between 90 to 200 seconds depending on the liquids flow rates.To induce droplets electrocoalescence in the microfluidic device, it is necessary to locally apply an electric field in the outlet channel with the field strength 2–10 kV cm−1.59–61 To generate such field, we made an aluminum electrode from a 1 mm wide strip of aluminum tape attached to the bottom side of the microfluidic device and connected it to a low-power high-voltage radio frequency oscillator, from a portable medical device for high frequency electrotherapy (Karat, DE-212). Its electric scheme is presented in Fig. S2 in SI. The oscillator is similar to a Tesla coil and is capable of producing voltage oscillations ranging from 2 to 9 kV, with a pulse packet repetition rate of 100 ± 10 Hz and a pulse filling frequency of 100 ± 25 kHz. The advantage of using such electrode is simple fabrication and applicability to any kind of PDMS microfluidic device where a 0.17 mm microscope cover glass or a PDMS film of similar thickness is used as the bottom side of the device. The reference electrode in the device is coupled via a capacitor to the neutral phase of the power supply, so the ground is virtually located at an infinite distance from the microfluidic device and doesn't require the second electrode.
2.2 Fabrication of microfluidic devices
To fabricate microfluidic devices from polydimethylsiloxane (PDMS, Sylgard 184, Dow Silicones, Midland, MI, USA), a standard soft lithography technique was used.62,63 Briefly, the mold was fabricated by a two-step contact photolithography with a chromium mask on a silicon wafer covered with SU-8 2025 layers (Kayaku Advanced Materials, West borough, MA, USA). Then PDMS mixture, containing prepolymer and the curing agent in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio by weight, was thoroughly mixed, degassed, and poured onto the mold. After curing in an oven at 65 °C for 4 hours, the PDMS replica was separated from the mold and cut into individual devices. Inlet and outlet holes were made using a 2 mm biopsy puncher. Oxygen plasma treatment was used to bond the PDMS replica with a 24 × 60 mm microscope cover glass (thickness 0.17 mm). An anti-rain reagent (Turtle Wax, Addison, IL, USA) was used to create a hydrophobic coating on the inner walls of the microchannels achieving a contact angle of 100°.
1 ratio by weight, was thoroughly mixed, degassed, and poured onto the mold. After curing in an oven at 65 °C for 4 hours, the PDMS replica was separated from the mold and cut into individual devices. Inlet and outlet holes were made using a 2 mm biopsy puncher. Oxygen plasma treatment was used to bond the PDMS replica with a 24 × 60 mm microscope cover glass (thickness 0.17 mm). An anti-rain reagent (Turtle Wax, Addison, IL, USA) was used to create a hydrophobic coating on the inner walls of the microchannels achieving a contact angle of 100°.
2.3 Materials for emulsion generation and MPs synthesis
Light mineral oil (Sigma-Aldrich, USA, cat. No 330779) with a 3.5 wt% Abil EM 180 surfactant (Evonik Industries AG, Essen Germany) was used as the continuous liquid phase for droplet generation. Oil viscosity measured by the SV-10 Viscometer, 0.3 cP–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cP (A&D, Japan), is presented in Fig. S3A. The surfactant stabilizes emulsions decreasing the interfacial surface tension of water–oil interface from 13.3 mN m−1 to 5.5–7.5 mN m−1 in the range of concentrations 2–9 wt% (SI, Fig. S3B). Such changes of interfacial surface tension are relatively small to affect the dynamics of electrocoalescence, therefore it doesn't depend on small variations of the surfactant concentration in the investigated range.51
000 cP (A&D, Japan), is presented in Fig. S3A. The surfactant stabilizes emulsions decreasing the interfacial surface tension of water–oil interface from 13.3 mN m−1 to 5.5–7.5 mN m−1 in the range of concentrations 2–9 wt% (SI, Fig. S3B). Such changes of interfacial surface tension are relatively small to affect the dynamics of electrocoalescence, therefore it doesn't depend on small variations of the surfactant concentration in the investigated range.51
Three aqueous solutions of monomers were used as the dispersed phase for MPs synthesis. For polyacrylamide (pAAm) MPs aqueous (Millipore Milli-Q) solution of 30% acrylamide/bis solution 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Bio-Rad, USA, cat. No 1610156) with a final concentration of 10 vol%, ammonium persulfate (APS, Sigma-Aldrich, USA, cat. No A3678) with a concentration of 0.3 to 1.5 wt% was used. Polyethylene glycol diacrylate (PEGDA) (Sigma-Aldrich, USA, cat. No 455008) aqueous solution with a concentration of 30 to 70 wt% and a photoinitiator 2 hydroxy-4-(2-hydroxyethoxy)-2-methylpropiopiophenone (Irgacure 2959, Sigma-Aldrich, USA, cat. No 410896) with a concentration of 0.5 to 10 wt% was used for MPs production as well. For alginate MPs an aqueous solution of alginate (Sigma-Aldrich, USA, cat. No W201502) with a concentration of 1.7 wt% and Ca–EDTA, (Sigma-Aldrich, USA, cat. No ED2SC) with a concentration of 10 wt% was used. Additionally, for alginate MPs 100% acetic acid was added to the continuous phase to achieve final concentration of 1.5 vol% to release calcium ions from the Ca–EDTA complex after droplet formation and induce alginate crosslinking.64 In case of pAAm MPs synthesis N,N,N′,N′-tetramethylethylenediamine (TEMED, Sigma-Aldrich, USA, cat. No T9281) at a concentration of 1.5 vol% was added to the continuous phase. After the droplet formation it diffuses into the droplets and catalyzes pAAm crosslinking.
1 (Bio-Rad, USA, cat. No 1610156) with a final concentration of 10 vol%, ammonium persulfate (APS, Sigma-Aldrich, USA, cat. No A3678) with a concentration of 0.3 to 1.5 wt% was used. Polyethylene glycol diacrylate (PEGDA) (Sigma-Aldrich, USA, cat. No 455008) aqueous solution with a concentration of 30 to 70 wt% and a photoinitiator 2 hydroxy-4-(2-hydroxyethoxy)-2-methylpropiopiophenone (Irgacure 2959, Sigma-Aldrich, USA, cat. No 410896) with a concentration of 0.5 to 10 wt% was used for MPs production as well. For alginate MPs an aqueous solution of alginate (Sigma-Aldrich, USA, cat. No W201502) with a concentration of 1.7 wt% and Ca–EDTA, (Sigma-Aldrich, USA, cat. No ED2SC) with a concentration of 10 wt% was used. Additionally, for alginate MPs 100% acetic acid was added to the continuous phase to achieve final concentration of 1.5 vol% to release calcium ions from the Ca–EDTA complex after droplet formation and induce alginate crosslinking.64 In case of pAAm MPs synthesis N,N,N′,N′-tetramethylethylenediamine (TEMED, Sigma-Aldrich, USA, cat. No T9281) at a concentration of 1.5 vol% was added to the continuous phase. After the droplet formation it diffuses into the droplets and catalyzes pAAm crosslinking.
2.4 Experimental setup
The liquids were injected into the microfluidic device under constant pressures using a custom microfluidic pressure controller.65 An inverted optical microscope (Axiovert 200, Zeiss, Oberkochen, Germany) with a camera (Daheng Imaging, Beijing, China) with a 100 frames per seconds regime was used to observe the droplets and MPs behavior. For PEGDA crosslinking a 10 W UV diode with a wavelength of 365 nm and lighting power density of 60 mW cm−2 was used. To reduce the polymerization time of pAAm MPs, the microfluidic device was partly placed on an indium tin oxide (ITO) coated glass slide maintaining the temperature of up to 50 °C. The part of the microfluidic device with the droplet generator was cooled to a room temperature by a custom-made water-cooled radiator. For experiments with PEGDA MPs, oil degassing took place in a desiccator at a pressure of −70 kPa for 4 hours. The recording of the droplet electrocoalescence was captured in an observation area, which was a rectangular section with a side of 1 mm (Fig. 1). The distance between the nearest edge of the electrode and the center of the observation area, ldistance varied from 0.5 to 10 mm. When the ldistance value was 0.5 mm, the electrode touched the border of the observation area.2.5 Data analysis
Droplet sizes were calculated by analyzing bright-field microscopic images with a custom script, developed using Python 3.9 and the OpenCV program package. The image processing was based on a cv2.HoughCircle function for circles detection on imperfect images.66 Further details are presented in SI: visualization of the droplet detection is shown in Fig. S4; the droplets size distributions are shown in Fig. S5 and Table S1. All the graphs were prepared with “seaborn” python library and present the average values and standard deviation from at least three experiments conducted under the same experimental conditions.3 Results and discussion
3.1 Electrocoalescence of water-in-oil droplets
Initially, we performed the electrocoalescence of W/O droplets in microfluidic channels to figure out how merging dynamics depend on various parameters. To achieve this, we generated monodispersed droplets in the microfluidic device, filled the outlet channel with them and ceased the inlet flows to stop the droplets movement. After the flow stopped completely, we applied a 2 kV peak voltage oscillation to the electrode, located at a 0.5 mm distance from an observation area, which caused the electrocoalescence, as shown in Fig. 2. The droplets merging occurred in all the channels regardless of their width. Due to the camera's temporary resolution of 0.01 s, the dynamics of two out of four coalescence stages (approach and merging) were visually observed.51 The image sequence, presented in Fig. 2A, demonstrates that the closely located droplets merged during the first 0.05 s (Video S1). The electric field then attracted more distant droplets to each other, causing them to merge. The whole process ended in 5 s. Thus, the main result of the W/O droplet electrocoalescence is the formation of bigger droplets of different sizes randomly distributed in the microfluidic channel. Because of the large distance between them, the applied electric field was not strong enough to attract and merge all the droplets into a single one. This result indicates that the initial distance between droplets is a key parameter for the electrocoalescence dynamics.Performing electrocoalescence in a fluid flow regime, we should take into account the fact that the laminar two-phase flow of W/O droplets is a non-equilibrium many-body phenomenon.67 The movement of droplets is influenced by the mutual hydrodynamic dipole–dipole interaction.35 The distance between the droplets in a fluid flow has large variations due to a peloton effect,68,69 making it difficult to analyze the electrocoalescence dynamics. To address this, we calculated the droplet density per area, ρarea, and average distance between the nearest droplets, κ:
 | (1) |
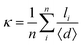 | (2) |
At different flow regimes, droplets concentration may vary significantly depending on the chosen observation area and travelling time in the outlet channel. To investigate this and figure out an optimal place for performing droplet coalescence to obtain robust results, we calculated ρarea and κ along the outlet channel (Fig. 3). According to the obtained results, the droplets behavior in the 2D flow follows the Taylor's distribution.70 We described the emulsion flow based on the average concentration of droplets in the 1 × 1 mm2 observation area, located at the beginning of the channel. Further, we inspected the flows, where the range of average droplet densities varied from 0.15 to 0.42. At the travelling distances in the outlet channel of 0 to 3–7 mm, depending on the flow rates, the droplets are grouped close to each other near the center of the channel with the average separation distance, κ, close to 1. Further down the channel, the droplets were dispersing over the whole channel's width, which led to increasing the average distance between the droplets accompanied by significant fluctuations in the values of ρarea and κ. Ultimately, after ∼30 mm channel length, the droplets spread evenly over the entire channel, and the fluctuations of ρarea and κ were reduced. The droplets arrived in the most energy-efficient state of the W/O system with the lowest droplet interaction with each other and maximum average κ values. Therefore, we chose the location of the electrode and the observation area for the electrocoalescence experiments near the end of the outlet channel, as shown in Fig. 1, where the droplet behavior is stable and predictable. Additionally, for detail characterization of each electrocoalescence event, we began to calculate the average values of ρarea and κ in the area within 0.05 seconds before switching on the electric field.
 | ||
| Fig. 3 Characterization of the droplet flow in the 1 mm-wide outlet channel. (A) Optical images of the droplet flow captured 0.5 mm from the beginning of the channel, representing five different average droplets concentrations, 〈ρarea〉. (B)–(D) Spatial evolution of droplet concentration (ρarea, dot color) and average mutual distance (κ, dot position) along the channel axis. Each data point was calculated from a single image taken at 5 s intervals at fixed axial positions. The datasets correspond to the average inlet concentrations shown in (A): (B) 〈ρarea〉 = 0.15, (C) 0.25, and (D) 0.42. The black curve represents a locally weighted linear regression (LOWESS) on κ.71 The scale bar is 150 µm. | ||
Characterization of the W/O droplet flow by ρarea, κ, and 〈ddroplet〉 allowed us to investigate the electrocoalescence dynamics in certain flow conditions. To quantify the process, we calculated the relative number of droplets in the observation area in the outlet channel, Nt/N0. Nt is defined as the quantity of droplets in the observation area by time t, and N0 is the quantity of droplets in the observation area prior to the supplying of voltage to the electrode. When the electric field was turned on, the number of droplets exponentially decreased with the time constant 0.07–0.1 s, which did not depend on the droplet concentration, ρarea, (Fig. 4A). However, the total number of merged droplets 1 − Nt/N0 increased with increasing the average concentration, 〈ρarea〉, and decreasing the average inter-droplet distance, κ, (Videos S2 and S3). To evaluate the robustness of this process and its sensitivity to device-to-device variations, we repeated the experiment across three separate microfluidic devices of the same design, with nine replicates per device (SI, Fig. S6). The process showed consistent performance, with an average coefficient of variation (CV) of 10% at a high droplet concentration (〈ρarea〉 = 0.51) and 8% at a lower concentration (〈ρarea〉 = 0.34). These low CV values demonstrate that droplet merging dynamics are not significantly affected by inherent variations in the fabrication of microfluidic devices with this design.
Similarly, we measured the merging dynamics at different temperatures of the microfluidic device (Fig. 4B). At 20 °C, droplet merging is hindered by medium viscosity, which generates a Stokes friction force (Video S4). At a higher temperature, the viscosity of the continuous phase is halved (SI, Fig. S3A), reducing the Stokes force. This reduction leads to stronger droplet attraction and more frequent merging (Video S5). Consequently, the distance of effective merging in the same electric field becomes larger, which results in inverse proportionality between the final number of droplets after the electrocoalescence and the temperature of the microfluidic device.
The electric field strength is another key parameter that influences droplet coalescence dynamics. According to the COMSOL electric field simulations (SI, Fig. S7), it is mainly affected by the distance from the droplets in the observation area to the electrode, ldistance, and the applied voltage. The presence and magnitude of the exponential decay of the number of droplets in the observation area strongly depended on the distance to the electrode, ldistance, (Fig. 5A) and on the droplet density, 〈ρarea〉, (Fig. 5B). At a distance of 0.5 mm, about 60% of the droplets merged in a time scale of 0.1 s. When the distance was 5 mm, about 25% of droplets coalesced in the first 0.1 s. After further droplets merging during the next 2.9 s, caused by mutual approaching, the total number of droplets decreased to 25% from the initial number. At a distance of 10 mm, only 7.5% of droplets coalesced in the first 0.1 s and 40% by the time of observation. In addition, the data on Fig. 5B shows that the influence of the distance to the electrode on the electrocoalescence dynamics is more pronounced at lower droplet densities. When half of the channel's area is occupied by droplets (ρarea = 0.49), increasing the distance to the electrode from 5 to 10 mm does not lead to significant changes in droplet merging dynamics. But when only one third of the channel's area is occupied by droplets (ρarea = 0.36), these changes are dramatic.
Thus, we can describe droplet flow by, 〈ρarea〉, 〈κ〉, and 〈daverage〉, and control the intensity of the electrocoalescence by changing the continuous phase viscosity and electric field strength, determined by the distance between the electrode and the observation area. The relative number of droplets Nt/N0 in the channel calculated under particular flow regime can be a robust parameter describing the electrocoalescence dynamics of W/O emulsions in a two-phase flow in a microfluidic channel.
3.2 Electrocoalescence of hydrogel-in-oil emulsions
After investigating the electrocoalescence dynamics of W/O emulsions in microfluidic channels, we switched to the investigation of the hydrogel-in-oil emulsions electrocoalescence in the same microfluidic channels and similar conditions. The viscoelastic properties of MPs change qualitatively within distinct timeframes: alginate within milliseconds via Ca+2 crosslinking by chelation, PEGDA within 1–5 s via UV polymerization, and pAAm within 2 minutes via radical polymerization, as previous studies have shown.72–77 Since our observations began after a 3-minute transit time, we expected all MPs to have fully crosslinked and achieved viscoelastic stability. Quantifying the viscoelastic changes in the resulting MPs is challenging, as conventional rheological methods are ill-suited for measuring individual microparticles, and effective interparticle interactions further complicate the analysis.29,30,78–80 However, the system's behavior can be understood by approximating it as a bulk solution, where the sol–gel transition significantly increases the overall viscosity (η, Pa s) and elastic modulus (G′, Pa).81 Indeed, at a fixed shear rate of 100 s−1—chosen to match the rate of droplet electrocoalescence—the viscosity of crosslinked alginate, pAAm, and PEGDA increases by a factor of 10 to 100 after crosslinking.77,82,83Initially, we studied the behavior of pAAm, alginate and PEGDA hydrogel microparticles (MPs) after 24 h storage in crosslinking conditions to be sure that the hydrogels were fully crosslinked. Optical microscopy showed that fully crosslinked PEGDA particles could be distinguished from liquid droplets on the images, while pAAm and alginate particles looked the same as liquid droplets (Fig. 6). Moreover, all the fully crosslinked particles did not respond to the electric field. This can be explained by the changes of viscoelastic properties of the hydrogels after crosslinking, which prevents droplets attraction and merging.51,53,54 Therefore, the difference in droplets and MPs behavior in the external electric field can serve as an indicator of the degree of hydrogel crosslinking inside the W/O droplets.
Similar to the electrocoalescence of aqueous droplets, we quantitatively measured the relative number of droplets, Nt/N0, during the electrocoalescence of alginate MPs in the 1 mm wide outlet channel of the microfluidic device (Fig. 7). Acetic acid diffused from the continuous phase into the droplets and initiated alginate crosslinking. Therefore, we observed that the droplets' merging dynamics dramatically depended on its concentration in the continuous phase. In a control experiment, when no acetic acid was added, the electrocoalescence of alginate droplets had a time scale of the initial exponential decay of 0.9 s. Adding 0.12 wt% of acetic acid into the continuous phase led to a decrease in the number of merged droplets increasing the time scale of the process. When the concentration of acetic acid was increased up to 1 wt%, the droplets' merging did not occur, which indicated the high degree of alginate crosslinking inside the droplets. However, careful examination of the images shows that some droplets in the electric field were combined into clusters with solid cores and single liquid shell. This indicates that in our experimental conditions, the droplets traveling time in the outlet channel (3 min) is not enough for full crosslinking of alginate.
We performed electrocoalescence of pAAm droplets at the same flow conditions as the alginate ones, except the temperature of the outlet channel was increased to 38 °C; the results are shown in Fig. 8. When the cross-linking initiator APS and the catalyst TEMED were added into the dispersed and the continuous phases respectfully, we observed decrease of the droplets merging events during the first 3 second, compared to the control experiment. However, in the electric field pAAm droplets combined into several clusters with multiple hydrogel cores and single liquid shell. Such behavior indicates that the droplets travelling time to the end of the outlet channel is not enough to fully crosslink the hydrogel inside the droplets.
3.3 Investigation of PEGDA crosslinking in microgels
In case of alginate and pAAm hydrogels their crosslinking inside W/O droplets cannot be noticed by optical microscopy (Fig. 6), conducting verification of the hydrogel crosslinking quite difficult. Surprisingly, PEGDA crosslinking led to the formation of hydrogel cores inside W/O droplets, which could be visually observed in a bright-field optical microscope. Therefore, we investigated electrocoalescence of PEGDA MPs in the microfluidic device in more detail.PEGDA droplets behavior in the electric field without crosslinking by UV radiation (control experiment) was similar to the W/O emulsion (Fig. 9, blue curve). We observed the initial exponential decay with timescale of 0.1 s in both cases of the presence and absence of UV exposure. However, further droplet merging occurred only in control experiments. Such a significant difference in droplet merging dynamics occurred due to the formation of hydrogel cores from fully crosslinked PEGDA, which occurred during 3 minutes of UV illumination. These cores did not merge with each other but combined into clusters with shared liquid shells. Such clusters can be separated into individual particles by vortexing.
According to the merging dynamics of PEGDA MPs after 3 min UV exposure, PEGDA starts crosslinking from the droplet center, forming a polymer core. However, the efficiency of this process depends on oxygen concentration inside the droplets, as oxygen can inhibit the crosslinking reaction.76,77,84 In the developed microfluidic device, due to high gas-permeability of PDMS, atmospheric oxygen can diffuse inside the droplets and terminate the growth of the polymer chains. One of the ways of dealing with the atmospheric oxygen in PDMS microfluidic devices is to put them into inert, for example nitrogen, environment.76 Nevertheless, under normal environment, even relatively small MPs can have cores that are surrounded by a liquid shell of unpolymerized solution. Analyzing PEGDA MPs of different diameters, we observed that the thickness of the liquid shell layer in individual droplets after hydrogel crosslinking has a slight dependence on the diameter of the droplets, as shown in Fig. 10A, which is in agreement with the previous studies.76,77
Performing PEGDA MPs synthesis in the microfluidic device with 1 mm wide outlet channel, we noticed that hydrogel cores in droplets, located in the middle of the flow, were bigger than in those located near the sidewalls of the channel, as shown in Fig. 10B. To understand this phenomenon, we performed a COMSOL simulation of the oxygen concentration distribution during the photopolymerization process and found that the droplet concentration did not significantly affect the oxygen profile in the channel (SI, Fig. S8). Then, we assumed that such difference in PEGDA crosslinking can be caused by the diffusion length of oxygen molecules in the continuous phase (mineral oil) along the flow. In the case of deoxygenation of the initial oil solution, the oxygen concentration profile in the channel in the observation area has a parabolic profile with a minimum in the center of the channel (SI, Fig. S9). Oxygen concentration is larger near the channel walls causing stronger inhibition of the reaction, which is in good correspondence with our experimental results.
In Fig. 10C, we compiled the diagram that depicts the successful cases of PEGDA hydrogel MPs crosslinking in microfluidic devices with 1 mm and 10 mm wide outlet channels at different concentrations of photoinitiator in the dispersed phase with degassed oil phase. The data obtained in a 0.1 mm wide channel is presented in SI, Fig. S10. PEGDA crosslinking was considered successful if the hydrogel core occupied more than 90% of the droplet volume. Successful synthesis of the smallest MPs with a diameter of 32 µm was achieved only in a 10 mm wide outlet channel, when the concentration of photoinitiator was 0.5 wt%. In a 1 mm and 0.1 mm wide outlet channel, the MPs had diameters from 60 µm and from 75 µm respectively. The data show that the influence of the photoinitiator's concentration in the dispersed phase on the PEGDA crosslinking efficiency is relatively small. However, increasing its concentration from 2 to 4 wt% decreases the minimal droplet diameter with observed hydrogel cores from 80 to 60 µm in a device with a 1 mm wide outlet channel. Thus, our data confirm that the channel's geometry can significantly influence the crosslinking conditions of PEGDA within the W/O emulsions.
4 Conclusions
Here we present a novel easy-to-use method for in situ characterization of hydrogel crosslinking in W/O droplets in microfluidic devices for synthesis of monodispersed hydrogel MPs. It can be used for characterization of hydrogel crosslinking inside droplets by visually assessing or accurately measuring the electrocoalescence dynamics. The method is based on the difference in the merging dynamics of W/O emulsions and crosslinked hydrogel MPs in an external electric field generated by an electrode integrated under the surface of a microfluidic device. The electrode is connected to a low-power high-voltage radio frequency oscillator, similar to a Tesla coil, and can be placed under any part of the device generating electric field in a required area.According to the W/O droplet merging dynamics in microfluidic channels, the timescale of the initial exponential decay of the number of the liquid droplets is 0.1–0.9 s, weakly depending on the experimental conditions and their composition. On the contrary, the further merging dynamics may vary significantly depending on the droplet density, viscosity and temperature of the continuous phase, the distance from the electrode and the composition of droplets. Therefore, comparison of the merging dynamics of liquid droplets and crosslinked hydrogel MPs requires experimental parameters to remain constant.
Experimental results show that the electric field does not affect fully crosslinked alginate, pAAm and PEGDA MPs, which can be explained by the changes in viscoelastic properties of hydrogel materials after crosslinking. This feature can be used for in situ characterization and optimization of the synthesis conditions in a microfluidic device. In the case of alginate droplets their merging dynamics showed that 0.12 wt% of acetic acid in the continuous phase is insufficient, while 1 wt% is almost enough for complete crosslinking of alginate within three minutes during droplet flowing in the outlet channel of the microfluidic device. In the case of alginate and pAAm MPs partial crosslinking, their merging dynamics was significantly different from the same liquid droplets without crosslinking. Due to electrocoalescence they formed clusters with hydrogel cores and shared liquid shells.
Unlike alginate and pAAm, crosslinked PEGDA cores inside the droplets can be visually distinguished from liquid shells. Using this feature, we determined that the liquid shell thickness does not depend on the droplet's diameter, but it depends on the distance to the side walls of the outlet microchannel where UV exposure occurs. The liquid shells are thinner in droplets far away from the side walls. This phenomenon can be explained by atmospheric oxygen diffusion through PDMS into the droplets inhibiting the PEGDA crosslinking reaction. The smallest PEGDA MPs with diameter of 32 µm were obtained only in a microfluidic device with a 10 mm wide outlet channel. In a 1 mm wide outlet channel, MPs with minimal diameter of 60 µm were formed. However, this required an increase in the photoinitiator concentration in the dispersed phase by 2 times up to 4 wt%. Without such an increase in concentration, the minimal PEGDA MPs diameter was 80 µm.
According to the obtained results, the method proved to be quite universal and compatible with different configurations and sizes of microchannels, convenient to be used with UV-based and chemical hydrogel crosslinking methods through photo- and interfacial polymerization. The main limitation of the method is the need for uniform distribution and sufficient concentration of droplets in the electrocoalescence area for efficient and reproducible droplet merging. Additionally, formation of clusters from partly crosslinked MPs, united by electrocoalescence, may clog the channels of the microfluidic device making its further usage without careful washing quite difficult. Another limitation of the method is caused by the long time required for full crosslinking of hydrogels, which might be much longer than the traveling time of the droplets in a microfluidic device. To overcome it, the droplets can be incubated in a sample tube and then injected into a microfluidic channel or put on a microscopy slide for testing by electrocoalescence. Furthermore, ζ-potential of hydrogel microparticles may influence the merging dynamics of hydrogel droplets. The presence of surface charges creates repulsive Coulomb forces between like-charged droplets.85 Therefore, merging dynamics is determined by the balance between dielectrophoretic attraction and Coulomb repulsion, indicating that larger electric fields might be required for electrocoalescence of charged droplets.
Despite all the limitations, we believe that droplet electrocoalescence is an easy-to-use way for visual assessment or accurate characterization of W/O emulsions and hydrogel MPs. Further, by enabling in situ monitoring of gelation, our method provides a powerful tool for developing and improving highly efficient, stable and reproducible synthesis of MPs with a complex hierarchy and compartmentalization structure for advanced capsules and drug carriers, which still remains challenging in the field of material science.
Conflicts of interest
NF and AB are cofounders of JSC “Flixbio” exploiting and commercializing microfluidic technologies. AT, NF and AB filled in a patent application form.Data availability
All data and code required to reproduce the results in this article, including raw microscope image sequence files and Python scripts for video processing and analysis using OpenCV, are available from the Zenodo repository, DOI: https://doi.org/10.5281/zenodo.14970355. The Python scripts uploaded to the GitHub repository at https://github.com/Andrey12133/droplets-tracking.git.Supplementary information provides additional experimental details, characterization and statistical data, and COMSOL Multiphysics simulation results supporting the article. See DOI: https://doi.org/10.1039/d5sm01068c.
Acknowledgements
The study was supported by the Russian Science Foundation, project 20-74-10117, https://rscf.ru/project/20-74-10117/.Notes and references
- W. Li, L. Zhang, X. Ge, B. Xu, W. Zhang, L. Qu, C.-H. Choi, J. Xu, A. Zhang and H. Lee, et al. , Chem. Soc. Rev., 2018, 47, 5646–5683 RSC.
- A. Choi, K. D. Seo, B. C. Kim and D. S. Kim, et al. , Lab Chip, 2017, 17, 591–613 RSC.
- C. Tan and D. J. McClements, Foods, 2021, 10, 812 CrossRef CAS.
- J. Kozlowska, W. Prus and N. Stachowiak, Int. J. Biol. Macromol., 2019, 129, 952–956 CrossRef CAS PubMed.
- Y.-X. Ren, X. Zeng, L.-M. Zhou, C. Kong, H. Mao, C.-W. Qiu, K. K. Tsia and K. K. Wong, ACS Photonics, 2020, 7, 1483–1490 CrossRef CAS.
- H. Wang, S. C. Leeuwenburgh, Y. Li and J. A. Jansen, Tissue Eng., Part B, 2012, 18, 24–39 CrossRef CAS PubMed.
- M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146–2155 RSC.
- L. Chen, A. Chen, X. D. Zhang, M. T. Saenz Robles, H.-S. Han, Y. Xiao, G. Xiao, J. M. Pipas and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2404727121 CrossRef CAS.
- G. Turnbull, J. Clarke, F. Picard, P. Riches, L. Jia, F. Han, B. Li and W. Shu, Bioact. Mater., 2018, 3, 278–314 Search PubMed.
- X. Mao, M. Wang, S. Jin, J. Rao, R. Deng and J. Zhu, J. Polym. Sci., 2022, 60, 1653–1669 CrossRef CAS.
- Y. Cao, J. Tan, H. Zhao, T. Deng, Y. Hu, J. Zeng, J. Li, Y. Cheng, J. Tang and Z. Hu, et al. , Nat. Commun., 2022, 13, 7463 CrossRef CAS.
- S. Bhatia, U. Balis, M. Yarmush and M. Toner, FASEB J., 1999, 13, 1883–1900 CrossRef CAS.
- K. Saralidze, L. H. Koole and M. L. Knetsch, Materials, 2010, 3, 3537–3564 CrossRef CAS.
- J. Yeh, Y. Ling, J. M. Karp, J. Gantz, A. Chandawarkar, G. Eng, J. Blumling Iii, R. Langer and A. Khademhosseini, Biomaterials, 2006, 27, 5391–5398 CrossRef CAS PubMed.
- K. Seo, D. Kim and S. Sanchez, Lab Chip, 2015, 15, 3622–3626 RSC.
- D. Dendukuri and P. S. Doyle, Adv. Mater., 2009, 21, 4071–4086 CrossRef CAS.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- J. H. Kim, T. Y. Jeon, T. M. Choi, T. S. Shim, S.-H. Kim and S.-M. Yang, Langmuir, 2014, 30, 1473–1488 CrossRef CAS.
- J. Wang, Y. Li, X. Wang, J. Wang, H. Tian, P. Zhao, Y. Tian, Y. Gu, L. Wang and C. Wang, Micromachines, 2017, 8, 22 CrossRef.
- T. Y. Lee, T. M. Choi, T. S. Shim, R. A. Frijns and S.-H. Kim, Lab Chip, 2016, 16, 3415–3440 RSC.
- K. Belousov, N. Filatov, I. Kukhtevich, V. Kantsler, A. Evstrapov and A. Bukatin, Sci. Rep., 2021, 11, 8797 CrossRef CAS PubMed.
- P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446 RSC.
- E. Stolovicki, R. Ziblat and D. A. Weitz, Lab Chip, 2018, 18, 132–138 RSC.
- Q. Wu, X. Huang, R. Liu, X. Yang, G. Xiao, N. Jiang, D. A. Weitz and Y. Song, Langmuir, 2023, 40, 1950–1960 CrossRef.
- D. J. McClements, Soft Matter, 2012, 8, 1719–1729 RSC.
- J. Bibette, F. L. Calderon and P. Poulin, Rep. Prog. Phys., 1999, 62, 969 CrossRef CAS.
- P. Gruner, B. Riechers, B. Semin, J. Lim, A. Johnston, K. Short and J.-C. Baret, Nat. Commun., 2016, 7, 10392 CrossRef CAS.
- K. Piradashvili, E. M. Alexandrino, F. R. Wurm and K. Landfester, Chem. Rev., 2016, 116, 2141–2169 CrossRef CAS.
- F. Scheffold, Nat. Commun., 2020, 11, 4315 CrossRef CAS PubMed.
- P. Patel and P. Thareja, Eur. Polym. J., 2022, 163, 110935 CrossRef CAS.
- V. S. Raghuwanshi and G. Garnier, Adv. Colloid Interface Sci., 2019, 274, 102044 CrossRef CAS.
- J. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 1–17 Search PubMed.
- Z. Dai and T. Ngai, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 2995–3003 CrossRef CAS.
- S. Abedi, N. S. Suteria, C.-C. Chen and S. A. Vanapalli, J. Colloid Interface Sci., 2019, 533, 59–70 CrossRef CAS.
- F. Del Giudice, G. D'Avino and P. L. Maffettone, Lab Chip, 2021, 21, 2069–2094 RSC.
- T. Heida, J. W. Neubauer, M. Seuss, N. Hauck, J. Thiele and A. Fery, Macromol. Chem. Phys., 2017, 218, 1600418 CrossRef.
- C. Duprat, H. Berthet, J. S. Wexler, O. Du Roure and A. Lindner, Lab Chip, 2015, 15, 244–252 RSC.
- A. Mietke, O. Otto, S. Girardo, P. Rosendahl, A. Taubenberger, S. Golfier, E. Ulbricht, S. Aland, J. Guck and E. Fischer-Friedrich, Biophys. J., 2015, 109, 2023–2036 CrossRef CAS PubMed.
- J. Lin, Q. Tang, D. Hu, X. Sun, Q. Li and J. Wu, Colloids Surf., A, 2009, 346, 177–183 CrossRef CAS.
- P. Kasak, J. Sasová, R. Shoheeduzzaman, M. T. Baig, A. A. H. Alyafei and J. Tkac, Emergent Mater., 2021, 4, 769–779 CrossRef CAS.
- R. Zvitov and A. Nussinovitch, Food Hydrocolloids, 2001, 15, 33–42 CrossRef CAS.
- J. S. Eow, M. Ghadiri, A. O. Sharif and T. J. Williams, Chem. Eng. J., 2001, 84, 173–192 CrossRef CAS.
- A. R. Abate, T. Hung, P. Mary, J. J. Agresti and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19163–19166 CrossRef CAS.
- B. Hu, S. Ye, D. Chen, B. Xie, R. Hu, Y. Qiao, Y. Yu, H. Yu, X. Zheng and Y. Lan, et al. , Anal. Chem., 2021, 93, 13112–13117 CrossRef CAS.
- N. Hauck, T. A. Neuendorf, M. J. Männel, L. Vogel, P. Liu, E. Stündel, Y. Zhang and J. Thiele, Soft Matter, 2021, 17, 10312–10321 RSC.
- A. Fallah-Araghi, J.-C. Baret, M. Ryckelynck and A. D. Griffiths, Lab Chip, 2012, 12, 882–891 RSC.
- C. Frey, K. Göpfrich, S. Pashapour, I. Platzman and J. P. Spatz, ACS Omega, 2020, 5, 7529–7536 CrossRef CAS PubMed.
- L. Mazutis, J. Gilbert, W. L. Ung, D. A. Weitz, A. D. Griffiths and J. A. Heyman, Nat. Protoc., 2013, 8, 870–891 CrossRef CAS.
- J. Panwar, A. Autour and C. A. Merten, Nat. Protoc., 2023, 18, 1090–1136 CrossRef CAS PubMed.
- R. Gaikwad and A. Sen, Analyst, 2021, 146, 95–108 RSC.
- J. Eggers, J. E. Sprittles and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2024, 57, 61–87 CrossRef.
- T. Leary, M. Yeganeh and C. Maldarelli, ACS Omega, 2020, 5, 7348–7360 CrossRef CAS.
- S. Chen, E. Pirhadi and X. Yong, J. Colloid Interface Sci., 2022, 618, 283–289 CrossRef CAS PubMed.
- P. J. Dekker, M. A. Hack, W. Tewes, C. Datt, A. Bouillant and J. H. Snoeijer, Phys. Rev. Lett., 2022, 128, 028004 CrossRef CAS PubMed.
- I. A. Latif, H. M. Abdullah and M. H. Saleem, Am. J. Polym. Sci., 2016, 6, 50–57 CAS.
- M. Füllbrandt, R. von Klitzing and A. Schönhals, Soft Matter, 2013, 9, 4464–4471 RSC.
- T. Yamamoto, T. Kurokawa, J. Ahmed, G. Kamita, S. Yashima, Y. Furukawa, Y. Ota, H. Furukawa and J. P. Gong, Soft Matter, 2014, 10, 5589–5596 RSC.
- Y. A. Meier, K. Zhang, N. D. Spencer and R. Simic, Langmuir, 2019, 35, 15805–15812 CrossRef CAS.
- V. Chokkalingam, Y. Ma, J. Thiele, W. Schalk, J. Tel and W. T. Huck, Lab Chip, 2014, 14, 2398–2402 RSC.
- A. Srivastava, S. Karthick, K. Jayaprakash and A. Sen, Langmuir, 2018, 34, 1520–1527 CrossRef CAS PubMed.
- M. Chabert, K. D. Dorfman and J.-L. Viovy, Electrophoresis, 2005, 26, 3706–3715 CrossRef CAS PubMed.
- A. S. Bukatin, I. S. Mukhin, E. Malyshev, I. Kukhtevich, A. A. Evstrapov and M. V. Dubina, Tech. Phys., 2016, 61, 1566–1571 CrossRef CAS.
- D. Qin, Y. Xia and G. M. Whitesides, Nat. Protoc., 2010, 5, 491 CrossRef CAS PubMed.
- S. Utech, R. Prodanovic, A. S. Mao, R. Ostafe, D. J. Mooney and D. A. Weitz, Adv. Healthcare Mater., 2015, 4, 1628–1633 CrossRef CAS PubMed.
- N. A. Filatov, I. A. Denisov, A. A. Evstrapov and A. S. Bukatin, IEEE Trans. Instrum. Meas., 2022, 71, 1–10 Search PubMed.
- R. O. Duda and P. E. Hart, Commun. ACM, 1972, 15, 11–15 CrossRef.
- T. Beatus, R. H. Bar-Ziv and T. Tlusty, Phys. Rep., 2012, 516, 103–145 CrossRef.
- T. Beatus, I. Shani, R. H. Bar-Ziv and T. Tlusty, Chem. Soc. Rev., 2017, 46, 5620–5646 RSC.
- T. Beatus, T. Tlusty and R. Bar-Ziv, Nat. Phys., 2006, 2, 743–748 Search PubMed.
- A. H. Kumar, S. J. Thomson, T. R. Powers and D. M. Harris, Phys. Rev. Fluids, 2021, 6, 094501 Search PubMed.
- W. S. Cleveland, J. Am. Stat. Assoc., 1979, 74, 829–836 CrossRef.
- L. Mazutis, R. Vasiliauskas and D. A. Weitz, Macromol. Biosci., 2015, 15, 1641–1646 CrossRef CAS PubMed.
- H. Zhang, E. Tumarkin, R. Peerani, Z. Nie, R. M. A. Sullan, G. C. Walker and E. Kumacheva, J. Am. Chem. Soc., 2006, 128, 12205–12210 CrossRef CAS PubMed.
- B. Yang, Y. Lu and G. Luo, Ind. Eng. Chem. Res., 2012, 51, 9016–9022 CrossRef CAS.
- F. Di Lorenzo and S. Seiffert, Macromol. React. Eng., 2016, 10, 201–205 CrossRef CAS.
- K. Krutkramelis, B. Xia and J. Oakey, Lab Chip, 2016, 16, 1457–1465 RSC.
- D. Debroy, J. Oakey and D. Li, J. Colloid Interface Sci., 2018, 510, 334–344 CrossRef CAS PubMed.
- M. M. Villone and P. L. Maffettone, Rheol. Acta, 2019, 58, 109–130 CrossRef CAS.
- D. Heyes and A. Brańka, Soft Matter, 2009, 5, 2681–2685 RSC.
- L. Rovigatti, N. Gnan, A. Ninarello and E. Zaccarelli, Macromolecules, 2019, 52, 4895–4906 CrossRef CAS.
- G. M. Kavanagh and S. B. Ross-Murphy, Prog. Polym. Sci., 1998, 23, 533–562 CrossRef CAS.
- I. F. Farrés and I. Norton, Food Hydrocolloids, 2014, 40, 76–84 CrossRef.
- D. Calvet, J. Y. Wong and S. Giasson, Macromolecules, 2004, 37, 7762–7771 CrossRef CAS.
- J. Mandal, K. Zhang and N. D. Spencer, et al. , Soft Matter, 2021, 17, 6394–6403 RSC.
- X. Luo, H. Yin, J. Ren, H. Yan, Y. Lü and L. He, J. Phys. Chem. C, 2019, 123, 19588–19595 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |









