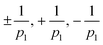Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A spectrum of p-atic symmetries and defects in confluent epithelia
Lea
Happel
 a,
Griseldis
Oberschelp
a,
Griseldis
Oberschelp
 a,
Anneli
Richter
a,
Anneli
Richter
 a,
Gwenda Roselene
Rode
a,
Gwenda Roselene
Rode
 a,
Valeriia
Grudtsyna
a,
Valeriia
Grudtsyna
 b,
Amin
Doostmohammadi
b,
Amin
Doostmohammadi
 b and
Axel
Voigt
b and
Axel
Voigt
 *acd
*acd
aInstitute of Scientific Computing, TU Dresden, 01062 Dresden, Germany. E-mail: axel.voigt@tu-dresden.de
bNiels Bohr Institute, University of Copenhagen, Kobenhavn, 2100, Denmark
cCenter for Systems Biology (CSBD), Pfotenhauerstr. 108, 01307 Dresden, Germany
dCluster of Excellence, Physics of Life, TU Dresden, Arnoldstr. 18, 01307 Dresden, Germany
First published on 6th January 2026
Abstract
Topological defects provide a unifying language to describe how orientational order breaks down in active and living matter. Considering cells as elongated particles confluent, epithelial tissues can be interpreted as nematic fields and their defects have been linked to extrusion, migration, and morphogenetic transformations. Yet, epithelial cells are not restricted to nematic order: their irregular shapes can express higher rotational symmetries, giving rise to p-atic order with p > 2. Here we introduce a framework to extract p-atic fields and their defects directly from experimental images. Applying this method to MDCK cells, we find that all symmetries from p = 2 to p = 6 generate  defects. Surprisingly, the statistics reveal an even–odd asymmetry, with odd p producing more defects than even p, consistent with geometric frustration arguments based on tilings. In contrast, no strong positional or orientational correlations are found between nematic and hexatic defects, suggesting that different symmetries coexist largely independently. These results demonstrate that epithelial tissues should not be described by nematic order alone, but instead host a spectrum of p-atic symmetries. Our work provides experimental evidence for this multivalency of order and offers a route to test and refine emerging p-atic liquid crystal theories of living matter.
defects. Surprisingly, the statistics reveal an even–odd asymmetry, with odd p producing more defects than even p, consistent with geometric frustration arguments based on tilings. In contrast, no strong positional or orientational correlations are found between nematic and hexatic defects, suggesting that different symmetries coexist largely independently. These results demonstrate that epithelial tissues should not be described by nematic order alone, but instead host a spectrum of p-atic symmetries. Our work provides experimental evidence for this multivalency of order and offers a route to test and refine emerging p-atic liquid crystal theories of living matter.
Introduction
Topological defects—localized disruptions of orientational order—are emerging as universal signatures of organization in living matter. In confluent epithelia, where cell shapes define coarse-grained orientational fields, the creation, motion, and annihilation of defects are closely tied to morphogenetic processes. There is increasing evidence that the shape of cells and resulting orientational order and associated topological defects are essential for mechanical mechanisms that drive morphogenetic processes during embryonic development. Considering for example the elongation of cells to define a coarse-grained nematic order1–3 allows to describe properties of the tissue. Corresponding topological defects have been related to cell extrusions,2,4 morphological changes5 and active turbulence.6 The underlying coarse-grained theories are nematic liquid crystal theories based on Oseen–Frank and Landau–de Gennes energies,7 which if combined with flow lead to Ericksen–Leslie and Beris–Edwards models, respectively. These theories have successfully captured a wide range of epithelial phenomena and established defects as key organizing elements of tissue mechanics.Beyond the nematic case (p = 2), higher order rotational symmetries have recently been reported in both biological and synthetic systems, e.g. ref. 8 for tetratic order (p = 4) and ref. 9–13 for hexatic (p = 6) order. In contrast with nematic order, which represents rotational symmetries under rotation by π, tetratic and hexatic order considers rotational symmetry under rotation by 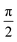 and
and 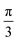 , respectively. This classification can be extended to define p-atic order, which considers rotational symmetry under rotation by
, respectively. This classification can be extended to define p-atic order, which considers rotational symmetry under rotation by 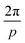 , with p an integer. Liquid crystal phases with p-atic order have a long history, starting with Onsager who showed that the symmetry and shape of constituent particles can lead to p-atic order.14 Most prominently, hexatic order has been postulated and found by experiments and simulations as an intermediate state between crystalline solid and isotropic liquid in.15–21 Other examples are colloidal systems for triadic platelets22 or cubes,23 which lead to p-atic order with p = 3 and p = 4, respectively. Even pentatic (p = 5) and heptatic (p = 7) liquid crystals have been engineered by combining different colloidal tiles.24,25 First models for such systems go back to26 and can be viewed as extensions of Oseen–Frank-like models, accounting for higher rotational symmetries of the director field. More recently liquid crystal theories for p-atic order which extend the Landau–de Gennes approach have been proposed.27,28 These models consider higher order Q-tensors and couple them with fluid flow. Active extensions of these theories predict defect creation, currents, and instabilities whose quantization depends on p, pointing to qualitatively new physics in living matter. These theories have already been used to model epithelial tissue.12,29,30 What remains open, however, is how the irregular and dynamic shapes of epithelial cells give rise to p-atic fields and defects, and how these connect to the continuum predictions. Our work addresses this gap by showing that epithelial cell shapes naturally encode multiple p-atic orders and by directly quantifying their defect content.
, with p an integer. Liquid crystal phases with p-atic order have a long history, starting with Onsager who showed that the symmetry and shape of constituent particles can lead to p-atic order.14 Most prominently, hexatic order has been postulated and found by experiments and simulations as an intermediate state between crystalline solid and isotropic liquid in.15–21 Other examples are colloidal systems for triadic platelets22 or cubes,23 which lead to p-atic order with p = 3 and p = 4, respectively. Even pentatic (p = 5) and heptatic (p = 7) liquid crystals have been engineered by combining different colloidal tiles.24,25 First models for such systems go back to26 and can be viewed as extensions of Oseen–Frank-like models, accounting for higher rotational symmetries of the director field. More recently liquid crystal theories for p-atic order which extend the Landau–de Gennes approach have been proposed.27,28 These models consider higher order Q-tensors and couple them with fluid flow. Active extensions of these theories predict defect creation, currents, and instabilities whose quantization depends on p, pointing to qualitatively new physics in living matter. These theories have already been used to model epithelial tissue.12,29,30 What remains open, however, is how the irregular and dynamic shapes of epithelial cells give rise to p-atic fields and defects, and how these connect to the continuum predictions. Our work addresses this gap by showing that epithelial cell shapes naturally encode multiple p-atic orders and by directly quantifying their defect content.
Rather than proposing a new methodology per se, we use Minkowski tensor–based shape descriptors as a lens to reveal previously hidden physics: the coexistence of distinct p-atic orders and their defect networks in confluent epithelial tissues. Our approach starts from quantified rotational symmetries of rounded and irregular cell shapes, see Fig. 1. These data show a snapshot of the raw experimental data of a MDCK (Madin–Darby Canine Kidney) cell monolayer, together with segmented cell shapes and their shape classification by Minkowski tensors for various p, visualized by the orientation ϑp, see ref. 31 for details. The considered Minkowski tensors use contour integrals of the cell boundaries and have been shown to be robust and advantageous to other shape characterization methods, such as the bond order parameter4,32 or the shape function.12 Using these per-cell measurements as inputs, we construct continuous p-atic fields at user-controlled coarse-graining radii. We provide visualization tools that help to identify the essential information of p-atic liquid crystals. Here we draw connections to computer graphics, where director fields with higher rotational symmetries are known as rotational symmetry (RoSy) fields33,34 and also the connection between higher order Q-tensor fields and these RoSy-fields has been established and used for visualization.34 We essentially follow35 and use the line integral convolution (LIC) technique for each direction and blend the results. This provides a high contrast texture-based image of the coarse-grained orientation ϑp. The second aspect concerns the identification of topological defects. While various approaches for this task have been proposed36,37 we here follow our experience in nematic fields and consider the intersection points of zero contour lines to identify defects. This provides the points at which the Q-tensor is singular. As also for higher order Q-tensors the irreducible information is contained in only two linearly independent components, their zero-contours are sufficient to determine the defects. After the locations are identified the topological charge follows by computing the winding number.
We only found defects of topological charge 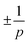 . While other defects are theoretically possible the ones found are energetically most favorable. Placing these defects atop the LIC textures provides an intuitive, symmetry-aware overview that scales cleanly from p = 2 to higher p. Statistics on these defects reveal an even-odd asymmetry but do not show strong correlations between defects of different p-atic order. Together, these analyses uncover that epithelial tissues harbor a spectrum of topological defects across multiple symmetries—an observation that calls for new coarse-grained descriptions beyond the nematic paradigm.
. While other defects are theoretically possible the ones found are energetically most favorable. Placing these defects atop the LIC textures provides an intuitive, symmetry-aware overview that scales cleanly from p = 2 to higher p. Statistics on these defects reveal an even-odd asymmetry but do not show strong correlations between defects of different p-atic order. Together, these analyses uncover that epithelial tissues harbor a spectrum of topological defects across multiple symmetries—an observation that calls for new coarse-grained descriptions beyond the nematic paradigm.
The provided tools are not only applicable for experimental data of confluent monolayers of MDCK cells, the tools can also be applied to computational results of cell-resolved models,38 as well as coarse-grained models for p-atic liquid crystals27,28 and therefore allow for a direct comparison. By establishing this bridge, we enable direct confrontation between cell-resolved data and continuum p-atic theories, and reveal new physics in how multiple orientational symmetries coexist and organize in living tissues. For all tasks we provide the considered Python code, see ref. 39.
Materials and methods
All steps from cell shapes to tissue-scale p-atic defects are illustrated in Fig. 2. Therefore again the snippet from Fig. 1(b) is used. We briefly motivate each step physically before giving the implementation. | ||
| Fig. 2 Illustration of how we go from the orientation of cells (left column) to a fine orientation field (middle columns), which we then visualize as a LIC image (the two right most columns) and use to detect defects (right column). In this illustration a coarse-graining radius ravg of 1.5rmax(t) is used. Positively charged defects are indicated by an open circle and negatively charged defects by a closed circle. Different colors are used for different p, corresponding to the color scheme used in Fig. 1. The pictures on the left correspond to the pictures on Fig. 1. | ||
Computing (irreducible) Minkowski tensors for each cell
The first step for constructing a global p-atic field is to calculate ϑp and qp for every cell. As the general framework used for this – (irreducible) Minkowski tensors or equivalently higher order Q-tensors – is already described in detail in numerous publications, we will only motivate the method and focus on the specific data format. Physically, these descriptors quantify how closely a cell shape expresses a p-fold rotational symmetry (e.g., rod-like for p = 2, square-like for p = 4, hexagon-like for p = 6), and thus generalize nematic order to arbitrary p.From the microscopy image, which can be seen for example in Fig. 1(a), a cell segmentation is generated. This segmentation is stored as grayscale image, whereby every cell is associated to a different value. Firstly we extract the contour ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) of each cell, using the contour function from scikit-image.40 To remove pixel-shaped artifacts, we slightly smooth out this contour
of each cell, using the contour function from scikit-image.40 To remove pixel-shaped artifacts, we slightly smooth out this contour ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) . This smoothing avoids spurious high-frequency contributions to ψp from jagged pixel edges and yields robust shape integrals. We can then use the outward pointing normal n of this contour to calculate
. This smoothing avoids spurious high-frequency contributions to ψp from jagged pixel edges and yields robust shape integrals. We can then use the outward pointing normal n of this contour to calculate
 | (1) |
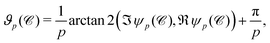 | (2) |
 | (3) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) corresponding to the length of the contour multiplied with the factor
) corresponding to the length of the contour multiplied with the factor  , measures how strongly the shape exhibits p-fold symmetry. The division by ψ0(
, measures how strongly the shape exhibits p-fold symmetry. The division by ψ0(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) is needed to ensure scale invariance. In other words, qp is a dimensionless “strength” of p-aticity independent of cell size.
) is needed to ensure scale invariance. In other words, qp is a dimensionless “strength” of p-aticity independent of cell size.
In this paper we are mainly concerned with the orientation ϑp. An illustration of the orientation of different cells for p ∈ [2, 3, 4, 5, 6] is shown in Fig. 1 and 2. These per-cell orientations are the inputs to the tissue-level fields analyzed below.
Generation of coarse-grained p-atic fields
We now use the orientations ϑp of the individual cells to obtain a global orientation field via interpolation. As we understand the global orientation field and with this its defects as a tissue and not a cell property we also use some averaging in the process to smooth the global field. Of course the extent of this averaging will influence the obtained field and with it the number and the location of the defects. Roughly said more averaging leads to smoother fields and a smaller number of defects. To account for this we consider three different radii for averaging to investigate if the qualitative behavior is independent of the extent of averaging. We will also refer to this averaging as coarse-graining in the following. Physically, the coarse-graining radius ravg defines the observation scale: larger ravg probes longer wavelengths and emphasizes tissue-level organization over cell-scale variability.For the context of averaging, interpolating and finally detecting the defect location we will not use ϑp and qp but the related higher order Q-tensor representation. The reason for this is twofold: on the one hand, Q-tensors of order p naturally encode the invariance under rotations of  . On the other hand these Q-tensor fields are well suited for defect detection, as defects are singular points in this defect field, meaning points where all linear independent components of this Q-tensor are zero. This representation also avoids branch-cut ambiguities in angles and makes zero-set geometry well defined.
. On the other hand these Q-tensor fields are well suited for defect detection, as defects are singular points in this defect field, meaning points where all linear independent components of this Q-tensor are zero. This representation also avoids branch-cut ambiguities in angles and makes zero-set geometry well defined.
In 2D Q-tensors have effectively two independent components Q0 and Q1, for the reduced (irreducible) description we use, independent of order p. We therefore firstly calculate these two components from ϑp(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) as
) as
Q0(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) = cos(pϑp( ) = cos(pϑp(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) )), Q1( )), Q1(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) = sin(pϑp( ) = sin(pϑp(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) )). )). | (4) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) )i1i2…ip of Q(
)i1i2…ip of Q(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) with an even number of ones in the indexes are proportional to Q0(
) with an even number of ones in the indexes are proportional to Q0(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) and all elements with an odd number of ones in the indexes are proportional to Q1(
) and all elements with an odd number of ones in the indexes are proportional to Q1(![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ).12 Note that in the implementation summation formulas for this are used. Expressing the field as (Q0, Q1) means that all physically equivalent orientations related by 2π/p map to the same point on the unit circle in this space.
).12 Note that in the implementation summation formulas for this are used. Expressing the field as (Q0, Q1) means that all physically equivalent orientations related by 2π/p map to the same point on the unit circle in this space.
We then calculated an averaged and interpolated orientation for each point on the fine regular grid to obtain a global field. We denote the j-th cell as ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) j and its midpoint as cj. Then the formula for the value of a grid point xifine on the fine grid reads as follows:
j and its midpoint as cj. Then the formula for the value of a grid point xifine on the fine grid reads as follows:
 | (5) |
 | (6) |
 as
as | (7) |
| g(d) = max(ravg − d, 0.0) | (8) |
Localization of defects
Defects are singularities in the Q-tensor field, which means the Q-tensor is the 0-tensor at defects. As there are only two independent components this corresponds to Qint0(xifine) = 0.0 and Qint1(xifine) = 0.0. Geometrically, these are intersection points of the two zero-contours, i.e., locations where the local orientation is undefined. Exploiting this, we detect defect locations as the intersections of the contour lines of| Qint0(xfine) = 0.0 and Qint1(xfine) = 0.0. |
Other methods, precisely the usage of the Dirichlet energy or the Jacobian determinant, were tested, but in our data lead to a higher number of false-positive results. We therefore adopted the zero-level–set intersection criterion for its robustness and interpretability.
Calculation of the winding number
To detect the type of defect we closely follow the definition of the winding number | (9) |
Implementation-wise, we extract a closed path around the defect. To be precise we use a square-path for this, where the sides of the square have a distance of 4 pixels to the defect location. We then extract the corresponding eigenvectors along this path and align their orientation. Aligning the orientation means that we start at an arbitrary point on the path with an arbitrary orientation. Arbitrary here refers to the fact that we have p equivalent directions to choose from, which correspond to the p legs of the p-atic star. The resulting winding number is independent of the choice of the starting orientation, therefore this is arbitrary. We then consider two neighboring orientations, step by step in counter-clockwise direction. Aligning now means that we always consider the two orientations which enclose an angle  . Note that it is crucial to close the path by aligning the last eigenvector of the path with a copy of the eigenvector with which we started. Summing up all the angles between two neighboring vectors and dividing this sum by 2π gives the winding number. This method also ensures that the resulting winding number is a multiple of
. Note that it is crucial to close the path by aligning the last eigenvector of the path with a copy of the eigenvector with which we started. Summing up all the angles between two neighboring vectors and dividing this sum by 2π gives the winding number. This method also ensures that the resulting winding number is a multiple of  . This alignment procedure removes artificial jumps and ensures that the measured ω captures the intrinsic rotation of the field.
. This alignment procedure removes artificial jumps and ensures that the measured ω captures the intrinsic rotation of the field.
Note that this method assumes that there are no jumps of  or larger between two neighboring vectors. In practice, this assumption is satisfied away from regions of very low qp, where orientations are poorly defined.
or larger between two neighboring vectors. In practice, this assumption is satisfied away from regions of very low qp, where orientations are poorly defined.
Calculation of the direction of  defects
defects
Defects with a winding number of  are comet-shaped, as can be seen for example in Fig. 3, and with this have a directionality. This polarity is unique among defects in our dataset and enables spatio-orientational comparisons across symmetries. To calculate this we follow.41,42 We calculate a tensor
are comet-shaped, as can be seen for example in Fig. 3, and with this have a directionality. This polarity is unique among defects in our dataset and enables spatio-orientational comparisons across symmetries. To calculate this we follow.41,42 We calculate a tensorwhereby ϑi2 denotes the orientation for p = 2 at the grid-point i of the fine regular grid. Then we get the orientation
 of the defect as
of the defect asHereby 〈·,·〉 denotes the average along a short loop around the
 defect in question. For this loop we again choose a square-path, where the sides of the square have a distance of 4 pixels to the defect location. We use this direction in Section Results to test for alignment with hexatic defects.
defect in question. For this loop we again choose a square-path, where the sides of the square have a distance of 4 pixels to the defect location. We use this direction in Section Results to test for alignment with hexatic defects.
 | ||
Fig. 3
 and and  defects shown as described in ref. 35. For the LIC filter the vtkSurfaceLICMapper from vtk43 was used, which is implemented based on the ideas from ref. 44. Positively charged defects are indicated by an open circle and negatively charged defects by a closed circle. Different colors are used for different p, corresponding to the color scheme used in Fig. 1. defects shown as described in ref. 35. For the LIC filter the vtkSurfaceLICMapper from vtk43 was used, which is implemented based on the ideas from ref. 44. Positively charged defects are indicated by an open circle and negatively charged defects by a closed circle. Different colors are used for different p, corresponding to the color scheme used in Fig. 1. | ||
Visualization
To visualize the p-atic fields we follow35 and use the line integral convolution (LIC) technique for each direction and blend the resulting images. This provides a high contrast texture-based image of the coarse-grained orientation ϑp. For higher p, the blending across equivalent directions yields symmetry-aware textures in which the p-leg structure is visually apparent. Topological defects already become visible as singular points in these fields. To further guide the eye we plot the identified defects together with their charge on top. Fig. 3 provides a classification of the considered defects with p = 2, 3, 4, 5, 6.
defects with p = 2, 3, 4, 5, 6.
Experimental setup
Results
We are mainly interested in qualitative correlations between defects of different orders. Before turning to such correlations, we first establish the basic statistics of defect formation across scales of observation. As there is no clear indication about the best coarse-graining radius ravg we systematically explore three different radii, ravg = 1.5rmax(t), ravg = 2.25rmax(t) and ravg = 3.0rmax(t). We use the full frames of the experimental data to calculate a global orientation field and the p-atic defects thereof. For all three different radii only defects were detected. This observation is fully consistent with continuum theory, where
defects were detected. This observation is fully consistent with continuum theory, where  charges are the lowest-energy topological excitations in p-atic fields.
charges are the lowest-energy topological excitations in p-atic fields.
As can be already seen in Fig. 4 a bigger coarse graining radius leads to a smaller number of defects. This scale dependence reflects the fact that coarse-graining suppresses short-wavelength fluctuations, smoothing out smaller defect–antidefect pairs. One can also already suspect from this, especially comparing frame 0 and frame 50, that the number of defects grows over time. This temporal increase suggests that as the monolayer becomes denser and more crowded, cell-shape irregularities continuously seed new orientational defects.
 | ||
| Fig. 4 Defect position for different coarse-graining radii ravg at different times. Different colors are used for different p, corresponding to the color scheme used in Fig. 1. Positively charged defects are indicated by an open circle and negatively charged defects by a closed circle. The raw experimental image for Frame 0 can be seen in Fig. 1(a), the one for Frame 25 in Fig. 11 and the one for Frame 50 in Fig. 12. | ||
To quantify these observations we evaluate the number of  defects over time. For this and all following evaluations we exclude all defects with a distance smaller than ravg to any domain boundary to ensure that our evaluations do not include boundary effects. As can be seen in Fig. 5 for all defect types and all ravg the number of defects grows over time. This is likely connected to the growing number of cells and the growing cell density over time. As expected from topological charge conservation, the numbers of
defects over time. For this and all following evaluations we exclude all defects with a distance smaller than ravg to any domain boundary to ensure that our evaluations do not include boundary effects. As can be seen in Fig. 5 for all defect types and all ravg the number of defects grows over time. This is likely connected to the growing number of cells and the growing cell density over time. As expected from topological charge conservation, the numbers of  and
and  defects are very close to each other and are barely distinguishable in Fig. 5. Especially for ravg = 1.5rmax(t) the numbers of defects corresponding to an odd p, so to p = 3 or p = 5, are noticeable higher than the numbers of defects for even p. This even–odd asymmetry becomes less prominent as ravg increases, suggesting that it originates from local tiling constraints of individual cell shapes rather than global tissue organization.
defects are very close to each other and are barely distinguishable in Fig. 5. Especially for ravg = 1.5rmax(t) the numbers of defects corresponding to an odd p, so to p = 3 or p = 5, are noticeable higher than the numbers of defects for even p. This even–odd asymmetry becomes less prominent as ravg increases, suggesting that it originates from local tiling constraints of individual cell shapes rather than global tissue organization.
 | ||
Fig. 5 Number of  and and  defects over time for different coarse-graining radii ravg. Different colors are used for different p, corresponding to the color scheme used in Fig. 1. The curves for defects over time for different coarse-graining radii ravg. Different colors are used for different p, corresponding to the color scheme used in Fig. 1. The curves for  and and  defects are almost on top of each other. defects are almost on top of each other. | ||
While it is hardly possible to pin down an exact reason for this, an intuitive explanation can be found by thinking about tilings made out of the corresponding reference shapes for different p. For p = 4 and p = 6 one can easily imagine a tiling of the space with only squares or only regular hexagons, see Fig. 6(b) and (c) for an illustration. Importantly, the orientation ϑ4 of the squares or ϑ6 of the hexagons is the same for all tiles. So it is possible to construct an ordered phase without any defects out of these reference shapes for p = 4 and p = 6.
 | ||
| Fig. 6 Tilings of the reference shapes for p = 3 (a) with (equilateral triangles), p = 4 (b) (with squares) and p = 6 (c) (with hexagons). | ||
For p = 3 and p = 5 the situation is different. The reference shape corresponding to p = 3 is an equilateral triangle. While it is possible to tile the space with this shape, neighboring triangles need to be rotated by 60°, see the illustration in Fig. 6(a). Therefore the associated orientations ϑ3 of neighboring triangles are orthogonal (with respect to p = 3) to each other, and this tiling of the space is not ordered and therefore would also not be defect free. For p = 5 the situation is even worse, as it is not possible to tile the space with regular pentagons. p = 2 is not regarded, as the associated shape for this is a line and therefore degenerate. However, it is possible to construct an ordered tiling of the space with rectangles elongated along one axis, leading to a defect-free nematic state described by ϑ2. In these cases of tilings with the reference shapes it is natural to expect that the number of defects for odd p will be higher than the number of defects for even p. Even though real epithelial tissues are far from perfect tilings and consist of highly irregular cell shapes, this geometric frustration argument provides a simple physical rationale for the observed odd–even asymmetry in defect statistics.
A more central question in the current literature is whether orientational orders of different symmetry coexist in a correlated way, and whether their associated defects are spatially coupled. For this we first investigate the distance between a defect of order p1 to the closest defect of order p2, similar to the evaluations in ref. 49. For p1 and p2 we consider all possible combinations of  defects, only
defects, only  defects, and only
defects, and only 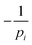 defects, i ∈ {1, 2}.
defects, i ∈ {1, 2}.
We then compare the distribution of distances from a specific kind of defect of order p1 to a specific kind of defect of order p2 to the distribution of distances from any grid point to the same kind of defects of order p2, using the Kolmogorov–Smirnov (KS) test. This test measures the maximum distance between the cumulative distribution functions of the two distributions. By construction, values close to 0 indicate that the two distributions are nearly identical, whereas values close to 1 reflect strong differences. If defects of order p1 and p2 were tightly coupled, we would expect large KS values.
We report the obtained KS values for all combinations Fig. 13 for ravg = 1.5rmax(t), Fig. 14 for ravg = 2.25rmax(t), and Fig. 15 for ravg = 3.0rmax(t). To allow readers to easily distinguish between low and high values, the tables are color-coded, from green/blue for values <0.1 to purple/orange for values >0.1. Across all cases, the KS test yields values below 0.1, indicating that the distributions are similar and that there is no strong positional correlation between distinct defect types.
To assess the statistical robustness of these comparisons we also examined the p-values of the KS test (Fig. 16–18). In this context p measures the probability of obtaining the observed results. A low p-value (≤0.05) indicates that the difference between distributions is significant, while higher values indicate that no statistically significant difference can be established. As expected, p-values tend to decrease with decreasing coarse-graining radius, since more defects provide larger sample sizes. However, these small differences are not our main focus: we are interested in whether correlations are both statistically significant and physically meaningful.
To address this, we directly compared the density functions of the distances between nematic (p = 2) and hexatic (p = 6) defects, as this pair has been the subject of recent debate.12,49,50 As shown in Fig. 7 and 8, the distance distributions between nematic and hexatic defects are nearly indistinguishable from those obtained by random grid points. From this we conclude that, within our experimental resolution, there is no tight spatial correlation between p = 2 and p = 6 defects.
The distance-based analysis above probes positional correlations only, without considering relative orientations. To fully test whether different defect types interact in a directional manner, we next analyzed spatio–orientational correlations. We restrict this investigation to  defects because these are the only defects detected in our data that have a directionality. All other defects have some rotational symmetry, for example
defects because these are the only defects detected in our data that have a directionality. All other defects have some rotational symmetry, for example  defects have a symmetry under a rotation of 120° and are therefore not regarded here.
defects have a symmetry under a rotation of 120° and are therefore not regarded here.
We now evaluate the angle between the orientation of the  defect and the closest
defect and the closest  ,
,  , or
, or  defect, and show the resulting density functions as polar plots in Fig. 10. The measured angle is illustrated in Fig. 9. By construction, a peak at 0° would indicate that hexatic defects tend to localize at the tail of a
defect, and show the resulting density functions as polar plots in Fig. 10. The measured angle is illustrated in Fig. 9. By construction, a peak at 0° would indicate that hexatic defects tend to localize at the tail of a  defect, whereas a peak at 180° would indicate alignment with the head.
defect, whereas a peak at 180° would indicate alignment with the head.
 | ||
Fig. 9 Illustration of the measured angle in Fig. 10. The cell outlines for the corresponding part of the experimental image are shown in (a), the LIC images with the defects for p = 2 and p = 6 are shown in (b) and (c), respectively. For the  defect additionally the direction of the tail is marked. In (d) the defect positions for p = 2 and p = 6 are shown and the angle between the tail of the defect additionally the direction of the tail is marked. In (d) the defect positions for p = 2 and p = 6 are shown and the angle between the tail of the  defect and the closest defect and the closest  defect is marked with α. As the closest defect is marked with α. As the closest  defect is directly under the tail the angle between it and the tail of the defect is directly under the tail the angle between it and the tail of the  defect would be 0°. defect would be 0°. | ||
 | ||
Fig. 10 Density function of the angles between the orientation of a  defect and the closest defect and the closest  defect. An angle of 0° means that the closest defect. An angle of 0° means that the closest  defect lies at the tail of the defect lies at the tail of the  defect, an angle of 180° means that the closest defect, an angle of 180° means that the closest  defect lies at the head of the defect lies at the head of the  defect. The orientation of the defect. The orientation of the  is calculated according to ref. 41. The axis scaling is the same in all plots. is calculated according to ref. 41. The axis scaling is the same in all plots. | ||
Across all coarse-graining radii, evaluating these density functions for all found types of hexatic defects reveals that there is no spatio–orientational connection to the orientation of  defects. This lack of alignment further supports the conclusion that nematic and hexatic defects in epithelial monolayers emerge largely independently, without systematic coupling at the level of defect orientation.
defects. This lack of alignment further supports the conclusion that nematic and hexatic defects in epithelial monolayers emerge largely independently, without systematic coupling at the level of defect orientation.
Discussion
Independent of the coarse-graining radius ravg, no connection between the locations of defects of different p-atic order could be found, and in particular we did not detect correlations between nematic and hexatic defects. While there are some studies on experimental data that include investigations of defect numbers,12,13 studies focusing on defect positions are mainly restricted to computational data.49,50 A direct comparison of our results with49,50 is not possible for two reasons:1. In both studies orientational defects are used for nematic order, but positional defects are used for hexatic order. While positional and orientational defects can be tightly related in cellular tissues, especially in a state close to the solid phase, they are not the same and we aim to keep them clearly separated. Positional defects are inherently tied to the cell scale, whereas orientational defects can be probed across multiple length scales depending on the averaging radius. By restricting our analysis to orientational defects, we access tissue-level symmetries rather than cell-level packing irregularities.
2. The studies49,50 mainly focus on the solid phase of tissue, which does not correspond to our data, which are in the fluid phase. However, in ref. 50 it is reported that the correlation between hexatic and nematic defects weakens when going from the solid to the fluid phase. This trend is in agreement with what we see in our data. Our results therefore extend these observations into the regime where cells continuously divide, rearrange, and remodel their shapes.
More broadly, our analysis demonstrates that constructing global p-atic fields and detecting defects therein provides a powerful bridge between experimental data or agent-based models of cells and coarse-grained continuum descriptions. While first models including higher-order p-atics have been proposed27,28 and applied to epithelial tissues,12,29 it remains unclear which p-atic orders are most relevant. In this paper we treat all of them equally. As we did not find positional correlations between defects of distinct p, we propose that coarse-grained liquid crystal frameworks for epithelial tissue may need to integrate multiple p simultaneously. Following the same reasoning, the exclusive focus on the relation between p = 2 and p = 6 should be reconsidered. Indeed, our results (Fig. 5) suggest an intriguing even–odd effect in defect numbers, motivating further study. There is also no indication that p = 4 is less important: correlations between tetratic order and cell division have recently been reported,8 and it will be an interesting future direction to investigate whether tetratic defects are directly linked to cell division events.
Finally, the choice of length scale is crucial, both for constructing coarse-grained fields and for interpreting defect statistics. It remains unclear whether global fields and defects should be calculated closer to the cell scale or the tissue scale, and whether the same scale should be used for all defect types. Our findings suggest no clear dominance of one defect type at a given scale. However, mathematical tests in isolation cannot fully capture the underlying biological complexity. Connecting different defects to functional cellular or tissue-level processes—similar to how  defects were linked to cell extrusion2—could provide decisive insights. In this sense, the presence and dynamics of p-atic defects may serve not only as order-parameter singularities but also as markers of key biological events in morphogenesis.
defects were linked to cell extrusion2—could provide decisive insights. In this sense, the presence and dynamics of p-atic defects may serve not only as order-parameter singularities but also as markers of key biological events in morphogenesis.
Conclusion and outlook
Our study highlights how irregular cell shapes in epithelial monolayers naturally generate a spectrum of p-atic orders and their associated topological defects. By bridging cell-resolved data with continuum concepts, we show that multiple symmetries can coexist without strong correlations, suggesting that tissues are not restricted to a single symmetry class. This opens several exciting directions: investigating how higher-order defects couple to biological processes such as division, extrusion, or migration; testing whether even–odd asymmetries in defect statistics hold across different epithelial systems; and extending coarse-grained models to explicitly integrate multiple p simultaneously. More broadly, our approach demonstrates how concepts from soft condensed matter physics—symmetry, topology, and scale—can be leveraged to uncover hidden organizing principles in living matter.Author contributions
L. H.: investigation (equal), methodology (equal), software (equal), visualization (equal), writing – original draft, writing – review & editing (equal). G. O.: investigation (equal), methodology (equal), software (equal), visualization (equal), A. R., G. R. R.: investigation (support), software (support) V. G.: experimental setup (lead), segmentation (lead). A. D.: methodology (support), funding acquisition, writing – review & editing (equal). A. V.: conceptualization, investigation (support), methodology (support), supervision, funding acquisition, writing – review & editing (equal).Conflicts of interest
There are no conflicts to declare.Data availability
For all tasks we provide the considered Python code, see ref. 39.Appendix
Fig. 11–18 | ||
| Fig. 11 Raw experimental image from Frame 25, which was used in Fig. 4. | ||
 | ||
| Fig. 12 Raw experimental image from Frame 50, which was used in Fig. 4. | ||
 | ||
| Fig. 16 p-value of the Kolmogorov–Smirnov test reported in Fig. 13 (for defects obtained with a coarse-graining of ravg = 1.5rmax(t)). A low p-value (≤ 0.05) means that the difference between the two cumulative distribution functions compared with the Kolmogorov–Smirnov test is significant and a high p-value means that it is not possible to show a difference between the two distributions. To guide the eye we colored the background of the cells in red for values ≤ 0.05 and in blue for values > 0.05. | ||
 | ||
| Fig. 17 p-value of the Kolmogorov–Smirnov test reported in Fig. 14 (for defects obtained with a coarse-graining of ravg = 2.25rmax(t)). A low p-value (≤ 0.05) means that the difference between the two cumulative distribution functions compared with the Kolmogorov–Smirnov test is significant and a high p-value means that it is not possible to show a difference between the two distributions. To guide the eye we colored the background of the cells in red for values ≤ 0.05 and in blue for values > 0.05. | ||
 | ||
| Fig. 18 p-value of the Kolmogorov–Smirnov test reported in Fig. 15 (for defects obtained with a coarse-graining of ravg = 3.0rmax(t)). A low p-value (≤ 0.05) means that the difference between the two cumulative distribution functions compared with the Kolmogorov–Smirnov test is significant and a high p-value means that it is not possible to show a difference between the two distributions. To guide the eye we colored the background of the cells in red for values ≤ 0.05 and in blue for values > 0.05. | ||
Acknowledgements
We acknowledge fruitful discussions with Björn Böttcher, Brendan Tobin and Emma Happel. AD acknowledges funding from the Novo Nordisk Foundation (grant no. NNF18SA0035142 and NERD grant no. NNF21OC0068687), Villum Fonden (grant no. 29476), and the European Union (ERC, PhysCoMeT, 101041418). AV acknowledges funding from the German Research Foundation (Award FOR3013 “Vector- and tensor-valued surface PDEs”) and computing resources provided by JSC through MORPH and by ZIH through WIR.References
- G. Duclos, C. Erlenkämper, J.-F. Joanny and P. Silberzan, Nat. Phys., 2017, 13, 58–62 Search PubMed.
- T. B. Saw, A. Doostmohammadi, V. Nier, L. Kocgozlu, S. Thampi, Y. Toyama, P. Marcq, C. T. Lim, J. M. Yeomans and B. Ladoux, Nature, 2017, 544, 212–216 CrossRef CAS.
- K. Kawaguchi, R. Kageyama and M. Sano, Nature, 2017, 545, 327–331 CrossRef CAS PubMed.
- S. Monfared, G. Ravichandran, J. Andrade and A. Doostmohammadi, eLife, 2023, 12, e82435 Search PubMed.
- Y. Maroudas-Sacks, L. Garion, L. Shani-Zerbib, A. Livshits, E. Braun and K. Keren, Nat. Phys., 2021, 17, 251–259 Search PubMed.
- R. Alert, J. Casademunt and J.-F. Joanny, Ann. Rev. Condens. Matter Phys., 2022, 13, 143–170 Search PubMed.
- P. G. de Gennes and J. Prost, The physics of liquid crystals, Clarendon Press, Oxford, 2nd edn, 1993 Search PubMed.
- D. Cislo, F. Yang, H. Qin, A. Pavlopoulos, M. Bowick and S. Streichan, Nat. Phys., 2023, 19, 1201–1210 Search PubMed.
- Y.-W. Li and M. P. Ciamarra, Phys. Rev. Mater., 2018, 2, 045602 Search PubMed.
- M. Durand and J. Heu, Phys. Rev. Lett., 2019, 123, 188001 CrossRef CAS PubMed.
- A. Pasupalak, L. Yan-Wei, R. Ni and M. P. Ciamarra, Soft Matter, 2020, 16, 3914–3920 RSC.
- J.-M. Armengol-Collado, L. N. Carenza, J. Eckert, D. Krommydas and L. Giomi, Nat. Phys., 2023, 19, 1773–1779 Search PubMed.
- J. Eckert, B. Ladoux, R.-M. Mège, L. Giomi and T. Schmidt, Nat. Commun., 2023, 14, 5762 Search PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- B. I. Halperin and D. R. Nelson, Phys. Rev. Lett., 1978, 41, 121–124 CrossRef CAS.
- D. R. Nelson and B. I. Halperin, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2457–2484 CrossRef CAS.
- C. A. Murray and D. H. Van Winkle, Phys. Rev. Lett., 1987, 58, 1200–1203 Search PubMed.
- P. Bladon and D. Frenkel, Phys. Rev. Lett., 1995, 74, 2519–2522 Search PubMed.
- K. Zahn, R. Lenke and G. Maret, Phys. Rev. Lett., 1999, 82, 2721–2724 CrossRef CAS.
- U. Gasser, C. Eisenmann, G. Maret and P. Keim, ChemPhysChem, 2010, 11, 963–970 CrossRef CAS.
- E. P. Bernard and W. Krauth, Phys. Rev. Lett., 2011, 107, 155704 CrossRef PubMed.
- M. J. Bowick, O. V. Manyuhina and F. Serafin, Europhys. Lett., 2017, 117, 26001 CrossRef.
- K. W. Wojciechowski and D. Frenkel, Comput. Methods Sci. Technol., 2004, 10, 235–255 CrossRef.
- P.-Y. Wang and T. G. Mason, Nature, 2018, 561, 94–99 CrossRef CAS PubMed.
- T. Yu and T. G. Mason, J. Colloid Interface Sci., 2023, 665, 535–544 Search PubMed.
- D. Nelson and L. Peliti, J. Phys., 1987, 48, 1085–1092 CrossRef CAS.
- L. Giomi, J. Toner and N. Sarkar, Phys. Rev. E, 2022, 106, 024701 CrossRef CAS.
- L. Giomi, J. Toner and N. Sarkar, Phys. Rev. Lett., 2022, 129, 067801 Search PubMed.
- D. Krommydas, L. N. Carenza and L. Giomi, Phys. Rev. Lett., 2023, 130, 098101 CrossRef CAS PubMed.
- J.-M. Armengol-Collado, L. N. Carenza and L. Giomi, eLife, 2024, 13, e86400 CrossRef CAS PubMed.
- L. Happel, G. Oberschelp, V. Grudtsyna, H. P. Jain, R. Sknepnek, A. Doostmohammadi and A. Voigt, eLife, 2025, 14, RP105680 CrossRef.
- B. Loewe, M. Chiang, D. Marenduzzo and M. Marchetti, Phys. Rev. Lett., 2020, 125, 038003 Search PubMed.
- N. Ray, B. Vallet, W. C. Li and B. Lévy, ACM Trans. Graphics, 2008, 27, 10 Search PubMed.
- J. Palacios and E. Zhang, ACM Trans. Graphics, 2007, 26, 55–es CrossRef.
- J. Palacios and E. Zhang, IEEE Trans. Visualization Comput. Graphics, 2011, 17, 947–955 Search PubMed.
- D. Wenzel, M. Nestler, S. Reuther, M. Simon and A. Voigt, Comput. Methods Appl. Math., 2021, 21, 683–692 Search PubMed.
- V. Skogvoll, J. Rønning, M. Salvalaglio and L. Angheluta, npj Comput. Mater., 2023, 9, 122 Search PubMed.
- R. Alert and X. Trepat, Annu. Rev. Condens. Matter Phys., 2020, 11, 77–101 CrossRef.
- G. Oberschelp, A. Richter, G. R. Rode and L. Happel, Zenodo DOI:10.5281/zenodo.18175147.
- S. van der Walt, J. L. Schönberger, J. Nunez-Iglesias, F. Boulogne, J. D. Warner, N. Yager, E. Gouillart, T. Yu and the scikit-image contributors, PeerJ, 2014, 2, e453 Search PubMed.
- A. J. Vromans and L. Giomi, Soft Matter, 2016, 12, 6490–6495 RSC.
- D. Wenzel and A. Voigt, Phys. Rev. E, 2021, 184, 054410 CrossRef.
- W. Schroeder, K. Martin and B. Lorensen, The Visualization Toolkit, Kitware, 4th edn, 2006 Search PubMed.
- R. Laramee, B. Jobard and H. Hauser, IEEE Visualization, 2003. VIS 2003., 2003, pp. 131–138 Search PubMed.
- R. F. Laine, K. L. Tosheva, N. Gustafsson, R. D. M. Gray, P. Almada, D. Albrecht, G. T. Risa, F. Hurtig, A.-C. Lindås, B. Baum, J. Mercer, C. Leterrier, P. M. Pereira, S. Culley and R. Henriques, J. Phys. D: Appl. Phys., 2019, 52, 163001 CrossRef CAS PubMed.
- J. W. Pylvänäinen, R. F. Laine, B. M. Saraiva, S. Ghimire, G. Follain, R. Henriques and G. Jacquemet, J. Cell Sci., 2023, 136, jcs260728 CrossRef.
- C. Stringer, T. Wang, M. Michaelos and M. Pachitariu, Nat. Methods, 2021, 18, 100–106 CrossRef CAS.
- J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS.
- M. Chiang, A. Hopkins, B. Loewe, M. C. Marchetti and D. Marenduzzo, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2319310121 CrossRef CAS.
- J. Zhang, C. W. Chan, B. Li and R. Zhang, arXiv, 2025, preprint, arXiv:2506.04068 DOI:10.48550/arXiv.2506.04068.
| This journal is © The Royal Society of Chemistry 2026 |